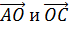- Ваш ответ
- решение вопроса
- Похожие вопросы
- Тест «Понятие вектора»
- Просмотр содержимого документа «Тест «Понятие вектора»»
- Треугольник. Медиана, биссектриса, высота, средняя линия.
- теория по математике 📈 планиметрия
- Виды треугольников по углам
- Виды треугольников по сторонам
- Медиана, биссектриса, высота, средняя линия треугольника
- Медиана
- Биссектриса
- Высота
- Средняя линия
- 📽️ Видео
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Ваш ответ
Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

решение вопроса
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,997
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Тест «Понятие вектора»
Просмотр содержимого документа
«Тест «Понятие вектора»»
Тест «Понятие вектора»
З 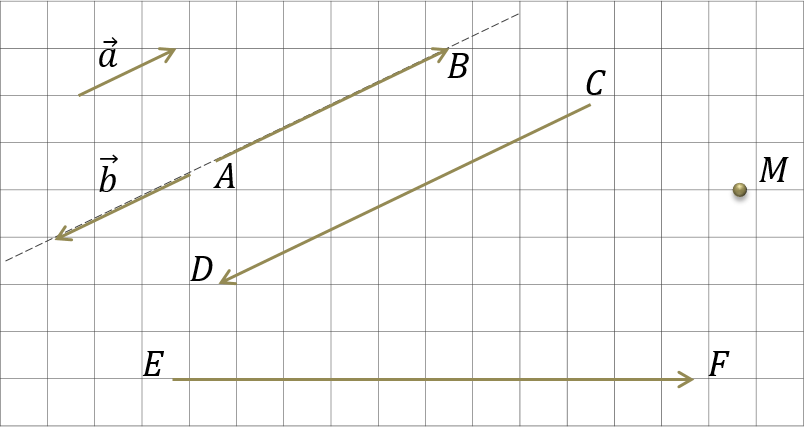
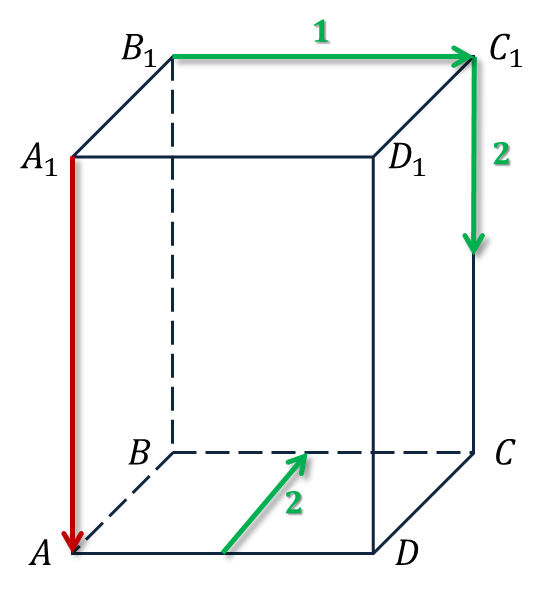
Пользуясь данными рисунка, укажите векторы сонаправленные вектору 
Выберите несколько из 5 вариантов ответа:
1) 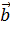
3) 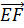
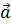
Укажите номер вектора, который коллинеарен вектору AA1.
Д 
Выберите один из 4 вариантов ответа:
1) 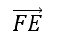
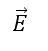

Пользуясь данными рисунка, укажите вектор, длина которого равна 4 см.
Выберите один из 4 вариантов ответа:
1) 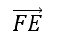
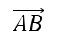

В 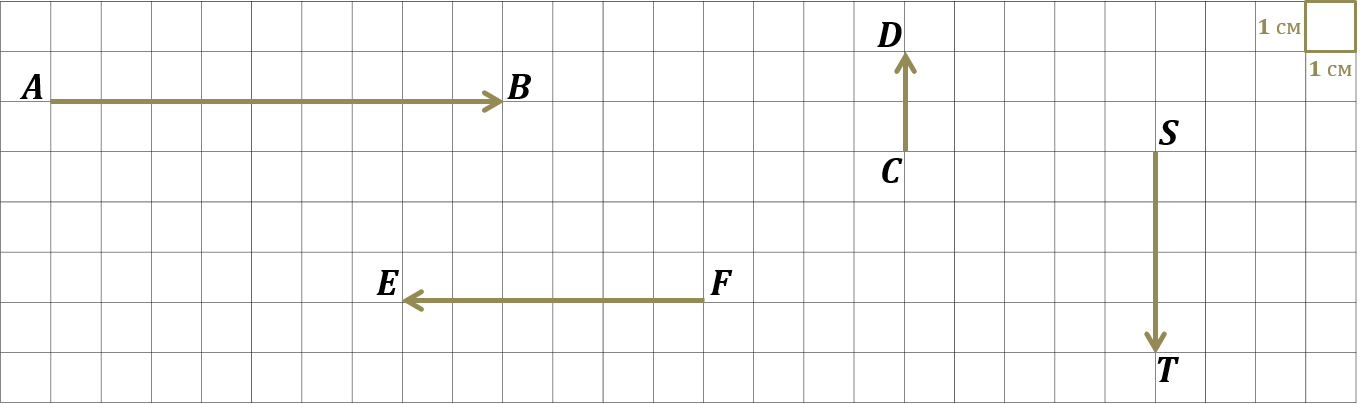
Определите сумму длин всех векторов, изображённых на рисунке. В ответе укажите только числовое значение результата без единиц измерения.
З 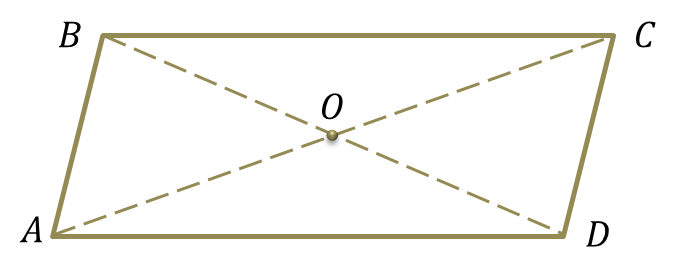
Пользуясь данными рисунка и тем, что ABCD — параллелограмм, укажите пары равных векторов.
Выберите несколько из 4 вариантов ответа:
1) 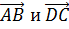
3) 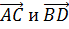
З 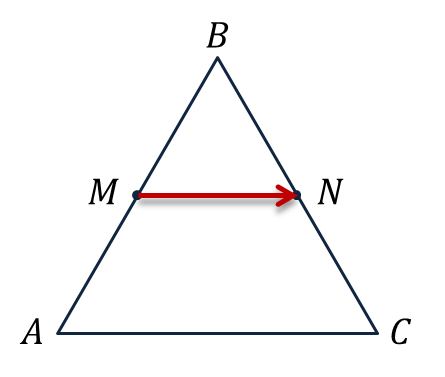
MN — средняя линия равностороннего треугольника ABC, со стороной равной 22 сантиметра.
Найдите длину вектора 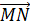
Продолжите фразу. «Все векторы, изображённые на рисунке являются . .»
Выберите один из 4 вариантов ответа:
2) противоположно направленными
Какие условия должны выполняться, чтобы векторы 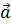
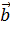
Выберите несколько из 4 вариантов ответа:
Пользуясь данными рисунка, вычислите длину стороны квадрата. В ответе укажите только число.
Видео:№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать

Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
| Остроугольные | Тупоугольные | Прямоугольные |
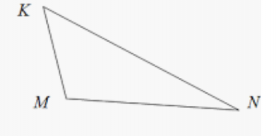
| Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС. | Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой. | Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный. |
 |  |  |
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .
Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .
Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
📽️ Видео
Средняя линия. Теорема о средней линии треугольникаСкачать

Средняя линия треугольника – 8 класс геометрияСкачать

Задача, которую боятсяСкачать

61. Геометрия на ЕГЭ по математике. Задачи на тему "Векторы"Скачать

МАТЕМАТИКА | Средняя линия треугольникаСкачать

ВЕКТОРЫ решение задач 9 класс АтанасянСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Сложение векторов. 9 класс.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

ЕГЭ 2024 Ященко 5 вариант ФИПИ школе полный разбор!Скачать

Средняя линия треугольника. Задачи по готовым чертежамСкачать

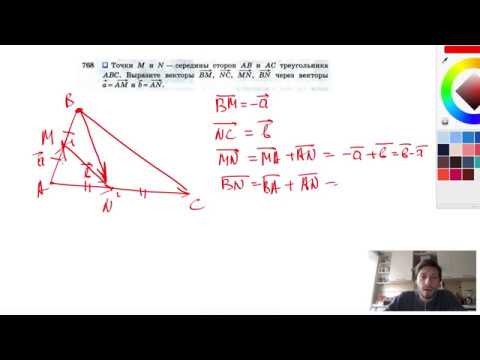
№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать