Высота тупоугольного треугольника циркулем

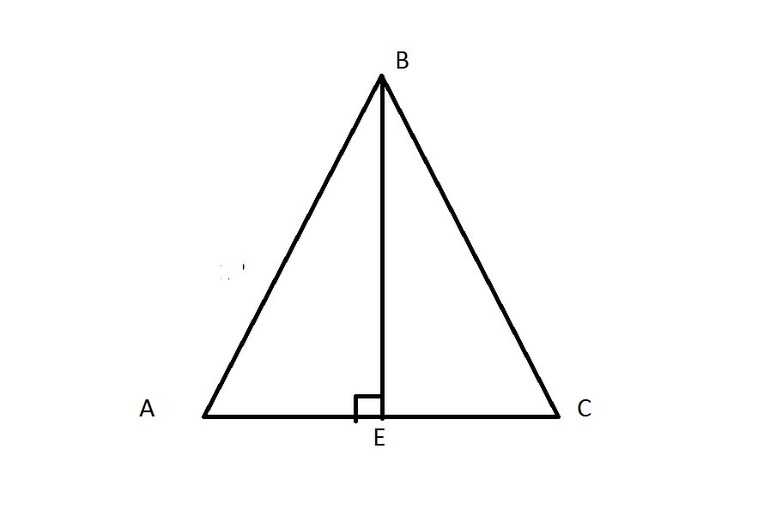
Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.

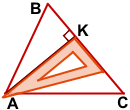
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.

AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.

BF⊥AC.

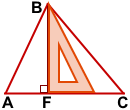
BF — высота треугольника ABC, опущенная из вершины B на сторону AC.

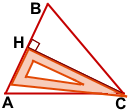
CH — высота треугольника ABC, проведённая из вершины C к стороне AB.

Все высоты треугольника пересекаются в одной точке.

В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

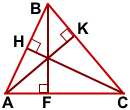
Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.

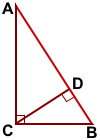
В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.

Угольник прикладываем прямым углом так, чтобы одна сторона проходила через гипотенузу, а другая — через прямой угол.

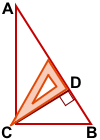
CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.

Точка пересечения высот прямоугольного треугольника — вершина прямого угла.

Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.

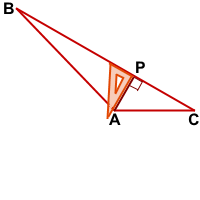
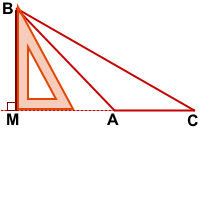
В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.

Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.

AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.

Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.

Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.

Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.

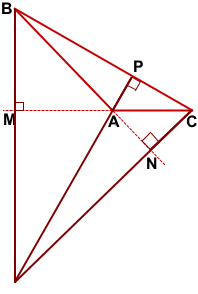
BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.

CN⊥AB,

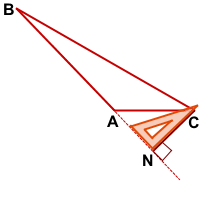
CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.

Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.

Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.

Мы рассмотрели, как строить высоты треугольника с помощью угольника.

Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».

Видео:Построение высоты в треугольникеСкачать

Как построить высоту треугольника — основные способы

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

С применением циркуля

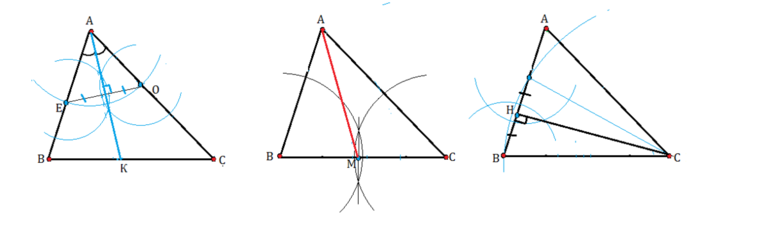
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.

Способ начертить искомый отрезок:

• На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
• Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
• Иглу циркуля ставят в вершине любого угла у основания.
• Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
• Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
• Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
• Делают пометку в месте пересечения начерченных окружностей.
• Ластиком стирают лишние линии, оставляя лишь поставленную точку.
• С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
• Стирают линии, находящиеся под основанием.

Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.

Видео:Построение медианы в треугольникеСкачать

С помощью линейки

Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.

В остроугольном треугольнике

Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.

Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.

Правильная последовательность действий:

• Находят вершину, из которой хотят провести перпендикуляр.
• Совмещают угольник с противоположной стороной фигуры.
• Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
• Простым карандашом проводят линию, которая и будет искомым отрезком.

В тупоугольной фигуре

Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.

Порядок действий:

• Располагают чертёж так, чтобы тупой угол оказался у основания.
• Угольник прикладывают к наибольшей стороне фигуры.
• Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
• Соединяют 2 точки простым карандашом, получая искомую линию.

В прямоугольном и равнобедренном

В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.

Пошаговая инструкция:

• Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
• Вторую сторону линейки совмещают с вершиной прямого угла.
• Проводят линию, которая будет высотой.

Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.

Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:

• Линейкой замеряют длину основания.
• Эту величину делят на 2.
• Полученное значение откладывают от вершины одного из углов при основании.
• Отмечают середину стороны и соединяют её с верхней точкой фигуры.

Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.

Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.

Видео:Высота медиана биссектриса в тупоугольном треугольникеСкачать

Высота треугольника

Расстояние между вершиной треугольника и противоположной стороной называется высотой. Формально, это самый короткий отрезок между вершиной треугольника и (с возможным продлением) противоположной стороной.

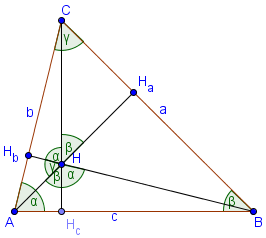
Каждый треугольник имеет 3 высоты которые пересекаются в одной точке — ортоцентре. Если мы используем стандартные обозначения, в треугольнике ABC , есть три высоты: AH_a, BH_b, CH_c . Эти три отрезка пересекаются в одной точке — ортоцентре (точка H на рисунке) треугольника. Для тупого треугольника (имеющего один угол, больше чем 90°), ортоцентр находится за пределами треугольника.

Высоты остроугольного треугольника

Ортоцентр — это точка внутри треугольника.

∠ AHB = 180 — γ = α + β
∠ BHC = 180 — α = β + γ
∠ AHC = 180 — β = α + γ
∠ AHH_c = β, ∠ BHH_c = α, ∠ BHH_a = γ

Высоты тупоугольного треугольника

Ортоцентр находится вне треугольнка.
Две высоты также всегда лежат вне треугольника.
∠ AHH_c = ∠ CBA = β
∠ H_cHB = ∠ CAB = α

Правый треугольник

Высота AH_a совпадает с AC.
Высота BH_b совпадает с BC.
Ортоцентр H совпадает с C.
∠ ACH_c = β, ∠ BCH_c =α

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Формулы

R — радиус описанной окружности
r — радиус вписанной окружности
p — полуперимерт: (a + b + c)/2

🔥 Видео

№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Высоты треугольника.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Точка пересечения высот треугольника.Скачать

Построение биссектрисы в треугольникеСкачать

ПОСТРОЕНИЕ ВЫСОТЫ ТРЕУГОЛЬНИКА С ПОМОЩЬЮ ЦИРКУЛЯ. ЗАДАЧИ НА ПОСТРОЕНИЕ | ГЕОМЕТРИЯ 7 классСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

Построение биссектрисы угла. 7 класс.Скачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Как построить все высоты в тупоугольном треугольнике #shortsСкачать

Построение высоты равнобедренного треугольника с помощью циркуля и линейкиСкачать

Треугольник, построение высоты.Скачать

Как построить высоту в треугольнике?Скачать