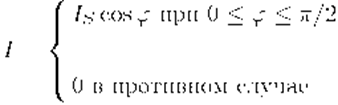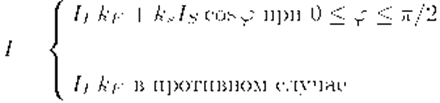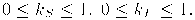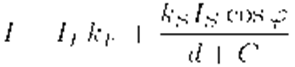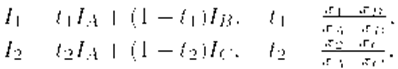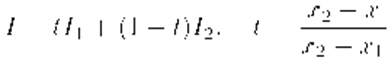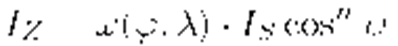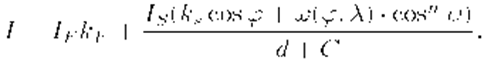Методы закраски поверхностей трехмерных объектов расчет координат вектора нормали (8 видео)

Методы закраски поверхностей трехмерных объектов расчет координат вектора нормали

Методы закраски граней

В настоящее время в большинстве программ трёхмерного моделирования, таких как 3D Studio MAX и им подобных, вся сцена задаётся набором треугольников (граней), для которых рассчитывается значение освещённости и накладываются текстуры. Для рисования граней с наложенной на них освещённостью используются следующие три метода: метод постоянной закраски, метод Гуро и метод Фонга.

Метод постоянной закраски

Пусть имеется грань, заданная тремя вершинами и вектором нормали n. Метод заключается в том, что освещённость рассчитывается целиком для всей грани, и цветом, соответствующим этой освещённости, рисуется вся грань целиком. Освещённость в данном случае представляется в цветовой модели RGB и является трёхмерным вектором с положительным значением координат. В качестве простейшей модели освещённости в этом случае может использоваться следующая модель:

I = K a · I a + K d · I d · (n, l), где
I — рассчитываемое значение освещённости грани;
K a — коэффициент постоянной освещённости (независящей от характеристик сцены и источников цвета);
I a — значение постоянной освещённости;
K d — коэффициент диффузной освещённости (освещённость, которая зависит лишь от материала (цвета) объекта и от доли площади объекта, видимой наблюдателем);
I d — цвет грани;
n — вектор нормали к грани;
l — направление на источник света.

Эта формула может быть модифицированна с учётом всех источников света, воздействующих на конкретную грань. При этом второе слагаемое формулы будет являться суммой, учитывающей влияние нескольких источников света.

После расчёта значения освещённости может оказаться, что освещённость не является единичным вектором или что значения некоторых координат вектора освещённости приняли отрицательные значения. В этом случае выполняется следующая нормировка: для каждой координаты вектора освещённости проверяется её значение и если оно больше 1, то выполняется присваивание значению этой координаты 1; если это значение меньше 0, то выполняется присваивание значению этой координаты 0.

После того, как вычислена освещённость грани, производится растеризация грани в соответствии с используемым перспективным преобразованием, и производится вывод пикселей цветом, соответствующим вычисленному значению освещённости.

Метод постоянной закраски прост, но имеет один существенный недостаток — модель, построенная с применением этого метода визуально носит чисто полигональный характер — не вооружённым глазом заметно, что модель состоит из отдельных граней. Другими словами, освещённость в этом случае является кусочно-постоянной функцией с конечным числом точек разрыва первого рода.

Метод Гуро

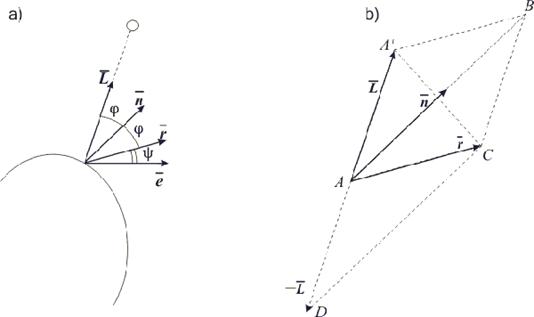
Данный метод обеспечивает некоторую сглаженность освещённости в пределах одной грани и визуально смотрится лучше метода постоянной закраски при несущественном увеличении сложности вычислений. Для реализации метода освещённость вычисляется для каждой вершины грани, используя, например, модель освещённости, описанную в методе постоянной закраски. Для вычисления значения каждого пикселя грани используется билинейная интерполяция: значение освещённости сначала интерполируется по рёбрам грани, а затем между рёбрами грани.

Методы закраски поверхностей трехмерных объектов расчет координат вектора нормали

Рис. 1

Пусть требуется вычислить значение освещённости в точке A (рис. 1). Пусть вершине v 1 соответствует значение освещённости I 1 , а вершине v 2 — значение освещённости I 2 . Обозначим искомую освещённость в точке A через I A . Тогда значение освещённости в точке A вычисляется по следующей формуле:

I A = I 1 + (I 2 — I 1 ) · (A — v 1 ) / (v 2 — v 1 )

Если для этой формулы записать рекуррентное соотношение с учётом растеризации грани на плоскость проектирования, то вычисления значения освещённости можно значительно сократить, используя инкрементальные методы:

I A+1 = I A + C, C = (I 2 — I 1 ) / N, где
I A+1 — значение освещённости в точке, следующей после точки A по вертикали;
N — значение, которое вычисляется после выполнения перспективного преобразования по отношению к вершинам v 1 и v 2 как модуль разности между вертикальными координатами (Y) векторов v 2 и v 1 .

Для вычисления освещённости в точке C используется точно такая же формула, но вместо вершин v 1 и v 2 используются координаты точек A и B, а вместо значений освещённостей I 1 и I 2 используются значения освещённостей в точках A и B.

Такой подход позволяет получить плавное изменение значения освещённости в пределах одной грани. Однако, метод Гуро имеет тот недостаток, что на границах граней значение освещённости терпит разрыв и визуально не обеспечивается плавного изменения значения освещённости на границах граней. Ещё одним недостатком метода Гуро является то, что освещённость грани зависит от ориентации грани по отношению к наблюдателю, т. е. метод не учитывает поворот грани относительно направления на наблюдателя, так как интерполяция производится в пределах строки. Но не смотря на это, метод Гуро прост в реализации и для вычисления значения освещённости каждого пикселя требуется только одно сложение. Результат применения метода Гуро для заливки граней приведён на рис. 2.

Рис. 2

Метод Фонга

Для построения модели с гладкой функцией освещённости требуется, чтобы для этой модели было задано непрерывное поле единичных векторов нормали, но, так как модель состоит из граней, такое поле не может быть задано явным образом. Однако, это поле можно искуственно смоделировать, опираясь на нормали к каждой грани. Суть метода Фонга состоит в том, что для каждой точки грани вычисляется значение вектора нормали, используя билинейную интерполяцию. Таким образом, в методе Фонга интерполируются значения векторов нормалей, а не значения освещённостей, как в методе Гуро. Для реализации метода Фонга требуется иметь значения векторов нормалей для каждой вершины грани. Для вычисления значения вектора нормали n для произвольной вершины может использоваться следующая формула:

n = (n 1 + n 2 + . + n k ) / || n 1 + n 2 + . + n k ||, где nk — значение вектора нормали к k-й грани, которой принадлежит вершина с вычисляемой нормалью n.

После того, как вычислено значение нормали для конкретной точки грани, можно вычислить освещённость для этой точки, используя, например, модель освещённости, описанную в методе постоянной закраски.

Метод Фонга требует гораздо больше вычислений для каждого пикселя, чем метод Гуро (три сложения на пиксель), однако обеспечивает значительно лучшее качество изображения по сравнению с методом Гуро. Метод Фонга также устраняет недостаток метода Гуро — зависимость освещённости грани от её положения относительно наблюдателя. Результат применения метода Фонга для заливки граней приведён на рис. 3.

Содержание

Закраска граней: плоское закрашивание (Ламберта)
Закраска методом Гуро
Модель Фонга
16 Методы Гуро и Фонга для закрашивания
Рекомендуемые файлы
📽️ Видео

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Закраска граней: плоское закрашивание (Ламберта)

Объекты окружающего пространства становятся видимыми для глаза благодаря световой энергии, которая может излучаться поверхностью предмета, отражаться или проходить сквозь нее. В свою очередь, отражение света от поверхности зависит от физических свойств материала, из которого она изготовлена, а также от характера и расположения источника света. Яркость (или интенсивность) освещения зависит от энергии светового потока, которая обуславливается, во-первых, мощностью источника света, а во-вторых, отражающими и пропускающими свойствами объекта.

Сначала мы рассмотрим модель освещения, учитывающую только отражение. Свойства отраженного света зависят главным образом от направления лучей и характеристик отражающей поверхности.

Отражение может быть двух видов: диффузное и зеркальное. Первое из них возникает в ситуации, когда свет как бы проникает под поверхность объекта, поглощается, а потом равномерно излучается во всех направлениях. Поверхность в этом случае рассматривается как идеальный рассеиватель . При этом возникает эффект матового света, а видимая освещенность того или иного участка поверхности не зависит от положения наблюдателя. Зеркальное отражение, наоборот, происходит от внешней поверхности, интенсивность его неоднородна, поэтому видимый максимум освещенности зависит от положения глаза наблюдателя.

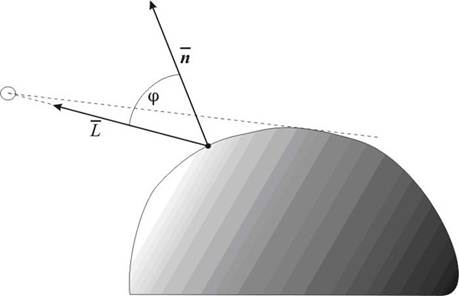
Рис. 10.1. Освещение точечным источником

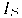
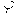
Свет точечного источника отражается от поверхности рассеивателя по закону Ламберта: интенсивность отражения пропорциональна косинусу угла между внешней нормалью к поверхности и направлением к источнику света Е сли — интенсивность источника света, — угол между вектором внешней нормали к поверхности и направлением к источнику света, то интенсивность отраженного света определяется формулой

При таком расчете интенсивности получится очень контрастная картина, т.к. участки поверхности, на которые лучи от источника не попадают напрямую, останутся абсолютно черными. Для повышения реалистичности необходимо учитывать рассеивание света в окружающем пространстве. Поэтому вводится фоновая освещенность, зависящая от интенсивности рассеянного света , и интенсивность отраженного света определяется выражением

где — коэффициент диффузного отражения рассеянного света, — коэффициент диффузного отражения падающего света,

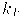
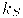
В описанной модели пока никак не учитывалась удаленность источника света от поверхности, поэтому по освещенности двух объектов нельзя судить об их взаимном расположении в пространстве. Если мы хотим получить перспективное изображение, то необходимо включить затухание интенсивности с расстоянием. Обычно интенсивность света обратно пропорциональна квадрату расстояния от источника. В качестве расстояния до источника в случае перспективного преобразования можно взять расстояние до центра проекции, и если он достаточно удален, то изображение будет достаточно адекватным. Но если этот центр расположен близко к объекту, то квадрат расстояния меняется очень быстро, и в этом случае лучше использовать линейное затухание. В этом случае интенсивность отраженного света от непосредственно освещенных участков поверхности будет задаваться формулой

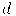
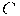
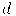
где — расстояние до центра проекции, а — произвольная постоянная. Если центр проекции находится на бесконечности, т. е. при параллельном проецировании, то в качестве можно взять расстояние до объекта, наиболее близкого к наблюдателю.

В отличие от диффузного , зеркальное отражение является направленным. Идеальное зеркало отражает лучи по принципу «отраженный и падающий лучи лежат в одной плоскости, причем угол падения равен углу отражения» (имеется в виду угол между направлением луча и нормалью к поверхности). Если поверхность не идеально зеркальная, то лучи отражаются в различных направлениях, но с разной интенсивностью, а функция изменения интенсивности имеет четко выраженный максимум.

Рис. 10.2. Зеркальное отражение

Вместе с тем, выделяют три относительно простых метода затенения (закрашивания), предполагающие ту или иную интерполяцию освещенности: метод постоянного закрашивания (по Ламберту), метод Гуро и метод Фонга .

Независимо от применяемого в дальнейшем метода поверхности объектов аппроксимируются набором плоских выпуклых граней – полигонов. Чаще всего, для этой цели используются треугольные полигоны. Это объясняется тем, что три вершины однозначно определяют положение плоскости в пространстве и, кроме того, из треугольников всегда можно получить любой другой многоугольник.

Суть метода постоянного закрашивания (по Ламберту) заключается в том, что на каждом полигоне определяется освещенность в произвольной точке, и полученное значение используется для всего полигона. Изображение при этом имеет ярко выраженный полигональный характер – видно, что поверхность состоит из отдельных граней, на границах между которыми освещенность претерпевает разрывы (фактически освещенность является кусочно-постоянной функцией).

Метод Гуро обеспечивает непрерывность освещенности за счет ее билинейной интерполяции: после определения значений освещенности в вершинах полигона применяют линейную интерполяцию вдоль сторон полигона, а потом – линейную интерполяцию между сторонами полигона вдоль каждой из сканирующих строк, пересекающих полигон (при этом освещенность рассчитывается для каждого пикселя соответствующего интервала сканирующей строки).

В методе Фонга также применяется билинейная интерполяция, но по отношению к вектору нормали к поверхности: рассчитывают векторы нормали в вершинах полигона, осуществляют линейную интерполяцию вектора нормали вдоль сторон полигона, а затем – линейную интерполяцию вдоль каждой сканирующей строки, пересекающей полигон, между сторонами полигона (при этом вектор нормали рассчитывается для каждого пикселя соответствующего интервала сканирующей строки). Полученное поле распределения вектора нормали используется в дальнейшем при расчете освещенности для каждого пикселя полигона (отметим здесь, что ориентация друг относительно друга вектора нормали к поверхности и направления света от точечного источника учитывается во всех моделях освещенности).

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Закраска методом Гуро

Один из способов устранения дискретности интенсивностей закрашивания был предложен Гуро . Его метод заключается в том, что используются не нормали к плоским граням, а нормали к аппроксимируемой поверхности, построенные в вершинах многогранника. После этого вычисляются интенсивности в вершинах, а затем во всех внутренних точках многоугольника выполняется билинейная интерполяция интенсивности.

Метод сочетается с алгоритмом построчного сканирования. После того как грань отображена на плоскость изображения, для каждой сканирующей строки определяются ее точки пересечения с ребрами. В этих точках интенсивность вычисляется с помощью линейной интерполяции интенсивностей в вершинах ребра. Затем для всех внутренних точек многоугольника, лежащих на сканирующей строке ,т акже вычисляется интенсивность методом линейной интерполяции двух полученных значений.

Рис. 10.3. Интерполяция интенсивности

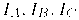
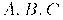
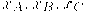
Пусть — интенсивности в вершинах , — горизонтальные координаты этих точек. Тогда в точках пересечения сканирующей строки с ребрами многоугольника интенсивности можно вычислить по формулам интерполяции:

После этого интенсивность в точке х получаем путем интерполяции значений на концах отрезка:

К недостаткам метода Гуро следует отнести то, что он хорошо работает только с диффузной моделью отражения. Форма бликов на поверхности и их расположение не могут быть адекватно воспроизведены при интерполяции на многоугольниках. Кроме того, есть проблема построения нормалей к поверхности. В алгоритме Гуро нормаль в вершине многогранника вычисляется путем усреднения нормалей к граням, примыкающим к этой вершине. Такое построение сильно зависит от характера разбиения.

Видео:Координаты вектора. 9 класс.Скачать

Модель Фонга

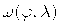
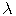
где — функция отражения, — длина волны. Степень, в которую возводится косинус угла, влияет на размеры светового блика, наблюдаемого зрителем. Графики этой функции являются характерными кривыми поведения функции изменения интенсивности в зависимости от свойств поверхности.

Рис. 10.4. Зеркальное отражение

Теперь модель освещенности, учитывающую зеркальное и диффузное отражения, можно описать формулой

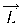
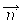
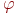
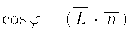
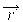
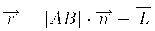
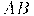
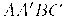
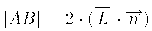
Используя единичные векторы (направление к источнику) и (внешняя нормаль), косинус угла можно вычислить через скалярное произведение: . Для расчета интенсивности зеркального отражения сначала надо определить отраженный вектор . Из рис. 11.2 видно, что . С другой стороны является диагональю ромба , поэтому . Учитывая все эти соотношения, получаем формулу

В алгоритмах закрашивания с использованием цветовых моделей интенсивность рассчитывается для каждого из базовых цветов, поскольку изменение интенсивности при зеркальном отражении зависит от длины волны. Фонг предложил вместо интерполяции интенсивностей произвести интерполяцию вектора нормали к поверхности на сканирующей строке. Этот метод требует больших вычислительных затрат, поскольку формулы интерполяции применяются к трем компонентам вектора нормали, но зато дает лучшую аппроксимацию кривизны поверхности. Поэтому зеркальные свойства поверхности воспроизводятся гораздо лучше.

Нормали к поверхности в вершинах многогранника вычисляются так же, как и в методе Гуро . А затем выполняется билинейная интерполяция в сочетании с построчным сканированием. После построения вектора нормали в очередной точке вычисляется интенсивность.

Этот метод позволяет устранить ряд недостатков метода Гуро , но не все. В частности, эффект полос Маха в отдельных случаях в методе Фонга бывает даже сильнее, хотя в подавляющем большинстве случаев аппроксимация Фонга дает лучшие результаты.

В приложении 1 реализуются все три метода затенения при освещении трехмерного объекта двумя источниками. Работу программы иллюстрирует экранное окно, в котором представлена одна и та же фигура. Способ закраски и расположение источников выбираются с помощью инструментов.

В приложении 2 реализуются так же все три метода затенения при освещении различных объектов точечным источником. Работу программы иллюстрирует экранное окно, в котором представлены различные фигуры. Фигуры следует выбирать из папки VRP, которую необходимо скопировать на свой компьютер, разархивировать и указать к ней путь при открытии. Способ закраски выбор фигуры и расположение источника выбираются с помощью инструментов.

Видео:9 класс, 2 урок, Координаты вектораСкачать

16 Методы Гуро и Фонга для закрашивания

Методы Гуро и Фонга для закрашивания
поверхностей. Методы прямой и обратной
трассировки лучей

Рассмотрим методы закрашивания объектов, моделируемых многогранниками и полигональными сетками. Они основаны на моделях отражения света.

Зеркальное отражение. Угол между нормалью и падающим лучом равен углу между нормалью и отраженным лучом. Оба луча и нормаль располагаются в одной плоскости (рис. 27).

Поверхность считается идеально зеркальной, если на ней отсутствуют какие-либо неровности, шероховатости. Собственного цвета такая поверхность не имеет. Световая энергия падающего

Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны: чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.

При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов падения луча, близких к 90°.

Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Рекомендуемые файлы

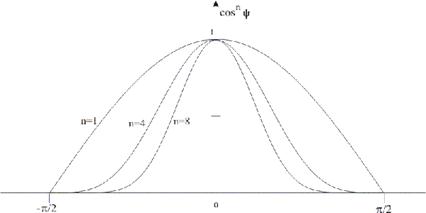
Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемых по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cos a) p , где a – угол отклонения от линии идеально отраженного луча. Показатель p находится в диапазоне от 1 до 200 и зависит от качества полировки. Соотношение можно записать следующим образом:

где I – интенсивность излучения источника; K_s – коэффициент пропорциональности.

Диффузное отражение. Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны.

Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности:

где I – интенсивность источника света; K_d – коэффициент, который учитывает свойства материала поверхности. Значение K_d находится в диапазоне от 0 до 1.

Интенсивность отраженного света не зависит от расположения наблюдателя.

Матовая поверхность имеет свой цвет. Наблюдаемый цвет определяется комбинацией собственного цвета поверхности и цвета излучения источника света.

Поскольку в природе не существует идеально зеркальных или полностью матовых поверхностей, то при изображении объектов средствами КГ обычно моделируют сочетание зеркального и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузного и зеркального компонентов:

где константы K_d, K_s определяют отражательные свойства материала.

Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов q и a. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:

где I_a – интенсивность рассеянного света, K_a – константа, определяющая рассеиваюшие свойства поверхности.

Следует учесть тот факт, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использования такого правила вызывает определенные сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой

где R – расстояние от центра проекции до поверхности, k – константа, подбираемая эмпирически.

Определение цвета закрашивания точек объектов в соответствии с описанной моделью. Наиболее просто выполняется расчет в градациях серого цвета (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости.

Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонентов. Коэффициенты K_a и K_d различны – они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент K_s будет одинаковым для всех компонентов цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонентов.

Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можно замаскировать за счет увеличения числа граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней – такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить число граней, что приводит к существенному замедлению визуализации – чем больше граней, тем меньше скорость рисования объектов.

Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяции цветов примыкающих граней.

Закрашивание граней по методу Гуро осуществляется в четыре этапа.

1. Вычисляются нормали к каждой грани.

2. Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 28).

3. На основе нормалей в вершинах вычисляются значения интенсивности в вершинах согласно выбранной модели отражения света.

4. Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.

Вектор нормали в вершине (a) равен: N_a = (N₁ + N₂ + N₃) / 3.

Интерполированные значения интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно определять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис. 29).

Интерполированная интенсивность I в точке (X, Y) определяется исходя из пропорции

Значения интенсивностей I₁ и I₂ на концах горизонтального отрезка представляют собой интерполяцию интенсивности в вершинах:

Метод Фонга аналогичен методу Гуро, но при его использовании для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей (рис. 30).

1. Определяются нормали к граням.

2. По нормалям к граням определяются нормали в вершинах.

3. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали.

4. По направлению векторов нормали определяется цвет точек грани в соответствии с выбранной моделью отражения света.

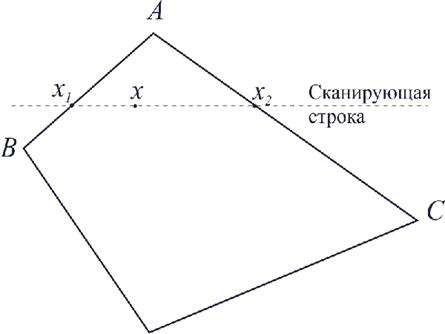
Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N’_a, N’_b и N’_c, исходящими из центра координат плоскости проецирования и параллельными соответствующим нормалям N_a, N_b и N_c в вершинах a, b и c.

Теперь найдем координаты вектора N’:

Вектор N’ параллелен вектору N для нормали в точке (X, Y), поэтому его можно использовать для расчета отражения света так же, как и вектор нормали N.

Метод Фонга сложнее метода Гуро. Для каждой точки (пиксела) поверхности необходимо выполнять намного больше вычислительных операций (рис. 31). Тем не менее он дает значительно лучшие результаты, в особенности при имитации зеркаль

Методы трассировки лучей

Прямая трассировка. В методе прямой трассировки генерируется пучок лучей, выходящих из источника во всевозможных направлениях.

Большинство лучей, испущенных источником, не попадает в приемник, а значит, и не влияет на формируемое в нем изображение. Лишь очень малая часть лучей после всех отражений и преломлений в конце концов попадает в приемник, создавая изображение сцены в его рецепторах. На шероховатых поверхностях возникает множество диффузно отраженных лучей. Все их нужно программно генерировать и отслеживать, что лавинообразно усложняет задачу трассировки.

Прохождение луча в неидеальной среде сопровождается рассеянием и поглощением световой энергии на ее микрочастицах. Эти физические процессы чрезвычайно трудно адекватно моделировать на ЭВМ с ее конечными вычислительными ресурсами. На практике ограничиваются применением коэффициента затухания энергии луча на единицу пройденного им расстояния. Аналогично вводятся коэффициенты уменьшения энергии луча при его отражении и преломлении на поверхности раздела сред. С учетом этих коэффициентов отслеживается уменьшение энергии всех первичных и вторичных лучей в процессе их блуждания в пространстве сцены. Как только энергия некоторого луча становится меньше заданного абсолютного уровня или уменьшается в заданное число раз, трассировка данного луча прекращается.

Таким образом, главными недостатками метода прямой трассировки являются его большая трудоемкость и малая эффективность. При реализации метода большая часть работы по расчету пересечений лучей с объектами оказывается проделанной впустую.

Обратная трассировка. Метод обратной трассировки разработан в 80-х годах. Основополагающими считаются работы Уиттеда и Кея.

Для отсекания лучей, не попавших в приемник, достаточно рассматривать наблюдателя в качестве источника обратных лучей. Первичным лучом будет считаться луч V от наблюдателя к какой-либо точке на поверхности объекта.

По рассмотренным выше методикам рассчитываются вторичные, третичные и т.д. лучи. В результате для каждого первичного луча строится дерево трассировки, ветви которого составляют вторичные лучи. Ветвление трассы заканчивается, если:

● луч выходит за пределы сцены,

● луч встречается с непрозрачным телом, поглощающим свет,

● луч попадает в источник света,

● интенсивность луча падает ниже порога чувствительности,

● число расщеплений первичного луча становится слишком большим для имеющихся машинных ресурсов.

Результирующая прямая световая энергия (цвет и интенсивность), попавшая в приемник из направления V, слагается из энергий терминальных вершин дерева с учетом их потерь при распространении в оптических средах.

Метод обратной трассировки фактически аккумулирует все лучи, в действительности приходящие в приемник из определенного направления независимо от их начала. Это позволяет видеть и изображать на экране:

● непрозрачные объекты, поглощающие обратные лучи;

● прозрачные объекты, через которые благодаря преломлению наблюдателю видны другие объекты;

● отражения объектов на зеркальных поверхностях, в том числе и блики, соответствующие попаданию обратных лучей в источник света;

● тени, образующиеся в точках поверхности, заслоненных от источника другими объектами;

● другие разнообразные оптические эффекты.

Количество «зондирующих» обратных лучей, подвергаемых трассировке, ограничено числом точек на поверхностях объектов сцены, видимых из точки расположения наблюдателя и перебираемых с конечным шагом, зависящим от разрешения экрана. Благодаря этому объем вычислительных затрат в методе обратной трассировки существенно уменьшается по сравнению с методом прямой трассировки. Возможно комбинирование обоих методов для оптимизации алгоритмов и снижения их трудоемкости.

Алгоритмы трассировки носят характер рекурсивной процедуры, которая вызывает саму себя при появлении вторичного луча (анализируемый луч отражается или преломляется). Большая часть вычислений при реализации методов трассировки приходится на расчет пересечений лучей с поверхностями, в связи с чем они применяются для изображения оптических эффектов в сценах с небольшим числом объектов.

При практической реализации метода обратной трассировки вводят нижеприведенные ограничения. Некоторые из них необходимы, чтобы можно было в принципе решить задачу синтеза изображения, а некоторые ограничения позволяют значительно повысить быстродействие трассировки.

Ограничения метода обратной трассировки:

1. Среди всех типов объектов выделим источники света. Они могут только излучать свет, но не могут его отражать или преломлять. Обычно рассматриваются точечные источники.

2. Свойства отражающих поверхностей описываются суммой двух компонентов: диффузного и зеркального.

3. Зеркальность, в свою очередь, также описывается двумя составляющими. Первая (reflection) учитывает отражение от других объектов, не являющихся источниками света. Строится только один зеркально отраженный луч r для дальнейшей трассировки. Вторая компонента (specular) означает световые блики от источников света. Для этого направляются лучи на все источники определяются углы, образуемые этими лучами с зеркально отраженным лучом обратной трассировки (r). При зеркальном отражении цвет точки поверхности определяется цветом того, что отражается. В простейшем случае зеркало не имеет собственного цвета поверхности.

4. При диффузном отражении учитываются только лучи от источников света. Лучи от зеркально отражающих поверхностей игнорируются. Если луч, направленный на данный источник света, закрывается другим объектом, значит, данная точка объекта находится в тени. При диффузном отражении цвет освещенной точки поверхности определяется собственным цветом поверхности и цветом источников света.

5. Для прозрачных (transparent) объектов обычно не учитывается зависимость коэффициента преломления от длины волны. Иногда прозрачность вообще моделируют без преломления, т.е. направление преломленного луча t совпадает с направлением падающего луча.

6. Для учета освещенности объектов светом, рассеиваемым другими объектами, вводится фоновая составляющая (ambient).

7. Для завершения трассировки вводят некоторое пороговое значение освещенности, которое уже не должно вносить вклад в результирующий цвет, либо ограничивают число итераций.

Положительные черты метода обратной трассировки:

● универсальность, применимость для синтеза изображений достаточно сложных пространственных сцен. Воплощает многие законы оптики. Просто реализуются разнообразные проекции;

● даже усеченные варианты данного метода позволяют получить достаточно реалистичные изображения. Например, если ограничиться только первичными лучами (из точки проецирования), то это дает удаление невидимых точек. Трассировка уже одного-двух вторичных лучей дает тени, зеркальность, прозрачность;

● все преобразования координат (если таковые есть) линейны, поэтому достаточно просто работать с текстурами;

● для одного пиксела растрового изображения можно трассировать несколько близко расположенных лучей, а потом усреднять их цвет для устранения эффекта ступенчатости;

● поскольку расчет отдельной точки изображения выполняется независимо от других точек, то это может быть эффективно использовано при реализации данного метода в параллельных вычислительных системах, в которых лучи могут трассироваться одновременно.

Недостатки метода обратной трассировки:

● проблемы с моделированием диффузного отражения и преломления;

● для каждой точки изображения необходимо выполнять много вычислительных операций. Трассировка лучей относится к числу самых медленных алгоритмов синтеза изображений.