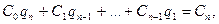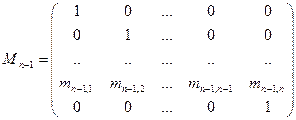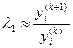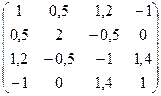Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Отыскание собственных значений матрицы
Академик А.Н.Крылов в 1931 году одним из первых предложил довольно удобный метод раскрытия определителя (2).
Суть метода А.Н.Крылова состоит в преобразовании определителя D() к виду
Равенство нулю определителя D() есть необходимое и достаточное условие для того, чтобы однородная система линейных алгебраических уравнений
имела решение х1, х2, …, хn, отличное от нулевого.
Преобразуем систему (2) следующим образом. Умножим первое уравнение на и заменим x1, …,xn их выражениями (2) через x1,…, xn.
Умножим далее уравнение (3) на и заменим снова x1, …,xn их выражениями через x1,…, xn. Получим
Повторяя этот процесс (n-1) раз, мы перейдем от системы (2) к системе
коэффициенты которой будут определятся по рекуррентным формулам
Очевидно, что определитель системы (5) будет иметь вид (1).
Система линейных алгебраических уравнений (5) имеет ненулевое решение для всех значений , удовлетворяющих уравнению D()=0. Таким образом, D1()=0 при всех , удовлетворяющих уравнению D()=0.
Пусть все корни D() различны. Так как все корни D() являются корнями D1(), то D1() делится на D(). Так как, кроме того, степени D1() и D() одинаковы, то частное должно быть постоянным. Сравнивая коэффициенты при n, получим
В случае, если D() имеет кратные корни, равенство (8) сохраняется.
Рассмотрим теперь коэффициенты bik, определяющие D1(). Введем в рассмотрение векторы Bi с компонентами bi1, bi2, …, bin. Равенства
показывают, что Bi=ABi-1, где A — матрица, транспонированная к данной. Из этого следует, что
Bi=A i-1B1, B1=AB0, (9)
Если С0, то уравнения D1()=0 и D()=0 эквивалентны. Если же С=0, то это преобразование ничего не дает. А.Н.Крылов предлагает в этом случае особый прием, рассмотренный ниже. Возьмем в качестве вектора В0 произвольный вектор В0=(bi1,bi2,…,bin) и получим с его помощью по формулам (9) векторы Вi.
Пусть u=b01x1+b02x2+…+b0nxn (10)
где x1,x2,…xn — решения системы (1/). Тогда повторяя прежние рассуждения, получим:
Решая эту систему как систему линейных однородных уравнений с n+1 неизвестными u,x1,x2,…xn, получим, что ненулевое решение возможно в том и только в том случае, когда
Повторяя прежние рассуждения, найдем, что
если С10, то коэффициенты рi характеристического многочлена определяются как отношения где Di — алгебраические дополнения элементов n-i в определителе D().
Но сущность метода Крылова и состоит в том, чтобы находить эти коэффициенты, не подсчитывая миноры.
Воспользуемся теоремой Гамильтона — Кэли о том, что матрица является корнем своего характеристического уравнения, т.е.
где рi — коэффициенты характеристического многочлена.
Умножая равенство (14) на b0, получим:
Это векторное равенство дает систему линейных алгебраических уравнений для определения коэффициентов характеристического многочлена. Определитель этой системы равен С1. Решать полученную систему можно любым из известных методов, например, методом Гаусса.
Можно было бы применить теорему Гамильтона — Кэли и для самой матрицы А, получили бы тогда систему
здесь ci=Aic0, c0
— произвольный начальный вектор.
Пример. Пусть матрица A имеет вид:
в качестве вектора В0 возьмем вектор В0=(1,0,0,0). Тогда получим векторы
В1=АВ0, В2=А2В0= АВ1, В3=А3В0=АВ2, В4=А4В0=АВ3:
Система линейных алгебраических уравнений для определения коэффициентов характеристического многочлена имеет вид:
Решив эту систему, получим: р1=-11, р2=7, р3=72, р4=-93. Поэтому характеристический многочлен примет вид:
D()= 4 -113 + 72 +72 -93.
В приведенном примере С10.
В случае, если С=0, такая система не даст возможности определить коэффициенты характеристического уравнения. Матрица А и транспонированная к ней матрица А удовлетворяет своему характеристическому уравнению D(A)=0. Но может оказаться, что существуют многочлены () степени меньше n, для которых также выполняется равенство (А)=(А)=0. Среди таких многочленов имеется единственный многочлен со старшим коэффициентом 1, имеющим наименьшую степень. Этот многочлен называется минимальным. Если минимальный многочлен матрицы не совпадает с характеристическим, то С=0 при любом выборе начального вектора. В этом случае АС0=0 и векторы С0, АС0, …,Аn-1C0 линейно зависимы.
На практике при использовании метода Крылова такая ситуация может возникнуть лишь при особых обстоятельствах.
Можно подсчитать, что при раскрытии характеристического многочлена матрицы с помощью метода Крылова потребуется 0,5(2п3+п2+п) операций умножения и деления.
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Задания лабораторной работы №3
Лабораторная работа №3
«Нахождение собственных чисел и собственных векторов матрицы»
1. Метод Крылова. Собственные числа матрицы А определяют путём решения характеристического уравнения, приведённого к виду
Значение 
где 


Собственные векторы матрицы А определяют из соотношения

где 

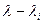
Пример решения задачи методом Крылова
A =
1. Для определения коэффициентов характеристического уравнения
строим последовательность векторов:
Если векторы В0, В1, В2, В3 окажутся линейно независимыми, то коэффициенты p1, p2, p3, p4 определяются из решения системы линейных уравнений, соответствующей равенству
Систему линейных уравнений решаем средствами Excel или MathCAD, можно воспользоваться также программной реализацией метода Гаусса из лабораторной работы №1.
| А | В0 | В1 | В2 | В3 | В4 | |
| 2,2 | 0,5 | 2,2 | 10,09 | 52,373 | 291,0006 | |
| 1,3 | 6,5 | 41,84 | 239,605 | |||
| 0,5 | 0,5 | 1,6 | 0,5 | 6,55 | 37,64 | 220,7825 |
| 1,6 | 10,20 | 57,56 | 321,930 |
Таким образом, характеристическое уравнение матрицы имеет вид

2. Определение собственных чисел матрицы состоит в решении полученного характеристического уравнения (*), например, средствами Excel или MathCAD, можно использовать программную реализацию одного из методов лабораторной работы №2.
Собственные числа матрицы А таковы:
3. Собственный вектор Xi, соответствующий собственному числу li , определяется по формуле
где коэффициенты при ранее найденных векторах В0, В1, В2, В3 находятся из равенства

Окончательные значения собственных векторов должны иметь кубическую норму, равную единице. Для того, чтобы собственный вектор имел кубическую норму, равную единице, нужно разделить все компоненты вектора на максимальную по модулю компоненту.
Все вычисления приведены в таблице 2.
| li | bi3B0 | bi2B1 | bi1B2 | bi0B3 | Xi |  |
| 5,652 | 0,4877 | –4,7672 –2,1669 –1,0334 –4,3338 | –3,5113 –2,2620 –2,2794 –3,5496 | 52,373 41,84 37,64 57,56 | 44,5822 37,4111 34,2772 49,6766 | 0,879 0,753 0,690 1,0 |
| 1,545 | 1,7918 | –15,5826 –7,08298 –3,5415 –14,1660 | –44,9510 –28,9575 –29,1802 –45,4410 | 52,373 41,84 37,64 57,56 | –6,3688 5,7995 4,9183 –2,0470 | –0,911 –0,772 0,321 |
| –1,420 | –1,9427 | 22,7400 10,3364 5,1682 20,6728 | –74,8678 –48,2300 –48,6010 –75,6840 | 52,373 41,84 37,64 57,56 | –1,6975 3,9464 –5,7928 2,5488 | 0,293 –0,681 –0,440 |
| 0,2226 | 12,4042 | –5,2692 –1,4860 –0,7430 –2,9720 | –58,2940 –37,5531 –37,8420 –58,9295 | 52,373 41,84 37,64 57,56 | 3,2140 2,8009 –0,9450 –4,3415 | –0,740 –0,645 –0,218 |
2. Метод Данилевского. Для определения коэффициентов характеристического уравнения матрицу A с помощью n-1 преобразований подобия заменяют подобной ей матрицей Фробениуса
P=
На первом этапе находят:
где
где

где
Пример решения задачи методом Данилевского
A =
1. Коэффициенты характеристического уравнения матрицы А определяются как элементы первой строки матрицы Фробениуса Р, подобной данной матрице А. Матрицу Р найдем в результате трех преобразований подобия:
Округляя значения коэффициентов до четырех десятичных знаков, получим характеристическое уравнение
l 4 – 6l 3 – 0,2l 2 + 12,735l – 2,7616 = 0.
Это уравнение решаем средствами Excel или MathCAD, можно использовать программную реализацию одного из методов лабораторной работы №2. Корни уравнения таковы:
2. Собственный вектор Xi , соответствующий собственному числу li , определяется равенством
Xi = М3 ×М2× М1×Yi, где Yi = 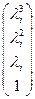
Результаты вычисления собственных векторов приведены в таблице 3.
| li | M1 | M2 | M3 | Yi | Xi |  |
| 5,652 | –0,231125 1,078582 1,651001 1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 180,5537 31,9451 5,652 | 0,8977 0,7529 0,6898 | 0,898 0,753 0,690 |
| 1,545 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 3,6880 2,3870 1,545 | 3,1143 –2,8359 –2,4048 | –0,911 –0,772 –0,440 |
| 0,2226 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 0,01103 0,4955 0,2226 | –0,7403 –0,6451 0,2177 | –0,740 –0,645 0,218 |
| –1,420 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | –2,8633 2,0164 –1,420 | –0,6665 1,5480 –2,2719 | 0,293 –0,681 –0,440 |
3. Метод итераций для определения первого собственного значения и соответствующего ему собственного вектора матрицы А. Строят последовательность векторов: 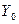

где 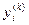

При этом собственный вектор 
Пример решения задачи методом итераций
1. Строим последовательность векторов 


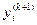

Все вычисления приведены в таблице 4.
Таблица 4
| 1,6 | 2,3 | 1,2 | ||||
| A | 2,3 | 0,6 | 1,5 |  |  |  |
| 1,2 | 1,5 | 3,8 | ||||
 | ||||||
 | 5,1 | 4,4 | 6,5 | 5,11 | 5,48 | 5,76 |
 | 26,08 | 24,12 | 37,42 | 5,45 | 5,41 | 5,60 |
 | 142,108 | 130,586 | 209,672 | 5,484 | 5,511 | 5,548 |
 |  |  |  | 5,5151 | 5,5148 | 5,5321 |
 |  |  |  | 5,5205 | 5,5225 | 5,5267 |
 |  |  | 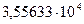 | 5,5233 | 5,5235 | 5,5251 |
 |  |  |  | 5,5240 | 5,5241 | 5,5246 |
 | 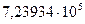 |  |  | 5,5242 | 5,5243 | 5,5244 |
 | 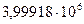 |  |  | 5,5243 | 5,5243 | 5,5244 |
 |  |  |  | 5,5243 | 5,5243 | 5,5243 |
 |  |  |  |
Итак, 
2. Собственный вектор 





Задания лабораторной работы №3
«Нахождение собственных чисел и собственных векторов матрицы»
Задание для нечетных вариантов:
1. Используя метод Крылова найти собственные числа и собственные вектора матрицы А. Разрешается реализовывать метод Крылова средствами MathCAD или Mathematica (корни характеристического уравнения найти с помощью встроенных функций). Метод Крылова можно реализовать также на VBA (корни характеристического уравнения найти с помощью команды «Поиск решения» или «Подбор параметра» пункта меню Сервис в Excel).
2. Используя метод итераций, определить первое собственное число матрицы (наибольшее по модулю). Найти соответствующий ему собственный вектор, имеющий кубическую норму, равную 1. Метод итераций реализовать на языке программирования.
3. Сравнить результаты, полученные методом Крылова и методом итераций.
Задание для четных вариантов:
1. Используя метод Данилевского найти собственные числа и собственные вектора матрицы А. Разрешается реализовывать метод Данилевского средствами MathCAD или Mathematica (корни характеристического уравнения найти с помощью встроенных функций). Метод Данилевского можно реализовать также на VBA (корни характеристического уравнения найти с помощью команды «Поиск решения» или «Подбор параметра» пункта меню Сервис в Excel).
2. Используя метод итераций, определить первое собственное число матрицы (наибольшее по модулю). Найти соответствующий ему собственный вектор, имеющий кубическую норму, равную 1. Метод итераций реализовать на языке программирования.
3. Сравнить результаты, полученные методом Данилевского и методом итераций.
Варианты заданий
№1. A = 
№3. A = 
№5. A = 
№7. A = 
№9. A = 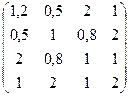
№11. A = 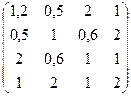
№13. A = 
№15. A = 
№17. A = 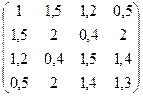
№19. A = 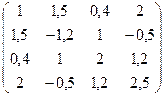
№21. A = 
№23. A = 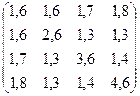
№25. A = 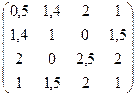
№27. A = 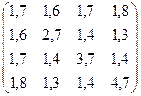
№29. A = 
Видео:Собственные векторы и собственные значения матрицыСкачать

Решение системы уравнений методом крылова
Найти собственные значения и собственные вектора матрицы методом Крылова:
Основан на том, что матрица обращает в 0 свой характеристический многочлен, т.е. матрица является корнем своего характеристического уравнения.
Берется нулевой вектор y(0) ина него умножается полученное уравнение.
В результате получаем:
Найдем значения p



Выберем в качестве y(0)=
Найдем p(i),затем из p(i)=>l(i) ,решив характеристическое уравнение.
Где q(j, i)-формируется по схеме Горнера
Double func1(double y, int mode);
Double metod_neutona(double a, double b, double (*function)(double, int));
Int find_interval_izol(double *a, double *b, double (*function)(double, int));
Double AA[4][4];//то же что и А
Double M[4][4];//некая неособенная матрица
Double M_1[4][4];//обратная неособенной
Double C[4][4];//хранит рез-т перемножения матриц
Double P[4];//коэф-ты хар-кого ур-я
Double L[4];//собственные значения матрицы
Double Q[4][4];//матрица значений q
Double Y[4][5];//матрица значений Y
Double X[4][4];//матрица собственных векторов матрицы A
Double x0,h, E=0.000001;
int i, j,k, number_vector=0;
printf(» Исходная матрица А»);
for(j=0;j 0) x0=a; //выбор точки x0
else if(function(b,0)*function(b,2)>0) x0=b; //
Int find_interval_izol(double *a, double *b, double (*function)(double, int))
📺 Видео
А.7.35 Собственные вектора и собственные значения матрицыСкачать

Собственные значения и собственные векторы. ТемаСкачать

Собственные векторы и собственные числа линейного оператораСкачать

Собственные значения и собственные векторы. ПримерСкачать

Собственные значения и собственные векторыСкачать

Все на выброс или с чего начинать ремонт объектаСкачать

Решение матричных уравненийСкачать

Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

7 4 Собственные векторы и собственные значенияСкачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Как разложить вектор по базису - bezbotvyСкачать

лекция проф. Ефимова В.А., СПбГУТ 5.10.11Скачать

Вычислительные методы алгебры - Степенной метод, метод вращенийСкачать

Собственные значения матрицыСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Практика 1. Часть 1. Собственные вектора и значения линейного оператора. Канонический вид.Скачать