Предположим, что у вас есть произвольный треугольник с вершинами A , B и C . В этой статье (раздел 4.2) говорится, что вы произвольно генерируете случайную точку P равномерно из треугольника ABC следующей выпуклой комбинация вершин:
где r1 и r2 равномерно вычерчены из [0, 1] , а sqrt — функция квадратного корня.
Как вы подтверждаете, что выбранные точки, равномерно распределенные в треугольнике ABC ?
ИЗМЕНИТЬ
Видео:Алгоритмы. Попадание точки в треугольникСкачать

ОТВЕТЫ
Ответ 1
У вас есть карта P (r1, r2) от квадрата единицы к вашему треугольнику. Выбор r1 и r2 равномерно дает случайную точку в единичном квадрате. Изображение в треугольнике распределяется по определителю Якобиана отображения P, которое оказывается константой. Поэтому распределение изображения равномерно.
Собственно, для проверки этого вам нужно только проверить его на одну тройку неколлинеарных точек A, B, C. Аффинные линейные отображения имеют постоянный якобиан, поэтому вы можете применить один из них, чтобы переместить произвольную тройку в эту стандартную позицию, не влияя на распределение.
Наконец, слово о «почему»: Рассмотрим треугольник как заполненный отрезками, параллельными стороне BC. В формуле для P переменная r1 выбирает, на какой сегмент будет стоять точка, тогда как r2 определяет, где по сегменту она будет. Для однородности все точки на данном сегменте должны обрабатываться одинаково (следовательно, линейными по r2). Но для r1, так как некоторые сегменты короче других, нам нужно отдавать предпочтение длинным сегментам для достижения равномерного распределения. Для этого отвечает sqrt (r1) в формуле.
Видео:Игры хаоса. Фракталы [Numberphile на русском]Скачать
![Игры хаоса. Фракталы [Numberphile на русском]](https://i.ytimg.com/vi/Nx3_nX8UoMo/0.jpg)
Равномерное распределение точек в треугольнике
Большинство двухмерных квазислучайных методов рассчитано на сэмплирование в единичном квадрате. Однако в компьютерной графике также очень важны треугольники. Поэтому я описал простой метод прямого построения для равномерного покрытия последовательностью точек треугольника произвольной формы.
Рисунок 1. Новый прямой метод построения открытой (бесконечной) квазислучайной последовательности с низким расхождением в треугольнике произвольной формы и размера. На рисунке показаны распределения точек в пятнадцати случайных треугольниках для первых 150 точек.
Видео:Где находится точка в треугольнике заданном координатами вершин, внутри или вне треугольника.Скачать

Краткий обзор
Последовательности с низким расхождением (low discrepancy), равномерно сэмплирующие/заполняющие квадрат, активно изучались почти сотню лет. БОльшую часть этих квазислучайных последовательностей можно расширить до прямоугольников простым растягиванием, не сильно повредив при этом расхождению.
Однако в этом посте мы рассмотрим интересное и важное расширение последовательностей с низким расхождением на произвольный треугольник.
Насколько я мог понять, построению множеств равномерно распределённых в треугольнике точек и последовательностей уделялось очень мало внимания. Примечательные работы недавних лет Басу [2014], Пилландса [2005] и Брандолини [2013] представляют основные, если не единственные статьи по этой теме.
Эти авторы обычно рассматривают эту проблему под очень теоретическим и аналитическим углом, и почти всегда решают её для единичного правильного треугольника. В отличие от них, мой пост в основном предназначен для разработки практических техник в рендеринге графики.
В посте описывается простой метод прямого построения, не требующий ни принятия/исключения, ни отбрасывания или рекурсии; и самое важное то, что его можно применять к треугольникам произвольного размера и формы.
Пост состоит из четырёх разделов:
- Квазислучайные последовательности в квадрате
- Наложение единичного квадрата на треугольник.
- Снижение искажений
- Дальнейшие обобщения
Видео:Точка пересечения медиан в треугольникеСкачать

1. Квазислучайные последовательности точек
Вы можете подумать, что разместить 100 точек в квадрате таким образом, чтобы минимальное расстояние между соседними точками оставалось как можно бОльшим, будет легко. Но что если нужно разместить 13 точек? 47? А как насчёт 2019 точек?!
Оказывается, что последовательности точек с низким расхождением обеспечивают систематический способ решения этой задачи. Существует множество квазислучайных последовательностей с низким расхождением, от простой последовательности Холтона до более сложной последовательности Соболя. Каждая из этих последовательностей имеет свои достоинства и недостатки. Например, последовательности Холтона оказываются более полезными при размещении объектов в области, потому что у неё хорошо оптимизированы такие метрики локального расстояния, как ближайшие соседи. Последовательность Соболя склонна к образованию большей «скученности», однако глобальное распределение точек очень равномерно, поэтому она имеет превосходные свойства квадратуры.
Есть ещё одна последовательность, которую я люблю использовать, с отличными локальными, а также глобальными свойствами. Это последовательность , подробно описанная в моём предыдущем посте «Неожиданная эффективность квазислучайных последовательностей».
Если вкратце, то мы задаём бесконечную двумерную последовательность , такую, что
Подробнее об этом особом значении , которое часто называют «пластической константой» можно прочитать в Википедии или Mathworld.
В итоге, на рисунке 2 показано сравнение различных последовательностей с низким расхождением (и простая равномерная случайная выборка для сравнения). Как видите, эта случайная выборка демонстрирует скапливание точек. При этом в ней есть области, вообще не содержащие точек («белый шум»), в то время как квазислучайная последовательность с низким расхождением — это метод построения (бесконечной) последовательности точек детерминированным образом так, чтобы на любом этапе размещённые точки равномерно распределялись по всему пространству.
Рисунок 2. Иллюстрация первых 150 членов различных квазислучайных последовательностей с низким расхождением. Заметьте, что все они создают более равномерно распределённые в пространстве точки, чем простое равномерное случайное распределение (внизу слева).
Видео:Замечательные точки треуг-ка. 8 класс.Скачать

2. Наложение единичного квадрата на треугольник
Существует три хорошо известных способа, позволяющих обеспечить равномерную случайную выборку из треугольника:
Рисунок 3. Метод параллелограмма
Метод параллелограмма заключается в следующем.
Для треугольника рассмотрим параллелограмм
.
Для точки единичного квадрата зададим такую точку
, что
.
Эта точка всегда будет находиться внутри параллелограмма. Однако если она оказывается в дополнительном треугольнике , то нам нужно отразить её обратно в треугольник
.
То есть если , то
, но если
1$» data-tex=»inline»/>, то
.
Однако очень важно понимать, что даже хотя эти методы обеспечивают равномерную выборку из треугольника, это не означает, что такое преобразование сохранит равномерное пространственное расположение (т.е. низкое расхождение) наших квазислучайных распределений точек.
Например, в случае метода параллелограмма отражение может часто приводить к тому, что точка окажется очень близко к другой существующей точке. Очевидно, что это разрушает структуру с низким расхождением и проявится как искажения/полосы.
Аналогично, метод инверсного распределения накопленных вероятностей применяет к точкам нелинейное искажение. В последовательностях Холтона и Соболя это означает, что две точки очень часто подталкиваются очень близко друг к другу.
На рисунке 4 показано, насколько хорошо сохраняется низкое расхождение в каждой из различных квазислучайных последовательностей при преобразовании области из единичного квадрата в треугольник при использовании метода параллелограмма.
Рисунок 4. Сравнение преобразования различных квазислучайных последовательностей в треугольнике. Вверху показана последовательность Холтона, посередине — последовательность Соболя, внизу — последовательность . Видно, что в последовательности Холтона возникает значительная скученность точек, а в последовательности Соболя — значительное образование полос. По сравнению с ними, в последовательности
точки распределены очень равномерно, и почти отсутствует заметная скученность или полосы.
Из трёх различных методов триангуляции и множества различных квазислучайных последовательностей метод параллелограмма, применённый к методу последовательности , является единственной комбинацией, постоянно создающей результаты, приемлемые с точки зрения сохранения низкого расхождения без искажений.
Превосходные результаты этого сочетания можно подробнее рассмотреть на рисунке 5.
Рисунок 5. Можно увидеть, что преобразованная последовательность обеспечивает очень простой, но эффективный способ равномерного распределения множества из
точек в треугольнике. Он работает и с остроугольными, и с тупоугольными треугольниками. (Цвет обозначает порядок расположения).
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

3. Другие аспекты
Видео:№238. Докажите, что в равнобедренном треугольнике отрезок, соединяющий любую точку основания,Скачать

Искажение
Метод параллелограмма требует выбора двух сторон треугольника в качестве базисных векторов.
Если вершины помечаются в случайном порядке, то паттерны точек обычно напоминают показанные на рисунке 6.
Рисунок 6. Паттерны точек, получающиеся при случайном выборе порядка вершин. Заметьте, что в большинстве случаев явно заметно искажение.
Однако оказывается, что при продуманном выборе порядка вершин можно значительно снизить искажения. Наиболее примечательно то, что если треугольник пометить так, что является наибольшим углом (то есть против него лежит наибольшая сторона), то стороны
и
используются в качестве двух сторон параллелограмма.
Если принять такой порядок, то получаются паттерны точек, показанные выше на рисунках 1, 4 и 5.
Однако даже при определённом порядке вершин в некоторых случаях всё равно заметны эффекты искажений. Больше всего они заметны, когда в треугольниках один из углов очень мал. В случае тупоугольных треугольников, когда наименьший угол меньше 30 градусов, то заметно некоторое искажение, а в случае остроугольных треугольников, когда наименьший угол меньше 20 градусов, становится видным искажение. (Если сэмплируемые треугольники являются частью сетки Делоне, то такие проблемы с искажениями могут быть минимальными, потому что триангуляция Делоне специально предназначена для минимизации количества треугольников с малыми углами.)
Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Другие фигуры
К сожалению, технику параллелограмма невозможно использовать для других фигур, потому что в нём используется симметрия треугольника. Для некоторых фигур можно получить хорошие результаты с помощью метода инверсного распределения накопленных вероятностей. Ниже показан пример того, как последовательность с низким расхождением можно преобразовать в область, ограниченную гауссовой кривой с сохранением равномерного расстояния между точками.
Видео:№54. Точка В не лежит в плоскости треугольника ADC, точки М, N и Р — середины отрезков ВА, ВССкачать
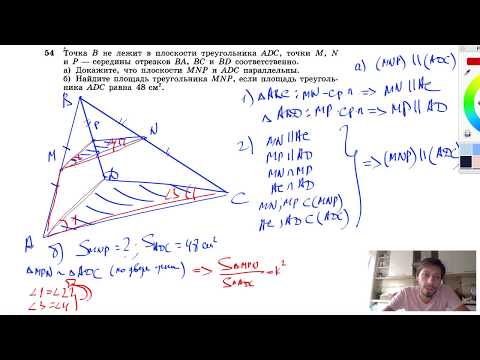
Геометрическая вероятность
Цели и задачи: 1) Познакомить учащихся с одним из возможных способов задания
2) Повторение пройденного и закрепление навыков формализации
текстовых вероятностных задач с помощью геометрических фигур.
1) Знать определение геометрической вероятности выбора точки
внутри фигуры на плоскости и прямой;
2) Уметь решать простейшие задачи на геометрическую вероятность,
зная площади фигур или умея их вычислять.
I. Выбор точки из фигуры на плоскости.
Пример 1. Рассмотрим мысленный эксперимент: точку наудачу бросают на квадрат, сторона которого равна 1. Спрашивается, какова вероятность события, которое состоит в том, что расстояние от этой точки до ближайшей стороны квадрата не больше чем 

Рассмотрим более общие условия опыта.
Точку наудачу бросают в фигуру F на плоскости. Какова вероятность того, что точка попадает в некоторую фигуру G, которая содержится в фигуре F.
Ответ зависит от того, какой смысл мы вкладываем в выражение «бросить точку наудачу».
Обычно это выражение трактуют так:
1. Брошенная точка может попасть в любую часть фигуры F.
2. Вероятность того, что точка попадает в некоторую фигуру G внутри фигуры F, прямо пропорциональна площади фигуры G.
Подведем итог: пусть 


Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому


Точка удалена от границы квадрата не более чем на 


Тогда вероятность того, что точка попала в фигуру G, равна
Пример 2. Из треугольника АВС случайным образом выбирается точка Х. Найти вероятность того, что она принадлежит треугольнику, вершинами которого являются середины сторон треугольника.

Вероятность того, что точка Х принадлежит треугольнику KMN, равна:
Вывод. Вероятность попадания точки в некоторую фигуру прямо пропорциональна площади этой фигуры.
Задача. Нетерпеливые дуэлянты.
Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами утра и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти 5 минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком?
Решение: Пусть х и у обозначают время прибытия 1-го т 2-го дуэлянтов соответственно, измеренное в долях часа начиная с 5 часов.


📹 Видео
Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать

Всё о равнобедренном треугольнике за 1 минуту.Мой тг:matematikandreiСкачать

Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

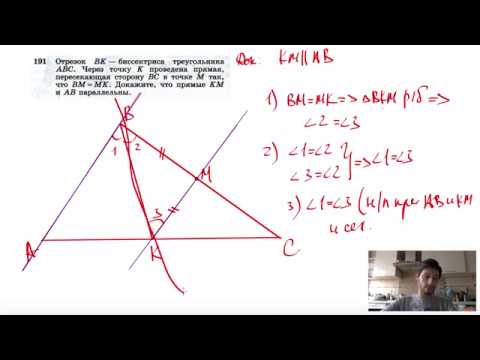
№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать
Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

0906 Замечательные линии и точки в треугольникеСкачать









