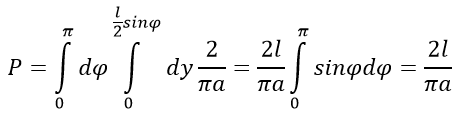Плоскость разграфлена параллельными прямыми находящимися на расстоянии 2а (3 видео)

Решение задачи Бюффона

Метод Бюффона основан на методе Монте-Карло и заключается в бросании иглы на плоскость, расчерченную на расстоянии друг от друга параллельными прямыми. Этот метод также применяется для вычисления числа π. Чем больше количества повторений опыта, тем точнее будет результат.

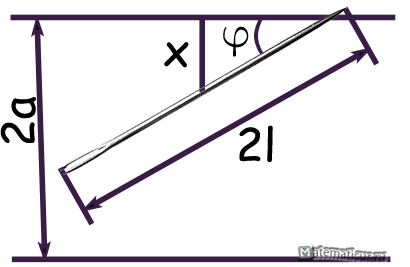
Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросают иглу длины 2l (2l≤2а), φ – угол. Найти вероятность того, что игла пересечет какую-нибудь прямую.

Решение

Графически задачу Бюффона можно представить следующем образом: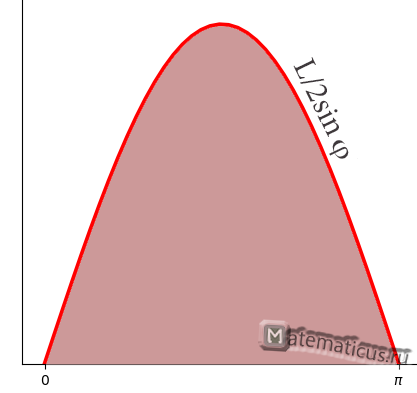

Найдем вероятность через вычисления интеграла:

Экспериментально по методу Монте-Карло вероятность определяется по формуле:

P≈[кол-во бросаний]/[кол-во пересечений]

Число π приближенно можно определить по методу Монте-Карло по формуле:

π≈2L*[кол-во бросаний]/ a *[кол-во пересечений]

a — расстояние между линиями.

Если мы сделаем предположение, что длина иглы равна расстоянию между линиями, то выражение определяется по формуле:

π≈ 2 *[кол-во бросаний] / [кол-во пересечений]

В практических вычислений вероятности также используют условие, что параллельные линии находятся друг от друга на расстояние двух длин иглы

Содержание

Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2A. На плоскость наудачу
Ваш ответ
решение вопроса
Похожие вопросы
Теория вероятности (много задач)
🎬 Видео

Видео:Расстояние между параллельными прямымиСкачать

Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2A. На плоскость наудачу

Видео:Параллельность прямой к плоскостиСкачать

Ваш ответ

Видео:Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

решение вопроса

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Теория вероятности (много задач)

Брошены две игральные кости. Найти вероятность того, чтосумма очков на выпавших гранях – четная, причем на гранях хотя бы одной из костей появится шестерка.

На выпавшей грани «первой» игральной кости может появиться одно очко, два очка,…, шесть очков. Аналогичные шесть элементарных исходов возможны и при бросании другой кости. Каждый из исходов бросания «первой» может сочетаться с каждым из исходов бросания «второй». Таким образом общее число возможных элементарных исходов испытания равно . Эти исходы образуют полную группу и в силу симметрии костей равновозможны.

Благоприятствующими интересующему нас событию (хотябы на одной грани появится шестерка, сумма выпавших очков четная) являются следующие пять исходов

1)6, 2 2)6, 4 3)6, 6 4)2, 6 5)4, 6

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов испытания:

При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятиссть того, что была утеряна:

А) стандартная деталь; б) нестандартная деталь.

а) Извлеченная стандартная деталь, очевидно, не могла быть утеряна; могла быть потеряна любая из остальных 30 деталей (21+10—1=30), причем среди них было 20 стандартных (21-1=20). Вероятность того, что была потеряна стандартная деталь, Р= 20/30 = 2/3.

Б) Среди 30 деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь,

Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число; б) случайно названное двузначное число, цифры которого различны.

А) Мы рассматриваем событие:

А – задуманным двузначным числом оказалось случайно названное двузначное число.

Для этого события общее число возможных элементарных исходов n = 90, т. е. количество всех двузначных чисел. А число возможных исходов, благоприятствующих событию m = 1, т. е. только одно двузначное число будет равно задуманному.

Итак, по классическому определению вероятности получаем:

Б) Мы рассматриваем событие:

А – задуманным двузначным числом оказалось случайно названное двузначное число, цифры которого различны.

Для этого события общее число возможных элементарных исходов n = 81, т. е. количество всех двузначных чисел, цифры которого различны. А число возможных исходов, благоприятствующих событию m = 1, т. е. только одно двузначное число будет равно задуманному.

Итак, по классическому определению вероятности получаем:

Ответ: а)1/90 ; б)1/81

Задание: Указать ошибку «решения» задачи: брошены две игральные кости, найти вероятность того, что сумма очков на костях будет равна 3 (событие ).

Возможны два исхода события: сумма выпавших очков равна 3, сумма выпавших очков не равна 3. Событию благоприятствует один исход; общее число исходов равно двум. Следовательно, искомая вероятность

. Ошибка этого решения состоит в том, что рассматриваемые исходы не являются равновозможными.

Правильное решение: Общее число равновозможных исходов испытания равно (каждое число очков, выпавших на одной кости, может сочетаться со всеми числами очков, выпавших на другой). Среди этих исходов событию может благоприятствовать только два исхода: Следовательно, искомая вероятность .

Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) Сумма выпавших очков равна восьми, а разность – четырём; в) Сумма выпавших очков равна восьми, если известно что их разность равна четырём; г) сумма выпавших очков равна пяти, а произведение — четырём.

Общее число равно равновозможных исходов равно 6*6=36 (Каждое число на одной кости может сочетаться со всеми числами очков, выпавших на другой кости)

А) среди общего количества исходов событию А благоприятствуют только 6 : (1.6), (6,1),(2,5),(5,2),(3,4),(4,3) следовательно искомая вероятность 6/36=1/6

Б) среди общего количества исходов событию А благоприятствуют только 6 : (2.6), (6,2),(3,5),(5,3),(4,4),(4,4), но в следствии того что разность равна 4 останется только два события: (2,6) и (6,2). Следовательно искомая вероятность 2/36=1/18

В) Общее число исходов события А равно 4: (6,2) (2,6) (5,1) (1,5) (т. к. разность должна быть равна 4). Среди общего количества исходов события А благоприятствуют только 2: (6,2) и (2,6). Следовательно искомая вероятность равна 2/4 = ½

Г) среди общего количества исходов событию А благоприятствуют только 4 : (1,4), (4,1),(3,2),(2,3), но в следствии того что произведение равно 4 останется только два события: (1,4) и (4,1). Следовательно искомая вероятность 2/36=1/18

Общее число равновозможных исходов равно 1000 (всего столько кубиков). Среди этих исходов благоприятствуют событию только 384 исхода (64 маленьких кубика имеют одну окрашенную грань на грани большого, граней у куба 6, поэтому ) следовательно искомая вероятность . Благоприятствует событию только исходов, т. е. . А событию – 8 исходов (только на углах большого куба у маленьких кубиков окрашены 3 грани), т. е. .

Монета брошена 2 раза. Найти вероятность того, что хотя бы один раз появится «герб».

Решение: Всего различных случаев выпадения монеты – 4. Обозначим как 1- выпала «решка», 0 – выпал «герб». Тогда можем составить таблицу:

Т. е. всего удовлетворяющих нас выпадений – 3 из 4. Следовательно, вероятность того, что выпадет хоть один «герб» равна PA= mn= 34;

Число всевозможных исходов эксперимента – 720

(Так как нам важно, в каком порядке извлекаются кубики, то для подсчёта всех возможных исходов необходимо найти все их перестановки, то есть n==6!=720)

Число исходов, удовлетворяющих поставленному условию – 1

Значит шанс, что все кубики извлекутся в нужном порядке — 1/720

Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные 6).

Общее число элементарных исходов испытания равно числу сочетаний из 6 элементов по 3 с повторениями ().

Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равных 6) на гранях двух других костей, равно числу сочетаний без повторений из 5 элементов по 2 ().

Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов:

В пачке 20 перфокарт, помеченных номерами 101, 102, . , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.

Решение: Общее число элементарных исходов испытания равно числу сочетаний из 20 элементов по 2 с повторениями ().

Число исходов, благоприятствующих появлению перфокарт с номерами 101 и 120, равно числу сочетаний без повторений из 2 элементов по 2 () = 1.

В ящике 10 одинаковых деталей, помеченных 1,2,…,10. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажутся:

Б) деталь № 1 и № 2.

А) Общее число возможных элементарных исходов равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. .

Найдем число исходов, благоприятствующих интересующему нас событию: среди отобранных 6 деталей есть деталь № 1 и, следовательно, остальные пять деталей имеют другие номера. Число таких исходов, очевидно, равно числу способов, которыми можно отобрать 5 деталей из оставшихся 9, т. е. .

Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: P==0,6 .

Б) Число исходов, благоприятствующих интересующему нас событию (среди отобранных деталей есть детали № 1 и № 2, следовательно, четыре детали имеют другие номера), равно числу способов, которыми можно извлечь четыре детали из оставшихся восьми, т. е. C48.

Искомая вероятность P==1/3 .

В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 3 детали из 15 . Число исходов, благоприятствующих равно числу возможных вариантов извлечения 3 деталей из 10.

Искомая вероятность равна отношению С из 15 по 3 деленное на С из 10 по 3 .

В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 10 карточек из 100. = .

Число исходов, благоприятствующих равно числу возможных вариантов извлечения 9 карточек. 10ая карточка – это карточка интересующая нас. Это число равно .

Искомая вероятность равна отношению P=/ = 0,1 .

В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.

А) Общее число возможных элементарных исходов испытания равно количеству способов извлечь 4 детали из100, т. е. , число благоприятствующих рассматриваемому событию исходов равно количеству способов извлечь 4 не бракованные детали, т. е. . Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов:

Б) Число благоприятствующих рассматриваемому событию исходов равно количеству способов извлечь 4 бракованные детали, т. е. .

Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся два неизношенных элемента

Общее число возможных элементарных исходов испытания равно числу вариантов включения двух элементов из пяти, что составляет

Найдем число исходов, благоприятствующих интересующему нас событию: оба включенных элемента неизношенны, следовательно, все оставшиеся изношены. Чисто таких исходов равно числу способов, которыми можно извлечь два неизношенных элемента из трех:

Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов:

В партии из N деталей имеется п стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь m деталей из N деталей, т. е. —числу сочетаний из N элементов по m.

Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди m деталей ровно k стандартных): k стандартных деталей можно взять из п стандартных, деталей способами;

Число благоприятствующих исходов равно

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных окажутся три женщины.

Общее число равновозможных элементарных исходов испытания равно числу способов отбирания по табельным номерам Человек из , т. е числу сочетаний .

Найдем число исходов, благоприятствующих интересующему нас событию: трех из четырех можно отобрать способами. Остальные четыре человека будут мужчинами. Выбор четырех из шести мужчин можно осуществить способами. Следовательно число благоприятствующих исходов равно .

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех равновозможных элементарных исходов, т. е:

Ответ:

В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие.

А) Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь две детали из пяти, и равно числу сочетаний из пяти по два.

Одно окрашенное изделие можно взять из трех окрашенных изделий С31 способами.

А число способов взять одно неокрашенное изделие из двух неокрашенных равно С21 .

Число благоприятствующих условий равно С31 С21 .

Р= С31 *С21 /С52=0,6

Б) Р= С32 *С20 /С52=0,3

В) Р= С31 *С21 /С52 +С32 *С20 /С52=0,9

По цели произведено 20 выстрелов, причем зарегистрировано 18 попаданий. Найти относительную частоту попаданий в цель.

Относительная частота события А (попадание в цель) равна отношению числа попаданий к числу произведенных выстрелов:

На отрезке L длины 20 см помещён меньший отрезок L длины 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадает так же и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка, и не зависит от его расположения.

Т. к. вероятность попадания точки на отрезок пропорциональна длине отрезка, и не зависит от его расположения, то искомую вероятность можно найти по формуле

Подставляя наши значения (L=20; L=10) в данную формулу получаем искомую вероятность

На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка, и не зависит от его расположения на числовой оси.

Разобьём отрезок ОА на 3 отрезка длины L/3. Тогда для того чтобы меньший из отрезков ОВ и ВА имеет длину, большую чем L/3, необходимо чтобы наудачу поставленная точка B(x) попала в отрезок B, длина которого L=L/3. А т. к. вероятность

Попадания точки на отрезок пропорциональна длине отрезка, и не зависит от его расположения на числовой оси, то искомую вероятность можно найти по формуле

Подставляя наши значения (L=L; L=L/3) в данную формулу получаем искомую вероятность

В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка наудачу брошенная в большой круг попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга, и не зависит от его расположения.

Т. к. вероятность попадания точки в круг пропорциональна площади круга, и не зависит от его расположения, то мы можем вычислить вероятность того, что точка наудачу брошенная в большой круг попадет также и в малый круг по формуле:

(*)

Где G—Площадь малого круга, а G—Площадь большого круга. Вычислим площади.

Подставив их в формулу (*) получим искомую вероятность

Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2A. На плоскость наудачу брошена монета радиуса R =C

Аналогичное утверждение. Должны одновременно выполняться 2 условия: y x/2.

Как видно из рисунка, все эти точки принадлежат заштрихованному треугольнику ORK.

Таким образом, фигуру ONRK можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию.

На отрезке ОА длины L числовой оси Ох наудачу поставлены две точки В(х) и С(у), причём . Найти вероятность того, что длина отрезка ВС окажется меньше, чем L/2. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

Координаты точек В и С должны удовлетворять неравенствам

Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей прямоугольному треугольнику OL1 K. Таким образом, этот треугольник можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек В и С.

Длина отрезка BC должна оказаться меньше L/2, т. е имеет место неравенство:

Y =C. Имеет место неравенство .

Эти условия выполняются для фигуры OFSRNP( см. рисунок).Таким образом, эту фигуру можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию.

Задача Бюффона (французский естествоиспытатель XVIII в.). плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2a. На плоскость наудачу бросают иглу длины 2L (L х и x — y y, или, что то же,

У>х—t при у х и x — y y, или, что то же,

У>х—t при у z; x+z>y;
y+z>x> — куб со стороной длины L без трех тетраэдров

Наудачу взяты два положительных числа х и у, каждое из которых не превышает двух. Найти вероятность того, что произведение ху будет не больше единицы, а частное у/x не больше двух.

Числа удовлетворяют неравенствам . Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OLRM. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек х и у. Согласно условию задачи, имеют место следующие неравенства:

(см. рисунок).

Заштрихованную область можно принять за фигуру g, координаты точек которой благоприятствуют интересующему нас событию.

Нетрудно видеть, что

Наудачу взяты два положительных числа х и у, каждое из которых не превышает единицы. Найти вероятность того, что сумма х+у не превышает единицы, а произведение ху не меньше 0,09.

Числа х и у должны удовлетворять неравенствам: . Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OLRM. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек х и у.

Согласно условию задачи, имеют место следующие неравенства: (си. Рисунок). Заштрихованную область можно принять за фигуру g, координаты точек которой благоприятствуют интересующему нас событию.

Нетрудно видеть, что

На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Обозначим искомое событие А, а противоположное ему В(ни один из взятых учебников не окажется в переплете). Так как сумма вероятностей двух противоположных событий равно 1, то

Р(А)=1- С103 /С153=1-24/91=67/91

В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена (событие А).

Требование – хотя бы одна из взятых деталей окрашена – будет осуществлено, если произойдет любое из следующих трех несовместных событий: B – одна деталь окрашена, C – две детали окрашены, D – три детали окрашены.

Интересующее нас событие A можно представить в виде суммы событий: A=B+C+D. По теореме сложения,

Найдем вероятность событий B, C и D:

Доказать, что если событие А влечёт за собой событие В, то Р(В) ≥ Р(А)

Событие В можно представить в виде суммы несовместных событий и : = + .

По теореме сложения вероятностей несовместных событий получим

Так как , то

Вероятности появления каждого из двух независимых событий А1 и А2 соответственно равны р1 и p2. Найти вероятность появления только одного из этих событий.

Введем обозначения событий: В1 – появилось только одно событие А1, В2 – появилось только событие А2.

Появление события В1 равносильно появлению события (появилось первое событие и не появилось второе), т. е. В1 = . Появление события В2 равносильно появлению события (появилось второе событие и не появилось первое), т. е. В2 = .

Таким образом, чтобы найти вероятность появления только одного из событий А1 и А2, достаточно найти вероятность появления одного, безразлично какого, из событий В1 и В2. События В1 и В2 несовместны, поэтому применима теорема сложения:

Остается найти вероятности каждого из событий В1 и В2. События А1 и А2 независимы, следовательно, независимы события А1 и , а также и А2, поэтому применима теорема умножения:

Подставив эти вероятности в соотношение (*), найдем искомую вероятность появления только оного из событий А1 и А2:

Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того что при аварии сигнализатор сработает, равна 0.95 для первого сигнализатора и 0.9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

Введем обозначения событий: — появилось только событие ( Срабатывание первого сигнализатора); — появилось только событие( Срабатывание второго сигнализатора).

Появление события равносильно появлению события (появилось первое событие и не появилось второе), т. е.. Появление события Равносильно появлению события (появилось второе событие и не появилось первое), т. е. . Таким образом, чтобы найти вероятность появления только одного из событий и , достаточно найти вероятность появления одного, безразлично какого, из событий и . События и несовместны, поэтому применима теорема сложения:

Остается найти вероятности каждого из событий и . События и независимы, следовательно, независимы события и , а также и , поэтому применима теорема умножения:

Подставив эти вероятности в соотношение , найдем искомую вероятность появления только одного из событий и .

Вероятность попадания при одном выстреле для первого стрелка равна , значит вероятность промаха – . Для второго – , а промаха – . Потому вероятность того, что при одном залпе в мишень попадет только один из стрелков .

Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.

Из данных задачи следует, что PA2=0,8; PB1+B2=0,38; где A1 и A2 – события попадания в цель первого и второго орудия соответственно. B1и B2 — попадание только одного из соответствующих орудий, т. е. B1 = A1*A2 и B2 = A2*A1 . Обозначим как PA1=p. Так как PB1+B2=PB1+ PB2, то подставляя, получим:

Вероятность поражения цели при одном выстреле первым из орудий составляет – 0,7.

Обозначим за событие, что изделие 1 — стандартно

Обозначим за событие, что изделие 2 — стандартно

Событие Ā1 означает, что изделие 1 — нестандартно

Событие Ā2 означает, что изделие 2 — нестандартно

Тогда по теореме умножения вероятностей получаем, что вероятность того, что первое изделие стандартно, а второе – нет, равна 0,09

(= P(*Ā2)=P()*P(Ā2)=0.9*0.1=0.09)

Соответственно вероятность обратного события (изделие 2 – стандартно, а изделие 1 — нестандартно) такая же

(= P*Ā1)=P()*P(Ā1)=0.9*0.1=0.09)

Тогда по теореме сложения вероятностей несовместных событий получаем, что вероятность того, что одно изделие стандартно, а другое – нет, равна 0,18

(P((*Ā2)+*Ā1))= P(*Ā2)+ P*Ā1)=+=0.09+0.09=0.18)

Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит точность.

Обозначим допущение ошибки, превышающей заданную точность, в измерениях 1,2 и 3 как А1, А2 и А3 соответственно. Так как эти события независимы, то по теореме умножения вероятностей независимых событий искомая вероятность будет вычисляться по формуле:

Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта.

Решение: Обозначим появления товаров высшего сорта 1, 2 и 3 как А1, А2 и А3 соответственно. Так как эти события независимы, то по теореме умножения вероятностей независимых событий искомая вероятность будет вычисляться по формуле:

Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время работы t безотказно будут работать:

А) только один элемент;

Б) только два элемента;

В) все три элемента.

Введем обозначение событий: безотказно работало первое устройство — A1; безотказно работало второе устройство — А2; безотказно работало третье устройство — A3.

B1 – безотказно работала за время t первое устройство A1; B2 – безотказно работало за время t второе устройство А2; B3 – безотказно работало за время t третье устройство A3.

А) Появление события B1 равносильно появлению события A1; равносильно появлению события A2 ; равносильно появлению A3 .

Таким образом, чтобы найти вероятность появления только одного из событий , достаточно найти вероятность появления одного, безразлично какого, из событий , и . События , и Несовместы, поэтому применима теорема сложения:

P () = P()+ P()+ P(). (*)

Остается найти вероятности каждого из событий, и . События , независимы, поэтому применима теорема умножения:

P () =P (A1) =;

P () =P (A2) =;

P () =P (A3) =.

Подставив эти вероятности в соотношение (*), найдем искомую вероятность появления только одного из событий , :

P () =+

Б) Появление события B1 равносильно появлению события A1; равносильно появлению события A1 ; равносильно появлению A3 .

Аналогично предыдущему решению:

P () =+

0,6*0,7*0,2+0,6*0,3*0,8+0,4*0,7*0,8=0,452.

В) Пусть — безотказная работа всех устройств. Тогда событие B равносильно появлению , поэтому

P(B)=P()==0,6*0,7*0,8=0,336.

Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвёртом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится: а) не более чем в трёх ящиках; б) не менее чем в двух ящиках.

— детали нет ни в одном из ящиков, — деталь содержится в одном ящике, — в двух, — в трёх, — в четырёх. Эти события несовместны и образуют полную группу, поэтому .

А) .

Искомая вероятность равна вероятности того, что деталь содержится не во всех четырёх ящиках.

Б) .

Брошены три игральные кости. Найти вероятность следующих событий: а) На каждой из выпавших граней появиться пять очков; б) на всех выпавших гранях появиться одинаковое число очков.

А) Вероятность выпадения на одной игральной кости пяти очков равна p=1/6 .

Тогда вероятность совместного появления 3 одинаковых событий равна P(A)=p*p*p=1/216.

Б) Из первого решения видно, что вероятность появления на каждой из 3 граней одного определенного очка равна P(A)=p*p*p=1/216. Так как таких вариантов 6 ( по числу граней кости), то вероятность появления одинаковых очков равна P(B)=6*P(A)=6*1/216=1/36.

Брошены три игральные кости. Найти вероятности следующих событий: а) на двух выпавших гранях появится одно очко, а на третьей грани – другое число очков; б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани – другое число очков; в) на всех выпавших гранях появится разное число очков.

А) Вероятность того, что на выпавших двух гранях появится одно очко, равна А вероятность того, что на другой грани появится другое количество очков, равна

Искомую вероятность найдем по теореме умножения вероятностей: .

Б) Вероятность того, что на некоторых двух гранях выпадет одинаковое число очков, равна , а вероятность того, что на третьей грани выпадет другое число очков, равна . Искомую вероятность найдем по теореме умножения вероятностей

В) Количество благоприятствующих исходов равно общее количество элементарных исходов равно , искомая вероятность равна: .

Сколько надо бросить игральных костей, чтобы с вероятностью, меньшей , можно было ожидать, что ни на одной из выпавших граней не появится шесть очков?

Введем обозначения событий: — ни на одной из выпавших граней не появится 6 очков; – на выпавшей грани Кости не появится 6 очков.

Интересующее нас событие состоит в совмещении событий , , …, , т. е.

Вероятность того, что на любой выпавшей грани появится число очков, не равное шести, равна

События независимы в совокупности, поэтому применима теорема умножения:

По условию, . Следовательно, . Отсюда, учитывая, что , найдем: . Таким образом, искомое число игральных костей

В урне имеется 5 шаров с номерами от 1 до 5. Наудачу по одному извлекаются 3 шара без возвращения. Найти вероятность следующих событий: а) последовательно появятся шары с номерами 1, 4, 5; б) извлеченные шары будут иметь номера 1, 4, 5 независимо от того, в какой последовательности они появились.

А) введем обозначение событий: А – выпал шар с номером 1, В – выпал шар с номером 4, С – выпал шар с номером 5. Вероятность наступления события А – Р(А) = . Вероятность наступления события В при условии, что событие А уже наступило — (В) = , вероятность события С при условии А, В — (С) = . Искомая вероятность того, что последовательно выпадут шары с номерами 1, 4, 5 по правилу умножения равна произведению вероятностей событий А, В, С : Р = = ≈ 0, 016

Б) вероятность того, что шары с номерами 1, 4, 5 выпадут в произвольной последовательности равна произведению вероятностей событий А, В, С и количества возможных последовательностей, которые могут составить номера шаров : Р = =

Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.

Введём обозначения событий: А – студент знает ответ на первый вопрос, В – студент знает ответ на второй вопрос, С – студент знает ответ на третий вопрос. Вероятность события А равна отношению количества вопросов которые знает студент, к общему количеству вопросов: Р(А) = = . Вероятность события В при условии А — (В) = , вероятность С при условии А, В — (С) = . Вероятность того, что студент знает все три вопроса по правилу умножения вероятностей равна : Р = = ≈ 0, 23.

В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3 , если кубики извлекаются: а) без возврата; б) с возвратом (извлеченный кубик возвращается в мешочек).

A) введем обозначение событий: А – выпал кубик с номером 1, В – выпал кубик с номером 2, С – выпал кубик с номером 3. Вероятность наступления события А – Р(А) = . Вероятность наступления события В при условии, что событие А уже наступило — (В) = , вероятность события С при условии А, В — (С) = . Искомая вероятность того, что при вынимании без возврата выпадут кубики с номерами 1, 2, 3 по правилу умножения равна произведению вероятностей событий А, В, С : Р = = .

Б) вероятность того, что выпадут кубики с номерами 1, 2, 3 при вынимании их с возвращением обратно равна произведению равных вероятностей событий А, В, С:

Р = = .

По данным переписи населения (1981г.) Англии и Уэльса установлено: темноглазые отцы и темноглазые сыновья составили 5% обследованных лиц, темноглазые отцы и светлоглазые сыновья — 7,9%, Светлоглазые отцы и темноглазые сыновья – 8,9%, Светлоглазые отцы и светлоглазые сыновья – 78,2%. Найти связь между цветом глаз отца и сына.

По условию,

Найдем условную вероятность того, что сын темноглазый если отец темноглазый:

Найдем условную вероятность того, что сын светлоглазый, если отец темноглазый:

Найдем условную вероятность того, что сын темноглазый, если отец светлоглазый:

Найдем условную вероятность того, что сын светлоглазый, если отец светлоглазый:

Найти вероятность Р(А) по данным вероятностям:

Р(АВ)=0,72, Р(А)=0,18.

Событие А можно представить в виде суммы следующих двух несовместных событий:

А=АВ+ А. По теореме сложения вероятностей несовместных событий получим

Р(А)= Р(АВ+ А)=Р(АВ)+Р(А)=0,72+0,18=0,9.

Найти вероятность по данным вероятностям: , , .

Используя тождество найдём

(*)

Из равенства выразим :

(**)

Подставив (**) в (*), получим

Задание: Найти вероятность по данным вероятностям:

Используя тождество , найдем :

Подставив в последнее равенство (см. задачу 73), получим:

Наступление события необходимо влечёт наступление события . Доказать, что

По условию, наступление события АВ влечёт наступление события, поэтому. (*)

Используя тождества , ,

И учитывая неравенство (*), получим

Доказать, что PA(B)≥1 — P(B)/P(A). Предполагается, что P(A)>0.

Справедливо неравенство: P(A) + P(B) — P(AB) ≤1.

Воспользуемся тождествами: P(AB) = P(A)*PA(B), P(B) = 1 – P(B).

Подставив P(AB)=P(A)*PA(B), P(B) =1– P(B) в P(A) + P(B)- P(AB) ≤1,

Получим P(A) + 1 – P(B) – P(A)*PA(B) ≤1, или

Разделив обе части неравенства на положительное число P(A), окончательно имеем:

По условию, наступление события необходимо влечет наступление события , следовательно (см. задачу 48), . Таким образом, если будет доказано неравенство (*), то будет справедливо и неравенство, указанное в условии задачи.

Докажем неравенство (*). Воспользуемся тождествами:

(**)

Из трех событий ,, можно составить следующую полную группу «сложных событий», состоящих из появлений и непоявлений рассматриваемых трех событий:

— появились все три события,

, , – появилось одно событие, а два других не появились,

– не появились все три события.

Сумма вероятностей событий, образующих полную группу, равна единице, поэтому

. (***)

Подставив (**) в (*) и используя (***), после упрощений получим

Учитывая, что каждое слагаемое в квадратной скобке неотрицательно, окончательно получим

Вывести теорему сложения вероятностей для трех совместных событий:

P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).

Предполагается, что для двух совместных событий теорема сложения уже доказана:

P(A1 + A2) = P(A1) + P(A2) – P(A1A2).

Сведем сумму трех событий к сумме двух событий: А + В + С = (А + В) + С.

Воспользуемся теоремой сложения вероятностей двух событий:

Р(А + В + С) = Р[(А + В) + С] = Р(А + В) + Р(С) — Р[(А + В)*С] = Р(А + В) + Р(С) — Р[(А*С) + (В*С)]

Применим теорему сложения вероятностей двух совместных событий дважды (для событий А и В, а также для событий АС и ВС):

Учитывая, что Р[(АС)(ВС)] = Р(АВС), окончательно получим P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).

Даны три попарно независимых события A, B, C, которые, однако, все три вместе произойти не могут. Предполагая, что все они имеют одну и ту же вероятность p, найти наибольшее возможное значение p.

Так как события попарно независимы и , также верно .

Обозначим . Выразим через , пользуясь теоремой сложения для трёх несовместных событий:

Решив это уравнение относительно , получим .

В таком случае достигает максимального значения (при ).

Если , то, на первый взгляд, . Покажем, что допущение приводит к противоречию. Действительно, при условии, что ; или, так как , при условии, что . Отсюда .

Итак, наибольшее возможное значение .

Вероятность отказа первого элемента равна 0,1,второго — 0,15,третьего – 0,2. То есть =0,1, =0,15, =0,2

=0,9, =0,85, =0,8

Тока в цепи не будет, если откажет хотя бы один элемент

То есть нужно использовать формулу появления хотя бы одного события (P(A)=1-*…*)

Значит, искомая вероятность равна 0,388

(P(A)=1-**=1-(0,9*0,85*0,8)=0,388)

Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

Вероятность того, что откажет 1й элемент, 2й элемент или оба, обратна вероятности того, что ни один не откажет, т. е.:

Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.

При последовательном сбрасывании четырех бомб мост будет разрушен (событие А), если в него попадет хотя бы одна бомба. Следовательно, искомая вероятность равна:

Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку.

Вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку равна:

Р(А) = 1 — q1q2q3 = 1 –(1 – 0,1)*(1 – 0,15)*(1 – 0,2) = 0,388.

Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым полу — получает приз. Найти вероятность получения приза спортсменами.

Для вручения приза достаточно, чтобы хотя бы одна из четырех попыток была успешной. Вероятность успешной попытки р = 0,5, а неуспешной q=1 — 0,5 = 0,5. Искомая вероятность

Р = 1 — q^4 = 1 —0,5^4 =0,9375.

Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.

Для получения приза достаточно, чтобы хотя бы одна из четырех попыток была успешна. Вероятность успешной попытки p=0,3 , неуспешной q=1-p=0,7. Тогда искомая вероятность будет равна P=1-q*q*q*q=1-≈0,76

Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.

Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна

Р(А)=1-q3, где q — вероятность промаха. По условию, P (A) = 0,875. Следовательно,

0,875=1—q3, или q3 = 1—0,875 = 0,125.

Отсюда q= =0,5.

Искомая вероятность р = 1— q = 1—0,5 = 0,5.

Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна

Р(А)=1-q4, где q — вероятность промаха. По условию, P (A) = 0,9984.

0,9984=1—q4, или q4 = 1—0,9984= 0,0016.

Отсюда q= =0,2.

Искомая вероятность р = 1— q = 1—0,2 = 0,8.

Многократно измеряют некоторую физическую величину. Вероятность того, что при считывании показаний прибора допущена ошибка, равна . Найти наименьшее число измерений, которое необходимо произвести, чтобы с вероятностью можно было ожидать, что хотя бы один результат измерений окажется неверным.

Вероятность хотя бы одной ошибки из считываний равна , где , и — вероятность ошибки при одном считывании. Из условия получим: ; ; ;

Следовательно, искомое число измерений равно , где – целая часть числа

В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).

Обозначим через А событие — извлечен белый шар. Возможны следующие предположения о первоначальном составе шаров: В1 — белых шаров нет, В2 — один белый шар, В3 — два белых шара.

Поскольку всего имеется три гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице (так как они образуют полную группу событий), то вероятность каждой из гипотез равна 1/3, т. е. P(B1) = P(B2) = P(B3) =

Вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, . Если в урне был один белый шар, то . Условная вероятность того, что будет извлечен белый шар, при условии, что в урне было два белых шара

Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:

Ответ: P(A)=

В урну, содержащую n шаров, опущен белый шар, после наудачу извлечен один шар. Найти вероятность того что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров по цвету.

Обозначим через А событие — извлечен белый шар. Возможны следующие предположения о первоначальном составе шаров: В1- 1 белый шар, В2- 2 белых шара. Вn-n белых шаров. Поскольку всего имеется n гипотез, причем по условию они равновозможны и сумма вероятностей равна единице, то вероятность каждой гипотезы равна . По гипотезе В1 условная вероятность вытащить белый шар равна , по гипотезе В2 условная вероятность вытащить белый шар равна … по гипотезе Вn условная вероятность вытащить белый шар равна .

Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:

В вычислительной лаборатории имеется шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна ; для полуавтомата эта вероятность равна . Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.

Обозначим через событие – произведен расчет на наудачу выбранной машине. Возможны следующие гипотезы в данном эксперименте: — расчет производится на клавишном автомате, — расчет производится на полуавтомате.

Так как имеется 6 клавишных автоматов и 4 полуавтомата, то вероятность того, что произойдет гипотеза , равна . А вероятность того, что произойдет гипотеза , равна .

Условная вероятность того, что клавишный автомат не выйдет из строя, равна , т. е . А условная вероятность того, что полуавтомат не выйдет из строя, равна , т. е .

Искомая вероятность того, что до окончания эксперимента машина не выйдет из строя, находим по формуле полной вероятности:

В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

A – стрелок поразит мишень

В1 – взятая наудачу винтовка снабжена оптическим прицелом

В2 – взятая наудачу винтовка без оптического прицела

Следовательно, по условию, вероятность события А при условии события В1: , а вероятность события А при условии события В2: .

В свою очередь вероятность события В1: , т. к. всего винтовок 5, а благоприятствуют событию 3 винтовки. Аналогично .

Пользуясь формулой полной вероятности

, получим:

Задание: В ящике содержится 12 деталей, изготовленных на заводе № 1, 20 деталей —на заводе № 2 и 18 деталей— на заводе № 3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,9; для деталей, изготовленных на заводах N° 2 и № 3, эти вероятности соответственно равны 0.6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.

Обозначим через A событие – извлечена деталь отличного качества. Возможно три варианта гипотезы: – извлечена деталь отличного качества, изготовленная заводе №1; – извлечена деталь отличного качества, изготовленная заводе №2; – извлечена деталь отличного качества, изготовленная заводе №3. По условию

Найдём вероятности того, что извлечённая деталь изготовлена на заводе №1, №2, №3.

Где — общее число изготовленных на 3-х заводах деталей, – количество деталей изготовленных, соответственно, на заводах №1, 2, 3.

Искомая вероятность вероятность того, что извлеченная наудачу деталь окажется отличного качества находится по формуле полной вероятности:

В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.

Обозначим через событие – извлечён белый шар. Возможны следующие гипотезы:

— белый шар взят из первой урны,— белый шар взят из второй урны.

Поскольку всего имеется две гипотезы, причём по условию они равновероятны, и сумма вероятностей гипотез равна единице(т. к. они образуют полную группу событий), то вероятность каждой из гипотез равна , т. е. .

Условная вероятность того, что белый шар будет извлечён из первой урны равна: =

Условная вероятность того, что белый шар будет извлечён из второй урны равна: =

По формуле полной вероятности находим:

В каждой из трех урн содержится 6 черных 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.

A1 – вероятность того, что из первой урны извлечен белый шар.

A2 – вероятность того, что из первой урны извлечен черный шар.

B1 – вероятность того, что из второй урны извлечен белый шар, после того как из первой урны переложили во вторую урну белый шар.

B2 – вероятность того, что из второй урны извлечен белый шар, после того как из первой урны переложили во вторую урну черный шар.

C1 – вероятность того, что из второй корзины будет извлечен белый шар.

C2 – вероятность того, что из второй корзины будет извлечен черный шар.

D1 – вероятность того, что из третьей урны извлечен белый шар, после того как из второй урны переложили в втретью урну белый шар.

D2 – вероятность того, что из третьей урны извлечен белый шар, после того как из второй урны переложили в втретью урну черный шар.

E – вероятность того, что из третьей урны будет извлечен белый шар.

Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.

Пусть А – событие того, что сбой будет обнаружен, тогда из формулы полной вероятности следует, что:

PA= PB1PB1A+PB2PB2A+PB3PB3A= 0,3*0,8+0,2*0,9+0,5*0,9=0,87.

Обозначим через А событие – деталь отличного качества

Можно сделать два предположения

-деталь произведена первым автоматом (так как производительность первого автомата вдвое больше второго автомата, то Р()=2/3)

-деталь произведена вторым автоматом (Р()=1/3)

Условная вероятность, что она будет отличного качества, если она произведена первым автоматом (A)=0,6

Условная вероятность, что она будет отличного качества, если она произведена первым автоматом (A)=0,84

Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна

P(A)=Р()*(A)+ Р()*(A)=2/3*0.6+1/3*0.84=0.68

Вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна

()===

Ответ:

В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?

Обозначим событие А – стрелок поразил мишень и гипотезы: B1 – стрелок выбрал винтовку с оптическим прицелом, B2 – без оптического прицела. Тогда . Условные вероятности попадания из винтовки с оптическим прицелом и без: . Вычислим вероятность попадания из наудачу взятой винтовки:

Теперь, воспользовавшись формулой Бейеса, получим ответ:

Ответ: Стрелок вероятнее всего стрелял из винтовки без оптического прицела.

Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

Обозначим через А событие—подъезд автомобиля к заправке. Можно сделать два предположения: —проехал грузовой автомобиль, причем =3/5; — проехал легковой автомобиль, причем = 2/5.

Условная вероятность, что проезжающий грузовой автомобиль подъедет на заправку: = 0,1 . Для легкового: = 0,2.

Вероятность того, что проезжающий автомобиль подъедет на заправку, по формуле полной вероятности равна Р(А) = + = 3/5 0,1 + 2/5 0,2 = 0,14

Искомая вероятность того, что подъехавший к заправке автомобиль будет грузовым, по формуле Бейеса равна = = = 3/7

Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора были исправны.)

Обозначим через событие А – ошибку перфораторщицы. Тогда, – ошибка сделана первой перфораторщицей, — ошибка сделана второй перфораторщицей. Причем P()=0,5 и P()=0,5, т. к. обе работали одинаково.

Условная вероятность того, что первая перфораторщица допустит ошибку, равна (A)=0,05;

Условная вероятность того, что вторая перфораторщица допустит ошибку, равна (A)=0,1.

Вероятность того, что наудачу взятая перфокарта, окажется с ошибкой равна, по формуле полной вероятности равна:

P(A)= P()*(A)+ P()*(A)=0,5*0,05+0,5*0,1=.

Искомая вероятность того, что взятая перфокарта произведена первой перфораторщицей, по формуле Бейеса равна:

===.

В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30%—с заболеванием L, 20%—с заболеванием М — Вероятность полного излечения болезни К равна 0,7; для болезней L и М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К.

Больные поступают в больницу в разном процентном соотношении. Р(k)= 0.7, P(L)=0.3,P(M)= 0.2, где K, L,M – заболевания, а Р(Х)- вероятность поступления с данным заболеванием. Тогда Pk(A)=0.7, Pl(A)=0.8 ,Pm(A)=0.9 это вероятность полного излечения от данного заболевания. Чтобы найти вероятность что Больной, поступивший в больницу, был выписан здоровым надо найти :

P(A)= Pk(a)*P(k) + Pl(a)*P(l) + Pm(a)*P(m) = 0.7*0.5 + 0.8*0.3 + 0.9*0.2 = 0.77

А вероятность что больной страдал именно заболеванием К равно:

Pa(K) = (Pk(a)*P(k))/P(A)= (0.5*0.7)/0.77 = 5/11

Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равно 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.

Обозначим через А – изделие признана стандартной. — вероятность того, что изделие попало к первому товароведу. — ко второму. P() = 0,55 , P() = 0,45.

Условная вероятность того что изделие будет признано стандартным первым товароведом равна (A) = 0,9, вторым — (A) = 0,98.

Вероятность того, что изделие будет признано стандартным по формуле полной вероятности равна

P(A)= P() (A) + P() (A) = 0,55 * 0,9 + 0,45 * 0,98 = 0,936

Искомая вероятность того, что изделие проверил второй товаровед, по формуле Бейеса равна

()= P() * (A) / P(A)= 0,45*0,98 / 0,936 = 0,47.

Событие А может появится при условии появления одного из несовместимых событий В1, В2,…, Вn, образующих полную группу событий. После появления события А были переоценены вероятности гипотез, то есть были найдены условные вероятности РА(Вi) (i=1,2,…,n). Доказать, что сумма РА(Вi) (i=1,2,…,n) равна 1.

По формуле Бейеса:

Что и требовалось доказать.

Событие может появиться при условии появления одного из несовместных событий (гипотез) , образующих полную группу событий. После появления события были переоценены вероятности этих гипотез, т. е. были найдены условные вероятности этих гипотез, причем оказалось, что . Чему равна условная вероятность гипотезы ?

Так как события образуют полную группу, и появится при условии появления лишь одного из них, то верно . Так как имеем , то:

Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.

Обозначим через А событие – в каждом из двух испытаний была извлечена стандартная деталь. Можно предположить, что B1 – детали извлекались из первой партии; B2 – детали извлекались из второй партии; В3 – детали извлекались из третей партии.

Детали извлекались на удачу, поэтому вероятности предположений одинаковы:

P(B1) = P(B2) = P(B3) =

Вероятность того, что из первой партии будут последовательно извлечены две стандартные детали; поэтому

Условная вероятность т. е вероятность того, что из второй партии будут извлечены две стандартные детали:

Найдем условную вероятность т. е вероятность того, что из третей партии будут последовательно извлечены две стандартные детали:

Искомая вероятность того, что обе извлеченные детали стандартные взяты из третей партии, по формуле Бейеса равна

Ответ:

Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны , , .

Обозначим через A событие — два орудия попали в цель. Сделаем два предположения: — орудие не попало в цель.

По условию , следовательно

Найдем условную вероятность , т. е. вероятность того, что в цель попало 2 снаряда, причем один из них послан первым орудием и, следовательно, второй — либо вторым орудием, либо третьим. Эти два события несовместны, поэтому применима теорема сложения:

Найдем условную вероятность , т. е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах. Другими словами найдем вероятность того, что второе и третье орудие попали в цель. Эти два события независимы, поэтому применима теорема умножения:

Искомая вероятность того, что первое орудие дало попадание, по формуле Бейеса равна:

Ответ:

Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.

Обозначим через А событие – две пули поразили мишень. Сделаем два предположения (гипотезы): В1 – третий стрелок поразил мишень; В2 – третий стрелок не попал в мишень.

По условию, Р(В1) = 0,4; следовательно (событие В2 противоположно событию В1),

Найдем условную вероятность РВ1(А), т. е. вероятность того, что мишень поразили две пули, причем одна из них принадлежит третьему стрелку и, следовательно, вторая – либо первому стрелку (при этом второй не попал), либо второму стрелку (при этом первый не попал). Эти два события несовместны, поэтому применима теорема сложения:

РВ1(А) = p1∙q2 + p2∙q1 = 0,6∙0,5 + 0,5∙0,4 = 0,5.

Найдем условную вероятность РВ2(А), т. е. вероятность того, что мишень поразили две пули, причем третий стрелок промахнулся. Другими словами, найдем вероятность того, что первый и второй стрелки поразили мишень. Эти два события независимы, поэтому применима теорема умножения:

РВ2(А) = p1∙p2 = 0,6∙0,5 = 0,3.

Искомая вероятность того, что третий стрелок поразил мишень, по формуле Бейеса равна

Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2; 0,4 и 0,3.

Обозначим через А событие – отказали два элемента. Можно сделать следующие предположения (гипотезы):

В1 — отказали первый и второй элементы, а третий элемент исправен, причем (поскольку элементы работают независимо, применима теорема умножения)

Р(В1) = p1∙p2∙q3 = 0,2∙0,4∙0,7 = 0,056;

В2 — отказали первый и третий элементы, а второй элемент исправен, причем

Р(В2) = p1∙p3∙q2 = 0,2∙0,3∙0,6 = 0,036;

В3 — отказали второй и третий элементы, а первый — исправен, причем

Р(В3) = p2∙p3∙q1 = 0,4∙0,3∙0,8 = 0,096;

В4 — отказал только один элемент; В5 — отказали все три элемента; В6 — ни один из элементов не отказал.

Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности РВ4(А), РВ5(А) и РВ6(А) равны нулю, следовательно, равны нулю и произведения Р(В4)∙РВ4(А), Р(В5)∙РВ5(А) и Р(В6)∙РВ6(А) при любых значениях вероятностей гипотез В4, В5 и В6.

Поскольку при гипотезах В1, В2 и В3 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = 1.

По формуле полной вероятности, вероятность того, что отказали два элемента, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) = 0,056 + 0,036 + 0,096 = 0,188.

По формуле Бейеса, искомая вероятность того, что отказали первый и второй элементы,

РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,056/0,188 = 0,3.

Две из четырех независимо работающих ламп прибора отказали. Найти вероятность того, что отказали первая и вторая лампы, если вероятности отказа первой, второй, третьей и четвертой ламп соответственно равны 0,1, 0,2, 0,3 и 0,4.

Обозначим через А событие – отказали две лампы. Можно сделать следующие предположения (гипотезы):

В1 — отказали первая и вторая лампы, а третья и четвертая лампы исправны, причем (поскольку лампы работают независимо, применима теорема умножения)

Р(В1) = p1∙p2∙q3∙q4 = 0,1∙0,2∙0,7∙0,6 = 0,0084;

В2 — отказали первая и третья лампы, а вторая и четвертая исправны, причем

Р(В2) = p1∙q2∙p3 ∙q4 = 0,1∙0,8∙0,3∙0,6 = 0,0144;

В3 — отказали первая и четвертая лампы, а вторая и третья — исправны, причем

Р(В3) = p1∙q2∙q3∙p4 = 0,1∙0,8∙0,7∙0,4 = 0,0224;

В4 — отказали вторая и третья лампы, а первая и четвертая — исправны, причем

Р(В4) = q1∙p2∙p3∙q4 = 0,9∙0,2∙0,3∙0,6 = 0,0324;

В5 — отказали вторая и четвертая лампы, а первая и третья — исправны, причем

Р(В5) = q1∙p2∙q3∙p4 = 0,9∙0,2∙0,7∙0,4 = 0,0504;

В6 — отказали третья и четвертая лампы, а первая и вторая — исправны, причем

Р(В6) = q1∙q2∙p3∙p4 = 0,9∙0,8∙0,3∙0,4 = 0,0864;

В7 – отказала только одна лампа; В8 — отказали три лампы; В9 — отказали все четыре лампы и В10 – все лампы остались исправны.

Вероятности последних четырех гипотез не вычислены, так как при этих гипотезах событие А (отказали две лампы) невозможно и значит условные вероятности РВ7(А), РВ8(А), РВ9(А) и РВ10(А) равны нулю, следовательно, равны нулю и произведения Р(В7)∙РВ7(А), Р(В8)∙РВ8(А), Р(В9)∙РВ9(А) и Р(В10)∙РВ10(А) при любых значениях вероятностей гипотез В7, В8, В9 и В10.

Поскольку при гипотезах В1 – В6 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = РВ4(А) = РВ5(А) = РВ6(А) = 1.

По формуле полной вероятности, вероятность того, что отказали две лампы, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) + Р(В7)∙РВ7(А) + Р(В8)∙РВ8(А) + Р(В9)∙РВ9(А) + Р(В10)∙РВ10(А) = 0,0084 + 0,0144 + 0,0224 + 0,0324 + 0,0504 + 0,0864 = 0,2144.

По формуле Бейеса, искомая вероятность того, что отказали первая и вторая лампы, равна

РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,0084/0,2144

Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести (ничьи во внимание не принимаются)?

Играют равносильные шахматисты, поэтому вероятность выигрыша p=1/2; следовательно, вероятность проигрыша q также равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.

Найдем вероятность того, что две партии из четырех будут выиграны:

Найдем вероятность того, что выиграны три партии из шести:

Так как P4(2)>P6(3), то вероятнее выиграть две партии из четырех, чем три из шести.

Два равносильных противника играют в шахматы. Что вероятнее: а) Выиграть одну партию из двух или две партии из четырех? б)выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаються.

Играют равносильные шахматисты, поэтому вероятность выигрыша ; следовательно, вероятность проигрыша . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигранв партии, то применима формула Бернулли.

А) Найдем вероятность того, что две партии из четырех будут выиграны:

Найдем вероятность того, что одна партия из двух будет выиграна:

Б) Найдем вероятность выиграть не менее двух партий из четырех:

Найдем вероятность выиграть не менее трех партий из пяти:

Монету бросают пять раз. Найти вероятность того, что “герб” выпадет: а)мене двух раз; б)не менее двух раз.

При бросании монеты вероятность выпадения герба и решки, равновероятны, поэтому вероятность выпадения герба равна ; следовательно вероятность выпадения решки ; Так как при бросании вероятность постоянна, то применима формула Бернулли.

А) Найдем вероятность того, что герб выпадет менее двух раз:

;

Б) Найдем вероятность того, что герб выпадет не менее двух раз:

;

Ответ: a) ; б)

А) Найти вероятность того, что событие А появится не менее трёх раз в четырёх независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4;

Б) Событие В появится в случае, если событие А наступит не менее четырёх раз. Найти вероятность наступления события В, если будет произведено 5 независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

А)Так как вероятность появления события А во всех испытаниях одинакова и все испытания независимы, то применяем формулу Бернулли. Так как вероятность появления события А в одном испытании равна 0,4, т. е. р = 0,4, то вероятность не появления события А в одном испытании равна

Найдём вероятность того, что событие А появится ровно 3 раза в четырёх независимых испытаниях и найдём вероятность того, что событие А появится ровно 4 раза в четырёх независимых испытаниях и просуммируем их:

Б) Так как вероятность появления события А во всех испытаниях одинакова и все испытания независимы, то применяем формулу Бернулли.

Найдём вероятности того, что событие А появится ровно 4 раза и 5 раз в пяти независимых испытаниях и просуммируем:

Ответ: а) 0,1792 б) 0,73728

Задание: Устройство состоит из трех независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t, если: а) работают только основные элементы; б) включен один резервный элемент; в) включены два резервных элемента. Предполагается, что резервные элементы работают в том же режиме, что и основные, вероятность отказа каждого резервного элемента также равна 0,1 и устрой — устройство отказывает, если работает менее трех элементов.

По условию , следовательно вероятность стабильной работы каждого элемента . Так как безразлично какой из элементов откажет и вероятности отказа всех элементов равны, применима формула Бернулли.

А) Найдём вероятность того, что будут работать все 3 элемента:

Б) Найдём вероятность того, что устройство будет работать при одном дополнительном элементе на протяжении времени t. :

В) Найдём вероятность того, что устройство будет работать при двух дополнительных элементах на протяжении времени t. :

В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков в) более двух мальчиков г) не менее двух и не более трёх мальчиков.

Вероятность рождения мальчиков принять равной 0.51

По условию =0.51 следовательно вероятность = 0.49 и применима формула Бернулли.

А) Найдём вероятность того, что в семье 2 мальчика:

0.62

Б) Найдём вероятность того, что в семье не более двух мальчиков:

В) Найдём вероятность того, что в семье более двух мальчиков:

Г) найдём вероятность того, что в семье не менее двух и не более трёх мальчиков:

На отрезок АВ длины а наудачу брошено пять точек. Найти вероятность того, что две точки будут находиться от точки А на расстоянии, меньшем x, а три — на расстоянии, большем x. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

Т. к. p = xa — вероятность того, что точка будет находиться на расстоянии меньшем чем x, следовательно, q = 1 – p=1- xa= a-xa. По формуле Бернулли имеем: Pnk= Cnkpkqn-k. P52= C52xa2a-xa3.

Отрезок разделен на четыре равные части. На отрезок наудачу брошено восемь точек. Найти вероятность того, что на каждую из четырех частей отрезка попадет по две точки. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

Вероятность того, что точка попадет в нужный отрезок равна р=1/4.

Искомая вероятность равна

Р= С82 С62 С42 С22*(1/4)8

Найти вероятность того, что событие A наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

По условию, n=243; k=70; p=0,25; q=0,75. Т. к. n=243 – достаточно большое число, воспользуемся локальной теоремой Лапласа:

Найдем значение x: . По таблице найдем

Тогда искомая вероятность

Ответ: .

Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.

По условию, n=2400; k=1400; p=0,6; q=0,4. Так как n=2400 – достаточно большое число, воспользуемся локальной теоремой Лапласа:

Найдем значение x: .

Так как четная функция, то = .

По таблице найдем

Тогда искомая вероятность

Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.

Так как n велико, воспользуемся локальной теоремой Лапласа:

(k)=φ(x).

X===-1,25.

Функция φ(x) четная, поэтому φ(-1,25)= φ(1,25)=0,1826.

Монета брошена 2N раз (N велико!). Найти вероятность того, что «герб» выпадет ровно N раз.

N=2N, k=N, p=0,5, q=0,5. Для нахождения вероятности выпадения «герба» ровно N раз воспользуемся локальной теоремой Лапласа :

(N)=φ(x)* 1/;

φ(x)=1/;

X=(k-pn)/;

X=0; φ(x)≈0,3989; (N)≈0.5641/

Монета брошена 2N раз. Найти вероятность того, что «герб» выпадет на 2m раз больше, чем надпись.

Т. к. исход каждого испытания не зависит от предыдущих исходов и возможных исходов два («герб» или надпись), то вероятность выпадения «герба» в каждом испытании равна . Всего проведено n=2N испытаний, а «герб» выпал на 2m раза больше, чем надпись, значит обозначим количество выпадений «герба» за t, получим уравнение: . Очевидно, что количество исходов, в которых выпал «герб», равно .

По локальной теореме Лапласа вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, событие наступит ровно k раз, равна:

Вероятность появления события в каждом из независимых испытаний постоянна и равна . Найти вероятность того, что событие появится: а) не менее раз и не более раз; б) не менее раз; в) не более раз.

Воспользуемся интегральной теоремой Лапласа: , где – функция Лапласа,

A) По условию, . Вычислим :

Учитывая, что функция Лапласа нечетна, т. е. , получим:

По таблице приложения найдем:

Б) Требование, чтобы событие появилось не менее раз, означает, что число появления событий может быть равно . Таким образом в рассматриваемом случае следует принять . Тогда:

По таблице приложения найдем:

В) События – « появилось не менее раз» и « появилось не более раз» противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность:

Вероятность появления события в каждом из 2100 испытаний равна 0,7. Найти вероятность того что событие появится не менее 1470 и не более 1500 раз.

Воспользуемся интегральной теоремой Лапласа:

, где Ф(х)- функция Лапласа,

По условию, n= 2100; p=0,7; q=0,3; k1= 1470; k2= 1500;

Тогда ;

По таблице значений функции Лапласа:

Вероятность появления события в каждом из 21 независимых испытаний равна 0,7. Найти вероятность того, что событие появится в большинстве испытаний.

Воспользуемся интегральной теоремой Лапласа:

где и

=(21-14,3/2,1)=(3)=0,4986;

=(11-14,3/2,1)=(-1,7)=0,4532

Так как функция Лапласа нечетная то получим следующее равенство:

==0,4986+0,4532=0,9518

Монета брошена 2N раз (N велико). Найти вероятность того, что число выпадений «герба» будет заключено между числами и .

Воспользуемся интегральной теоремой Лапласа:

, где Ф(х) – функция Лапласа,

По условию задачи n=N; p=0,5; q=0,5, =; =.

Вычислим и :

Задание: Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?

По условию:

Воспользуемся интегральной теоремой Лапласа:

Подставляя данные задачи в формулу, получим

Очевидно, число испытаний , поэтому Поскольку функция Лапласа — возрастающая и , то можно положить . Следовательно,

По таблице приложения 2 найдем . Отсюда и из соотношения (*), учитывая, что функция Лапласа нечетная, получим

Решив это уравнение, как квадратное относительно Получим. Следовательно, искомое число испытаний.

По условию, ; ; ; . Требуется найти вероятность . Воспользуемся формулой

По таблице приложения 2 найдем . Следовательно, .

Итак, искомая вероятность приближенно равна 0,9876.

Вероятность появления события в каждом из 900 независимых испытаний равна 0,5. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.

По условию: n = 900; p = 0,5; q = 0,5; ε = 0,02; Требуется найти вероятность: Pm900- 0,5≤0,02 . Воспользуемся формулой:

Имеем:
Pm900- 0,5≤0,02 =2ϕ0,029000,5*0,5= 2ϕ1,2= 0,7698.

Французский ученый Бюффон бросил монету 4040 раз, причем «герб» появился 2048 раз. Найти вероятность того, что при повторении опыта Бюффона относительная частота появления «герба» отклониться от вероятности появления «герба» по абсолютной величине не более чем в опыте Бюффона.

N=4040; k=2048; p=0,5

Воспользуемся формулой P(|m/n-p| ≤ε) = 2Ф( εnpq ).

ε= |2048/4040 – 0,5|= 0,507 – 0,5= 0,007

X= 0,007 *40400,5*0,5 = 0,89

Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний n, при котором с вероятностью 0,7698 можно ожидать, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.

По условию, р = 0,5; q = 0,5; =0,02;

Р (| m/n-0,5| ≤ 0,02) = 0,7698.

Воспользуемся формулой Р(|m/n — p| ≤ ) = 2Ф ( )

В силу условия 2Ф ( ) = 0,7698

Или Ф(0,04 )=0,3849.

По таблице приложения 2 найдем Ф( 1,2) = 0,3849.

Следовательно, 0,04 = 1,2 или = 30

Таким образом, искомое число испытаний n =900.

Сколько раз нужно бросить игральную кость, чтобы вероятность неравенства

| m/n — 1/6| ≤ 0,01 была не меньше чем вероятность противоположного неравенства, где m—число появлений одного очка в n бросаниях игральной кости?

Воспользуемся формулой Р(|m/n — p| ≤ ) = 2Ф ( )

По условию, р=1/6, q = 5/6, = 0,01. Вероятность осуществления неравенства, противоположного заданному, т. е. неравенства | m/n — 1/6|0,01, равна 1- 2Ф ( )

Согласно условию должно иметь место неравенство

2Ф ( )≥ 1- 2Ф ( )

Или 4Ф ( )≥ 1, отсюда Ф ( )≥ 0,25

По таблице приложения 2 найдем Ф(0,67) =0,2486; Ф(0,68) = 0,2517.

Выполнив линейную интерполяцию, получим Ф (0,6745) =0,25.

Учитывая соотношение (*) и принимая во внимание, что функция Ф (*)— возрастающая, имеем

или 0,01 )≥ 0,6745

Отсюда искомое число бросаний монеты n≥632.

Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти наименьшее число испытаний n, при котором с вероятностью 0,99 можно ожидать, что относительная частота появлений события отклонится от его вероятности по абсолютной величине не более чем на 0,04.

По условию, р = 0,2; q = 0,8; =0,04;

Воспользуемся формулой Р(|m/n — p| ≤ ) = 2Ф ( )

Получим Р(|m/n – 0,2| ≤ 0,04 ) = 2Ф (0,04 )

2Ф (0,04 )=0,99 или Ф(0,1 )=0,495.

По таблице приложения 2 найдем Ф(2,56) =0,4948; Ф(2,58) = 0,4951

Выполнив линейную интерполяцию, получим Ф (2,573) =0,495.

Следовательно 0,01 =2,573

В урне содержатся белые и черные шары в отношении 4:1. После извлечения шара регистрируется его цвет и шар возвращается в урну. Чему равно наименьшее число извлечений n, при котором с вероятностью 0,95 можно ожидать, что абсолютная величина отклонения относительной частоты появления белого шара от его вероятности будет не более чем 0,01?

По условию p=1/5; q=4/5; ξ=0,01; P=0,95; n=?. Воспользуемся формулой

P( |m/n – p| ≤ ξ)= 2Φ(ξ )

Из условия P=0.95=2Φ(ξ ) , отсюда Φ=0,475

0,475=Φ(x)= Φ(ξ ) , Φ=0,475 соответствует значение x=1,95 ( из Приложения 2), тогда

X=1.95= ξ =0,01 * =0,025

В) если число пр—целое, то наивероятнейшее число ko = np.

Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число , чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его верояности не превысила .

По условию, n=400, p=0,8, q=0,2. Следовательно,

По таблице приложения 2 найдём , значит

Ответ:

Вероятность появления события в каждом из независимых испытаний равна . Найти такое положительное число , чтобы с вероятностью абсолютная величина отклонения относительной частоты появления события от его вероятности не превысила .

По условию, .

Следовательно,

По таблице приложения 2 найдем , значит . Отсюда искомое число .

Вероятность появления события в каждом из 10 000 независимых событий равна 0,75. Найти такое положительное число ε, чтобы с вероятностью 0,98 абсолютная величина отклонения относительной частоты появления события от его вероятности 0,75 не превысила ε.

По условию, n = 10 000, p = 0,75, q = 0,25. Следовательно,

2Ф (ε 10 000/(0,75*0,25)) = 0,98 или Ф (231*ε) = 0,49.

Т. к. Ф(2,34) = 0,49, значит 231*ε = 2,34. Отсюда искомое число ε = 0,01.

Отдел технического контроля проверяет на стандартность 900 деталей. Вероятность того, что деталь стандартна равна 0,9. Найти с вероятность 0,95 границы, в которых будет заключено число m стандартных деталей среди проверенных.

По условию, n=900, p=0,9, q=0,1. Следовательно,

По таблице приложения 2 найдём , значит . Отсюда .

Таким образом, с вероятностью 0,95 отклонение относительной частоты стандартных деталей от вероятности 0,9 удовлетворяет неравенству

Отсюда искомое число m стандартных деталей среди 900 проверенных с вероятностью 0,95 заключено в следующих границах .

Ответ: .

Отдел технического контроля проверяет 475 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти с вероятностью 0,95 границы, в которых будет заключено число m бракованных изделий среди проверенных.

По условию, n=475, p=0,05, q=0,95. Следовательно,

По таблице приложения 2 найдём , значит . Отсюда .

Таким образом, с вероятностью 0,95 отклонение относительной частоты бракованных изделий от вероятности 0,05 удовлетворяет неравенству

Отсюда искомое число m бракованных изделий среди 475 проверенных с вероятностью 0,95 заключено в следующих границах .

Ответ: .

Игральную кость бросают 80 раз. Найти с вероятностью 0,99 границы, в которых будет заключено число m выпадений шестёрки.

По условию, n=80, p=1/6, q=5/6. Следовательно,

По таблице приложения 2 найдём , значит . Отсюда .

Таким образом, с вероятностью 0,99 отклонение относительной частоты выпадения шестёрки от вероятности 1/6 удовлетворяет неравенству

Отсюда искомое число m испытаний среди 80 с вероятностью 0,99 заключено в следующих границах .

Ответ: .

Испытывается каждый из элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна . Найти наивероятнейшее число элементов, которые выдержат испытание.

По условию, . Найдем наивероятнейшее число из двойного неравенства:

Подставив данные задачи, получим:

Так как – целое число и поскольку между числами заключено одно целое число, а именно , то искомое наивероятнейшее число

Отдел технического контроля проверяет партию из 10 деталей. Вероятность того, что деталь стандартна, равна 0,75. Найти наивероятнейшее число деталей, которые будут признаны стандартными.

По условию n=10; p=0,75; q=1-p=0,25 . Найдем наивероятнейшее число деталей из неравенства:

Из первого неравенства системы найдем: n≤25,60,4=64;

Из второго неравенства системы имеем: n>24,60,4=61,5;

Итак, искомое число испытаний должно удовлетворять двойному неравенству:62≤n≤64.

По условию ; ; . Воспользуемся двойным неравенством

Подставляя данные задачи, получим систему неравенств для определения неизвестного числа:

, .

Из первого неравенства системы найдем .

Из второго неравенства системы найдем .

Итак, искомое число испытаний должно удовлетворить двойному неравенству .

Чему равна вероятность p наступления события в каждом из 49 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 30?

По условию, n=49, k0=30. Воспользуемся двойным неравенством . Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности p:

Из первого неравенства системы найдем p>0,6. Из второго неравенства системы найдем .

Чему равна вероятность р наступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 25?

По условию n = 39, =25. Воспользуемся двойным неравенством . Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности р:

Из первого неравенства системы найдём p>0,625, из второго неравенства системы найдём .

Итак, искомая вероятность должна удовлетворять двойному неравенству .

Ответ:

Батарея произвела шесть выстрелов по объекту. Вероятность попадания в объект при одном выстреле равна 0,3. Найти: а) наивероятнейшее число попаданий;

Б) вероятность наивероятнеишего числа попаданий; в)вероятность того, что объект будет разрушен, если для этого достаточно хотя бы двух попаданий.

По условию, n=6; р=0,3; q=0,7.

А) Найдем наивероятнейшее число попаданий по формуле

Np—qK 3*3=9 – четное число очков на каждой игральной кости.

P=9/36=1/4 – вероятность выпадения четного числа очков на каждой игральной кости.

Pn(0)=9/16 Pn(1)=6/16 Pn(0)=1/16

В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Обставить закон распределения числа стандартных деталей среди отобранных.

Случайная величина X—число стандартных деталей среди отобранных деталей—имеет следующие возможные значения: X1=0; X2=1; X3=2; Найдем вероятности возможных значений X по Формуле: PX=k= Cnk*CN-nm-kCNm.

(N—число деталей в партии, n— число стандартных деталей в партии, m— число отобранных деталей, k— число стандартных деталей среди отобранных), находим:

🎬 Видео

Расстояние между параллельными плоскостямиСкачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

Проекция точки на плоскость, проекция прямой на плоскость. Параллельные прямые.Скачать

Взаимное пересечение двух плоскостейСкачать

7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Плоскость разграфлена параллельными прямыми находящимися на расстоянии 2а

Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2A. На плоскость наудачу

Ваш ответ

решение вопроса

Похожие вопросы

Теория вероятности (много задач)

🎬 Видео