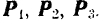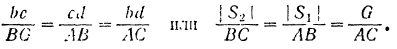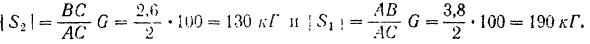| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 |
Министерство образования Российской Федерации
Владивостокский государственный университет
экономики и сервиса
Г. Л. ОВСЯННИКОВА
Рецензент , канд. техн. наук, профессор каф. ФХ и ПМ ВГУЭС
Ч 81 ТЕОРЕТИЧЕСКАЯ МЕХАНИКА: Учебное пособие. Ч. 1. – Владивосток: Изд-во ВГУЭС, 2003 – 128с.
Учебное пособие представляет собой комплекс, содержащий основные сведения о теории, необходимые для самостоятельного решения задач. В каждом разделе даны рекомендации о последовательности решения различных типов задач и приведены подробные методические указания к решению подобных задач. Может использоваться как теоретическая часть при подготовке к сдаче экзамена или зачета, так и в качестве методических указаний к решению задач на практических занятиях, при выполнении контрольных работ заочниками и расчётно-графических заданий.
Для студентов всех форм обучения.
ã Издательство Владивостокского
экономики и сервиса, 2003
- Глава 1. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 1. Сложение двух сходящихся сил
- § 2. Разложение силы на две сходящиеся составляющие
- § 3. Сложение плоской системы сходящихся сил. Силовой многоугольник
- § 4. Проекция силы на ось. Проекция силы на две взаимно-перпендикулярные оси координат
- Разложение силы на сходящиеся составляющие
- Разложение силы на сходящиеся составляющие
- Пример задачи:
- Системы сил
- Плоская система сходящихся сил
- 📸 Видео
Видео:Сложение нескольких векторов. Правило многоугольникаСкачать

Глава 1. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ
Видео:Построение силового многоугольникаСкачать

§ 1. Сложение двух сходящихся сил
Если в одной точке к телу приложены две силы под углом друг к другу, то их сложение выполняется по правилу параллелограмма.
Модуль равнодействующей R может быть определен аналитически из треугольника АВС с помощью теоремы косинусов (рис. 1):
так как 
Направление равнодействующей определяется углами 


откуда, учитывая, что 


Вместо параллелограмма сил можно строить силовой треугольник (рис. 2). Выбрав любую точку на плоскости рисунка, проводят из нее, сохраняя масштаб, вектор, равный и параллельный одной из заданных сил, например F1.
Из конца вектора F1 проводят вектор, равный и параллельный второй силе, F2. Начало первого вектора соединяют с концом второго, замыкая треугольник. Замыкающая сторона треугольника в данном масштабе представляет собой искомую равнодействующую. Модуль и направление равнодействующей определяют аналитически, как было показано выше.
При построении треугольника сил необходимо придерживаться правила: стрелки составляющих векторов направлены в одну сторону, а равнодействующей – им навстречу.
Частные случаи: 1) если 

2) если , т. е. силы действуют по одной прямой в разные стороны, то

3) если 
Заметим, что определение равнодействующей двух сил по правилу параллелограмма или треугольника называется векторным, или геометрическим, сложением.
Задача 1. Определить равнодействующую двух сил 


Задачу можно решить графоаналитическим методом, используя либо правило параллелограмма, либо правило треугольника.
Решение 1 – по правилу параллелограмма:
1. Используя условие задачи и приблизительно соблюдая масштаб, изображаем параллелограмм ABCD (рис. 3, б). Порядок построения такой: из точки А проводим отрезок , затем из той же точки А под углом 120° к отрезку АВ проводим отрезок , из точек В и С проводим прямые BD || АС и CD || AB и, наконец, проводим диагональ
2. Используя формулу (1), можем найти модуль равнодействующей:
Имея в виду, что cos120° = – sin 30° = – 0,5, получаем

3. Применяя к D ABD (или к D ACD) (см. рис. 3, б) теорему синусов, получаем




Таким образом, вектор равнодействующей 
Угол j2 можно найти либо как разность
либо из теоремы синусов:

Один и тот же результат, полученный различными путями, подтверждает правильность решения задачи.
Ответ. Равнодействующая данных сил равна 69,3 Н и линия ее действия образует с направлением силы 
Решение 2 – по правилу треугольника.
1. Используя условие задачи, строим треугольник сил ABC (рис. 3, в). Порядок построения такой: из точки А проведем отрезок 


В получившемся треугольнике
2. Применяем к треугольнику ABC известную из тригонометрии теорему косинусов:
откуда модуль равнодействующей

3. Углы j1 и j2, определяющие направление равнодействующей относительно заданных сил, находим, как и в первом решении, по теореме синусов.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

§ 2. Разложение силы на две сходящиеся составляющие
Любую силу можно рассмотреть как равнодействующую двух произвольных, сходящихся под углом сил. Модуль и направление составляющих сил зависят от угла между ними. Можно построить множество параллелограммов, для которых данная сила R будет служить диагональю (рис. 4). Чтобы задача стала определенной, нужно знать одно из дополнительных условий: модули обеих составляющих, модуль и направление одной из составляющих, направление обеих составляющих, модуль одной из составляющих и направление другой.
Каждую из задач можно решить двумя способами: графическим и графоаналитическим.
При графическом решении задачи заданную силу откладывают на чертеже в выбранном масштабе, а затем производят несложные геометрические построения в зависимости от заданных условий.
Для графоаналитического решения нет надобности соблюдать масштаб, но при построении нужно сохранять примерное направление сил. Модули составляющих сил либо углы, определяющие их направление, вычисляют, пользуясь формулами (1) и (2).
Например, если заданы только направления составляющих сил, то из точки А вектора R (рис. 5) проводим линии действия составляющих AM и AN под известными углами 

При графоаналитическом решении модули сил F1 и F2 определяют по формулам, полученным из выражения (1):


Задача 2. Определить силы, растягивающие нити АВ и ВС, которые удерживают груз весом G = 20 Н в равновесии (рис. 6, а).
Решение. Графическое (рис. 6, б): из точки О на плоскости рисунка строим в выбранном масштабе вектор силы G. Из точки О проводим прямые, параллельные нитям ОМ и ON. Затем из конца вектора G проводим прямые KL и КЕ, чтобы получился параллелограмм, у которого стороны OL и ОЕ соответствуют в данном масштабе искомым силам.
Графоаналитическое (рис. 6, б): Так как известны все углы в треугольнике ОЕК, а также модуль силы G, можно использовать теорему синусов для определения модулей сил F1 и F2:

где 


Задача 3. Фонарь весом 80 Н подвешен на кронштейне ABC, укрепленном на вертикальной стене (рис. 7). Определить усилия, возникшие в горизонтальном стержне СВ и наклонной тяге АВ после подвески фонаря, если СВ = 1 м и АВ = 1,2 м. Соединения в точках А, В и С кронштейна – шарнирные.
Решим задачу графоаналитическим методом по правилу параллелограмма.
1. Используя рис. 7, на котором изображен кронштейн, строим параллелограмм сил. Через произвольную точку а (рис. 29) проводим прямые A1A2 и С1С2, параллельные соответственно тяге АВ и стержню СВ (рис. 7).
Из той же точки а откладываем вертикально вниз отрезок ab, который изображает силу 

2. Теперь имеются две геометрические фигуры – треугольник ABC (см. рис. 7), изображающий заданный кронштейн, и силовой параллелограмм (рис. 8).
Геометрически D ABC (рис. 7) и D adb, или, что все равно, D abc
(рис. 8), подобны между собой.
Используя свойство подобных треугольников (замечаем, что db = ac = Nc), получаем

3. Решая получившиеся пропорции, находим


Неизвестную в кронштейне длину АС найдем по теореме Пифагора (из условия задачи ясно, что угол АСВ – прямой)

Подставляя в выражения для NА и Nc исходные данные, получаем


Задача 4. При помощи двух нерастяжимых нитей АС и ВС удерживается груз, вес которого 12 Н. Положение нитей и груза показано на рис. 9. Определить натяжения нитей.
Решим задачу графоаналитическим методом по правилу треугольника с использованием тригонометрических соотношений.
1. Прежде всего необходимо силу G = =12 Н разложить на две составляющие, линии действия которых совпадают с направлениями линий АС и ВС.
2. Изобразим силу 
3. Если в треугольнике CKL известны углы a, b и g, то задачу легко решить по теореме синусов:

4. Из построения силового треугольника следует, что
(для наглядности положение нитей относительно вектора G показано на рис. 10 штриховой линией). А так как треугольники D АСЕ и D BCD – прямоугольные, то из D ACE
Угол g легко найдем как дополнение к Ð 180°:

5. И теперь, зная углы a, b и g, из уравнения (1)


Таким образом, нить CA растягивается усилием, равным 6,25 Н, а нить СВ – усилием 10,75 Н.
Видео:Вычитание векторов. 9 класс.Скачать

§ 3. Сложение плоской системы сходящихся сил.
Силовой многоугольник
Равнодействующую плоскость системы сходящихся сил можно найти графически с помощью построения силового многоугольника.
Пусть дана система сил F1, F2, F3, F4 (рис. 11, a). Выберем на плоскости чертежа произвольную точку O (рис. 11, б). Из нее проводим в выбранном масштабе вектор, равный по модулю и параллельный силе f1. Из конца этого вектора проводим вектор, равный силе F2. Из конца вектора силы F2 строим вектор, равный и параллельный силе F3, и т. д. Соединив точку О с концом последнего вектора, получим замыкающую сторону многоугольника ON, которая в данном масштабе представляет собой искомую равнодействующую системы – R. Действительно, диагональ силового многоугольника OL равна вектору R1, который является геометрической суммой векторов F1 и F2: R1= F1+ F2 . Вторая диагональ ОМ равна R2= R1+ F3= F1+ F2+ F3. Очевидно, что замыкающая сторона R = R2 + R4 = F1 + F2 + F3 + F4 есть равнодействующая системы, равная геометрической сумме всех заданных сил. Точка приложения равнодействующей совпадает с точкой А.
Модуль и направление равнодействующей не изменятся, если изменить порядок, в котором откладываются векторы сил при построении силового многоугольника.
Следствие. Если система сил является уравновешенной, то равнодействующая системы равна нулю (R = 0). В этом случае силовой многоугольник замкнут, т. е. конец последнего вектора должен совпадать с началом первого.
Замкнутость силового многоугольника является геометрическим условием равновесия плоской системы сходящихся сил. Это условие используют при решении задач на равновесие.
Задача 5. Шар весом G = 20 Н (рис. 12, а) подвешен к вертикальной стене при помощи нити СВ. Определить натяжение нити и силу давления шара на стену, если угол между стеной и нитью a = 30°.
1. Рассмотрим равновесие шара под действием трех сил: силы тяжести G, реакции нити RC и реакции стены RA. Линии действия всех сил пересекаются в центре шара 0.
2. Строим замкнутый силовой треугольник, начиная с известного вектора G (рис. 12, б). Модули неизвестных сил RA и RC, равные соответственно давлению шара на стену и натяжению нити, определим из полученного треугольника:


Задача 6. Определить равнодействующую четырех сил: P1=18 Н, Р2 = 10 Н, Р3 = 6 Н и Р4 = 8 Н, приложенных к одной точке А и направленных, как показано на рис. 13.
Решение – методом проекций на координатные оси.
1. Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами и 
2. Находим проекции данных сил на ось х (рис. 13,б):
3. Находим проекции данных сил на ось у (рис. 13,в):
4. Находим проекции искомой равнодействующей на оси х и у:
Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор 
5. Находим модуль равнодействующей:

6. Находим угол j, определяющий направление R относительно оси у (см. рис. 13, а):
и, следовательно, 
Для определения угла j использован D ABC (см. рис. 13, г), в котором 
Угол j можно найти при помощи синуса:
Таким образом, равнодействующая четырех заданных сил равна 26,7 Н, направлена под углом 40°30′ к положительному направлению оси у и под углом 90° + 40°30′ = 130°30′ к положительному направлению оси х.
Задача 7. К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: Р1 = 40 H, Р2 = 25 H, P3 = 25 H и P4 = 20 H, направленные, как показано на рис. 14, а (сила Р2 горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.
Решение – методом проекций.
1. Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.
2. Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 14, б) и совместим оси проекций с силами 

3. Найдем проекции заданных сил на ось х:
4. Найдем проекции заданных сил на ось у:
5. Найдем проекции равнодействующей на оси х и у:
6. Найдем модуль равнодействующей:

Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.
Таким образом, четыре заданные силы натягивают веревку равнодействующей силой R, приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.
Другой конец веревки (точка А, рис. 14, а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.
На рис. 14, в показаны равнодействующая R и уравновешивающая 
Задача 8. На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами Р1 = 4 кH и Р2 = 0,8 кH, как показано на рис. 15, а. Под каким углом к этому стержню следует присоединить второй стержень ВС, чтобы стержень АВ растягивался силой РА = 2 кН. Какое усилие при этом будет испытывать стержень ВС?
Соединения стержней между собой и с опорами шарнирные.
Решение – методом проекций.
1. На точку В действуют три силы: – вертикально вниз, 
2. Оси проекций совместим с силами и 
3. Обе проекции получаются отрицательными. Значит, равнодействующая расположится так, как показано штриховым на рис. 15, б, и положение стержня ВС определится углом 
4. Определим значение угла a из треугольника, образуемого и его проекциями (рис. 15, в):

5. Стержень ВС необходимо установить под 

Описанное положение стержня показано на рис. 15, г.
Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кН.
Задача 9. Определить равнодействующую пяти сил:
Р1 = 52 Н, Р2 = 70 Н, Р3 = 69 Н, Р4 = 77 Н, Р5 = 70 Н, действующих на точку А, как показано на рис. 16, а.
Решение – методом проекций.
1. Так как силы и направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы 

2. Найдем проекцию равнодействующей на ось х:
3. Найдем проекцию равнодействующей на ось у:
4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.
Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.
Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

§ 4. Проекция силы на ось.
Проекция силы на две взаимно-перпендикулярные оси координат
Кроме рассмотренных выше графического и графоаналитического методов решения задач, в статике широко распространен аналитический метод их решения, или метод проекций.
Проекцией силы на ось (рис. 17) является отрезок оси, заключенный между проекциями на эту ось начала и конца вектора силы. Проекцию обычно обозначают той же буквой, что и силу, но с индексом. Например, Fx – проекция силы F на ось х.
Проекция силы на ось есть величина скалярная. Она может быть положительной, отрицательной или равной нулю в зависимости от величины угла a между направлением силы и положительным направлением оси. Из прямоугольного треугольника ABC следует, что Fx = F сos a, т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
Если угол a острый, то проекция положительна (рис. 17), если угол a – тупой, то проекция отрицательна (рис. 18, а):
Нетрудно убедиться, что проекция силы на ось будет равна нулю, если a = 90° или 270° (рис. 18, б), и равна модулю силы, если a = 0 или a = 180° (рис. 18, в).
Модуль и направление силы можно определить по ее проекциям на две взаимно перпендикулярные оси (рис. 18, в):
Из треугольника ABC, поскольку АС = Fx и ВС = Fy, следует, что модуль силы F равен

Направление силы определяют косинусы углов (рис. 19):


Задача 10. В точке В кронштейна ABC (рис. 20, а) подвешен груз М весом 8 кН. Определить реакции стержней кронштейна, если углы кронштейна a = 110°, b = 30° и крепления в точках А, В и С шарнирные.
Решение – методом проекций при помощи уравнений равновесия.
1. Так как три силы 
2. Выберем оси координат так, чтобы одна из осей совпадала с линией действия одной из неизвестных сил (рис. 21), и составим два уравнения равновесия:



Задача 11. К шарниру В кронштейна ABC прикреплена веревка, перекинутая через блок, к другому концу которой прикреплен груз весом G = l,5 кН (рис. 22). Определить усилия в стержнях АВ и СВ кронштейна, если крепления в точках А и С шарнирные, a = 35° и b = 100°.
Решим задачу методом проекций.
1. Изобразив шарнир В вместе с действующими на него силами 


2. Из уравнения (2)

а из уравнения (1)
Итак, реакции стержней (их действия на шарнирный болт В) равны NA = 2,57 кН и NС = l,85 кН. Точно с такими же усилиями действует шарнирный болт на стержни. Стержень АВ растянут силой 2,57 кН, а стержень СВ сжат силой 1,85 кН.
Видео:Сложение векторов. 9 класс.Скачать

Разложение силы на сходящиеся составляющие
Разложение силы на сходящиеся составляющие
Разложить силу на две или несколько составляющих—значит найти такую систему двух или нескольких сил, равнодействующая которых была бы равна данной силе. При разложении силы, в частности, на сходящиеся составляющие, необходимо, чтобы она по модулю и но направлению изображалась замыкающей стороной силового многоугольника, построенного на составляющих силах как на сторонах.
Так как можно построить бесчисленное множество многоугольников, у которых замыкающий вектор равнялся бы данном силе, то для определенности решения задачи должны быть известны дополнительные условия.
Рассмотрим два, наиболее часто встречающихся, случая.
- Заданную силу
требуется разложить на две сходящиеся силы, заданные направления
и
которых (рис. 19) лежат в одной плоскости с этой силой.
Для решения задачи из конца 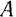
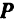
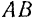
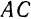
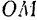
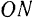
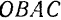
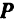
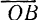
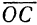
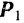
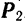
Так как сумма непараллельных сторон параллелограмма всегда больше каждой из его диагоналей, то сумма модулей двух сходящихся составляющих, на которые мы разлагаем заданную силу, всегда больше модуля этой силы.
Чем больше угол между направлениями составляющих сил, тем больше и их модули. При достаточно большом угле между составляющими модуль каждой из них может быть и больше модуля разлагаемой силы.
- Заданную силу
требуется разложить на три сходящиеся составляющие, заданные линии действия
и
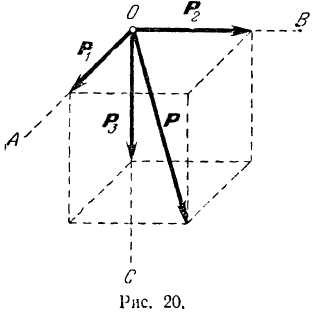
которых не лежат в одной плоскости (рис. 20).
Для решения этой задачи нужно построить параллелепипед, диагональ которого должна изображать по модулю и по направлению заданную силу. Совпадающие с заданными направлениями составляющих ребра этого параллелепипеда будут изображать, в масштабе, принятом для силы 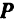
Пример задачи:
Кран 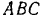
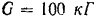
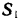
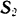
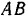
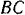
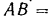
Решение:
Разлагаем силу 
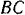
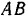
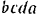
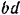

Длины сторон 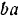
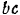

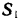
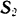
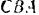
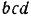
Если учесть направление сил 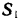
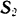
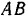
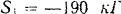
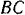
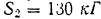
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Разложение вектора по базису. 9 класс.Скачать

Системы сил
Видео:№764. Пользуясь правилом многоугольника, упростите выражения: а) (АВ + ВС -МС)Скачать

Плоская система сходящихся сил
На тело одновременно могут воздействовать несколько сил. Как уже говорилось, совокупность нескольких сил, приложенных к телу, называется системой сил. Силы могут лежать в одной плоскости, в таком случае они образуют плоскую систему сил, и в разных плоскостях, соответственно, составляя объемную систему сил.
При решении задач может возникнуть необходимость замены исходной системы сил другой, упрощающей решение. Подобная замена разрешена, когда системы сил эквивалентны.
Эквивалентные системы сил — это системы различающихся сил, но оказывающие одинаковое механическое воздействие на тело.
Отсюда следует вывод, что когда две системы сил эквивалентны третьей системе, они эквивалентны и между собой.
Различают: системы сходящихся сил и системы произвольно расположенных сил. Далее рассматриваем плоскую систему сходящихся сил (рис. 2.1а).
Система сходящихся сил — это система сил, все силы которой или все линии их действия, сходятся в одной точке.
Когда хотя бы одна сила или линия ее действия не пересекается в точке схождения остальных сил, такая система называется системой произвольно расположенных сил. Так, на рис. 2.16 векторы сил и линии их действия не пересекаются в одной точке, соответственно, имеет место система произвольно расположенных сил.
Для сложения сил в соответствии с четвертой аксиомой статики необходимо, чтобы силы сходились в одной точке. Следовательно, систему сходящихся сил можно упростить, последовательно складывая составляющие ее силы. Сложение сил можно вести графически, складывая векторы сил, и аналитически, воспользовавшись для сложения формулой (1.5).
Рис. 2.1. Плоские системы сил: а) плоская система сходящихся сил; б) плоская система произвольно расположенных сил:
1 — абсолютно твердое тело
Систему сходящихся сил всегда можно заменить одной силой, равнодействующей R (рис. 2.2а, б), она эквивалентна по своему механическому воздействию на тело исходной системе сил.
Рис. 2.2. Эквивалентные системы сил: а) исходная система сил; б) равнодействующая сил системы
Понять состояние тела, например, находится оно в равновесии или не находится, если на него действует много разнонаправленных сил, можно только упростив систему сил. Если равнодействующая системы сил, приложенных к телу, не равна нулю, это значит, что тело не находится в равновесии. Равнодействующая будет постоянно воздействовать на тело, и оно будет ускоренно двигаться в направлении воздействия.
Уравновешенная система сил эквивалентна системе сил равной нулю, иначе говоря, сумма всех сил в уравновешенной системе равна нулю, соответственно и равнодействующая равна нулю.
Рассмотрим плоскую систему сил, состоящую из трех сил, сходящихся в точке А (рис. 2.3а). В соответствии с третьей аксиомой статики силы можно переносить по линиям их действия. Перемещаем все силы так, чтобы они исходили из точки А (рис. 2.3б). Переносим силу F по линии 1-1, силу Fi по линии 2-2, силу F3 по линии 3-3. Затем можно последовательно выполнять их сложение, используя правило параллелограмма или правило треугольника. Складываем сначала силы F и Fi и получаем их равнодействующую /?(i-2), затем равнодействующую R( 1-2) суммируем с силой F3 и получаем общую равнодействующую всей системы сходящихся сил R = F + F2 + F3 (рис. 2.3в).
Нахождение равнодействующей можно упростить, выполняя построение силового многоугольника. Последовательно из конца вектора предшествующей силы откладываем вектор следующей силы, замыкающий вектор, проведенный из начала первой силы (точки А) к концу последней силы (точке С), и будет равнодействующей всей системы сил R (рис. 2.3г). Иными словами, равнодействующая замкнет многоугольник сил. Вектор равнодействующей исходит из точки начала построения и направлен к концу последней силы силового многоугольника.
В статике силы прикладывают либо к абсолютно твердым телам, либо к материальным точкам. На рисунке 2.3 равнодействующая приложена к материальной точке А.
Рис. 2.3. Сложение сил: а) исходная система сил; б) перенос сил в точку схождения линий их действия; в) последовательное сложение сил по правилу параллелограмма; г) сложение сил путем построения силового многоугольника
Строя силовой многоугольник, можно суммировать любое количество сходящихся сил. Длины векторов складываемых сил должны соответствовать принятому масштабу и при их переносе следует следить за тем, чтобы они переносились параллельно своим исходным направлениям. Зная масштаб сил и измерив длину вектора равнодействующей, можно определить значение модуля равнодействующей.
Если последняя из слагаемых сил силового многоугольника заканчивается в начальной точке построения, равнодействующая равна нулю, и, следовательно, такая система сил находится в равновесии.
Если ставится условие, что система сил должна находиться в равновесии, но это условие не выполняется, необходимо в систему сил добавить уравновешивающую силу, она по модулю должна быть равна равнодействующей (FypaBH = R) и направлена в противоположную сторону — из точки С в точку А (рис. 2.4). Заменив равнодействующую уравновешивающей силой, мы обеспечиваем равновесие всей системы сил. При этом силовой многоугольник замкнется.
Рис. 2.4. Для равновесия системы сил следует заменить равнодействующую уравновешивающей силой
Условие равновесия системы сходящихся сил записывается как равенство нулю всех сил системы:
Пример 2.1. Используя правила построения силового многоугольника, сложить силы, входящие в систему сходящихся сил (рис. 2.5а), и привести систему в состояние равновесия. Сила F = 15 Н, Fi = 9 Н, Ез = 16 Н, Fa = 26 Н. Векторы сил системы на рис. 2.5 изображены в масштабе: 1 мм длины соответствует 1 Н.
Решение. 1. Сохраняя направления линий действия сил и длину векторов сил, строим силовой многоугольник: из конца вектора первой силы проводим вектор второй силы, перенося его параллельно исходному направлению, затем из конца второго вектора откладываем параллельно начальному направлению третий вектор и т.д. Замыкает силовой многоугольник равнодействующая R, которая и является суммой всех сил (рис. 2.5б).
2. Замеряем длину вектора равнодействующей и переводим длину с учетом принятого масштаба в ньютоны.
Рис. 2.5. Сложение сил методом силового многоугольника: а) исходная система сил; б) силовой многоугольник; в) уравновешенная система сил
3. Для обеспечения равновесия системы сил к точке А прикладываем уравновешивающую силу, которую направляем в противоположную от равнодействующей сторону по ее линии действия, принимая их модули равными (рис. 2.5в). Для системы сил, изображенной на рис. 2.5в, выполняется условие равновесия (2.1). Если направление действия равнодействующей принять за
положительное, получим ? Fi = 0; R — FypaBH = 0.
Следует отметить, что от точности построения силового многоугольника зависит точность графического определения модулей равнодействующей и уравновешивающей силы, а также правильное нахождение направления их действия.
Задача 2.1. Сложите силы, входящие в систему сходящихся сил (рис. 2.6). Для сложения используйте правила построения силового многоугольника. Примите масштаб сил: 1 мм — 0,5 Н. Сила F = 8 Н, F2 = 24 Н, F3 = 12 Н.
Задача 2.2. По данным задачи 2.1 определите силу, которая приведет систему, изображенную на рис. 2.6, в равновесие.
Задача 2.3. Постройте силовой многоугольник и определите значение равнодействующей. Система сил изображена на рис.
Рис. 2.7. Система сил, к задаче 2.3
Задача 2.4. Дана сходящаяся система из трех сил F, F2, F3, которая находится в равновесии (рис. 2.8). Модули сил: F = 30 кН, F2 = 20 кН. Определите направление силы F3 и ее модуль (сила условно изображена пунктиром).
Рис. 2.8. Система сил, к задаче 2.4
Задача 2.5. Даны два силовых многоугольника (рис. 2.9). Определите, в каком случае система сходящихся сил находится в равновесии?
📸 Видео
Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Найдите разложение вектора по векторам (базису)Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Вариант №4 - Уровень сложности реального ЕГЭ 2024 | Математика профильСкачать

Урок 11. Решение задач на действия с векторамиСкачать

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Сложение векторов. Практическая часть. 9 класс.Скачать

































































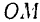 и
и 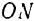 которых (рис. 19) лежат в одной плоскости с этой силой.
которых (рис. 19) лежат в одной плоскости с этой силой.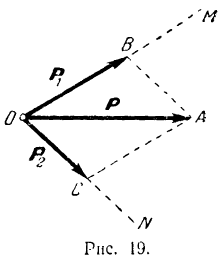
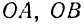 и
и 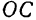 которых не лежат в одной плоскости (рис. 20).
которых не лежат в одной плоскости (рис. 20).