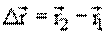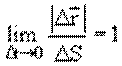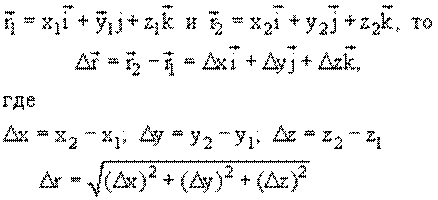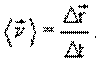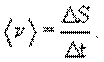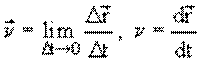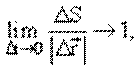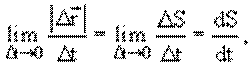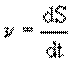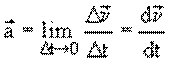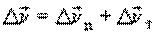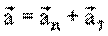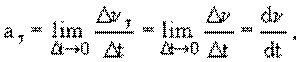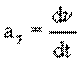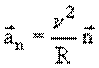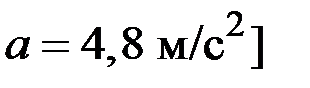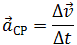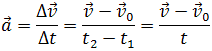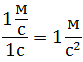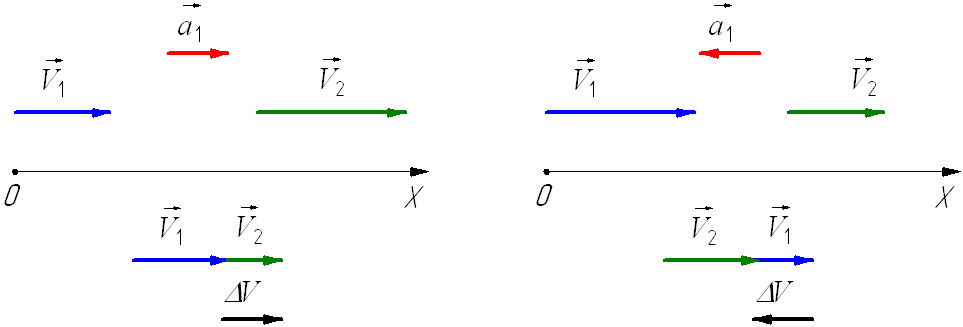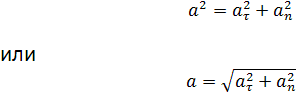Страницы работы
Содержание работы
Вопросы к экзамену по первой части курса «Физика»
1. Кинематика материальной точки. Координатная и векторная формы описания движения. Перемещение, скорость и ускорение материальной точки.
2. Виды движения материальной точки. Прямолинейное (равномерное и равноускоренное) движение. Движение по окружности. Криволинейное движение. Скорость и ускорение (нормальное, тангенциальное) при криволинейном движении.
3. Законы Ньютона. Их взаимосвязь и границы применимости.
4. Закон инерции. Инерциальные системы отсчета. Принцип относительности Галилея.
5. Второй закон Ньютона. Силы: сила тяжести, сила упругости, сила трения. Движение под действием этих сил.
6. Третий закон Ньютона. Импульс. Закон сохранения импульса.
7. Центр масс. Теорема о движении центра масс.
8. Движение в центральном поле сил. Закон всемирного тяготения.
9. Соударение двух тел. Абсолютно упругий и абсолютно неупругий удар.
10. Консервативные силы и потенциальное поле. Работа в потенциальном поле. Кинетическая и потенциальная энергия. Закон сохранения энергии в механике.
11. Момент импульса и момент силы относительно неподвижного начала. Уравнение моментов. Закон сохранения момента импульса.
12. Момент импульса и момент сил относительно неподвижной оси. Уравнение динамики вращательного движения относительно неподвижной оси.
13. Момент инерции. Теорема Штейнера. Кинетическая энергия вращающегося твердого тела.
14. Гармонические колебания и их характеристики. Комплексная форма представления гармонических колебаний. Сложение гармонических колебаний одинаковых и близких частот. Биения.
15. Гармонический осциллятор. Уравнение динамики гармонических колебаний. Примеры гармонических осцилляторов: пружинный, физический и математический маятники.
16. Затухающие колебания. Время релаксации. Коэффициент затухания. Логарифмический декремент затухания.
17. Вынужденные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс.
18. Волны. Продольные и поперечные волны. Одномерное волновое уравнение. Интерференция волн. Стоячие волны.
19. Состояние равновесия. Макроскопические параметры. Уравнения состояния.
20. Законы идеальных газов: закон Бойля-Мариотта, закон Гей-Люссака, закон Авогадро, закон Дальтона.
21. Уравнение состояния и внутренняя энергия идеального газа. Степени свободы. Теорема о равнораспределении энергии по степеням свободы.
22. Давление газа с точки зрения молекулярно-кинетической теории. Молекулярно-кинетический смысл температуры.
23. Функция распределения молекул по скоростям. Распределение Максвелла.
24. Барометрическая формула. Распределение Больцмана.
25. Изопроцессы. Изопроцессы идеального газа.
26. Теплоемкость. Теплоемкость идеальных газов. Уравнение Майера.
27. Первое начало термодинамики. Макроскопическая работа, количество тепла.
28. Второе начало термодинамики. Равенство Клаузиуса. Энтропия.
29. Явления переноса. Распределение молекул по длинам свободного пробега. Средняя длина свободного пробега.
30. Уравнение Ван-дер-Ваальса. Критическое состояние вещества.
31. Фазы. Условия равновесия фаз. Уравнение Клапейрона-Клаузиуса.
Ответы
1 Кинематика материальной точки- изучает законы перемещения материальной точки в зависимости от времени без учета причин, вызывающих это перемещение. Материальная точка- тело, размерами которого в условиях данной задачи можно пренебречь.
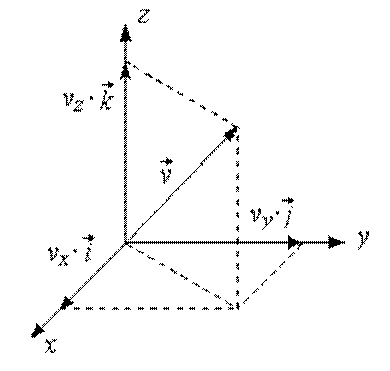
Мгновенное положение материальной точки (Р) в пространстве можно описать при помощи радиуса-вектора 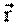
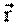

где (x, y, z) – проекции вектора на координатные оси (координаты точки), 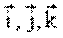
В векторной форме радиус-вектор записывается:
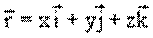
длина вектора (модуль вектора):
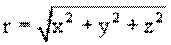
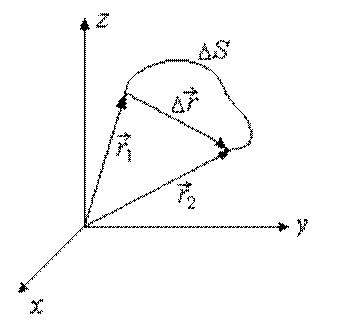
При движении материальной точки конец ее радиуса-вектора описывает в пространстве некоторую линию (годограф), называемую траекторией. Форма траектории определяет характер движения – прямолинейное или криволинейное. Длина траектории называется длиной пути (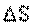
Разность радиусов-векторов, определяющих два положения материальной точки в моменты времени t1 и t2, называется вектором перемещения 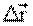
При прямолинейном движении модуль вектора перемещения 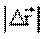
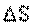
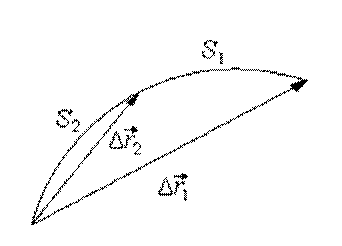
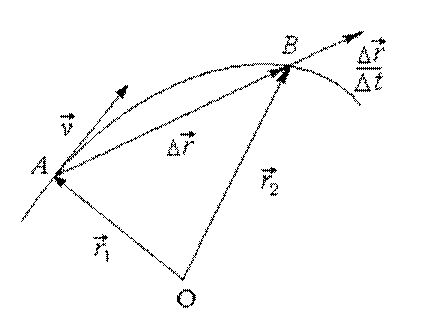
В общем случае криволинейного движения это равенство возможно лишь для бесконечно малого отрезка времени (рис. 1.3):
Запишем вектор перемещения 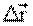
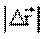
Пусть материальная точка движется по криволинейной траектории из точки А, положение которой задается радиусом-вектором 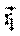
Через некоторое время 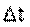
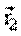
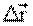
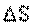
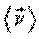
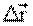
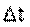
Средней путевой скоростью называется отношение:
Уменьшим время наблюдения, при этом перемещение 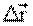
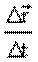
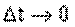
Единица измерения скорости – [м/с].
Вектор скорости – первая производная радиуса–вектора по времени. Модуль вектора скорости – первая производная пути по времени. Так как
Запишем вектор скорости в координатной форме
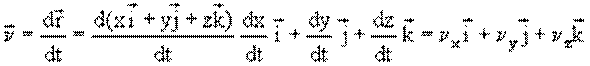
где 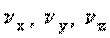
(рис. 1.5).
Модуль вектора скорости равен:
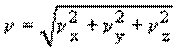
В случае, если тело за сколь угодно малые равные промежутки времени 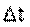
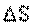
Так, движение точки по окружности с постоянной по величине скоростью является равномерным, но криволинейным.
1. 3. Ускорение. Тангенциальное, нормальное и полное ускорение
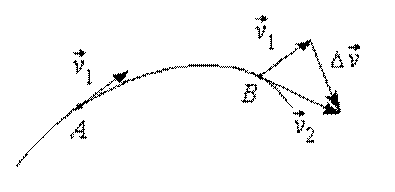
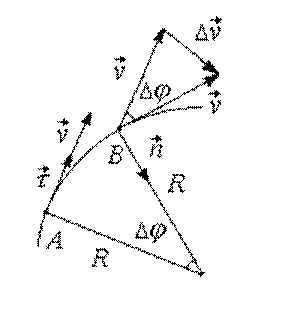
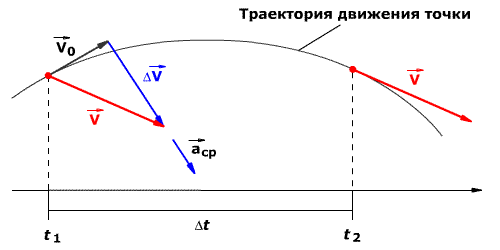
В общем случае, при движении материальной точки по криволинейной траектории вектор скорости может меняться по величине и направлению. Пусть за малый промежуток времени 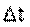
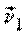
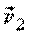
Перенесем вектор скорости 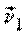
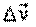
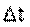
Векторная величина, равная пределу, к которому стремится отношение 
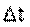
Вектор ускорения равен первой производной вектора скорости по времени:
Как всякий вектор, ускорение можно представить в виде суммы проекций на оси (x, y, z):
Модуль вектора ускорения
Единица измерения ускорения – [м/c 2 ].
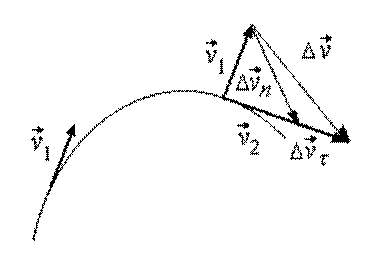
Вектор ускорения 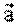
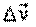
Пусть за время 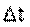
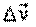
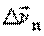
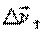
В этом случае вектор ускорения 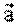
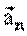
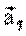
где 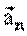
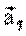
Тангенциальное ускорение удобно рассмотреть на примере неравномерного прямолинейного движения. При этом скорость изменяется только по величине 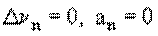
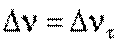
В векторной форме 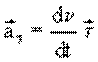
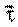
Нормальное ускорение удобно рассмотреть на примере равномерного движения по окружности. При этом 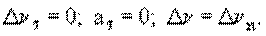
Перенесем вектор скорости из точки А в точку В методом параллельного переноса (рис. 1.8).
Если время перемещения точки из А в В мало, то малый угол поворота радиуса-вектора точки может быть записан следующим образом:
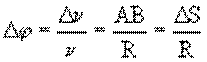
где АВ – длина дуги окружности радиуса R, 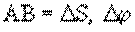
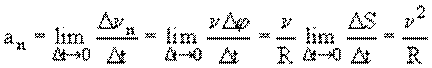
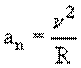
В векторной форме:
где 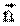
Таким образом, вектор полного ускорения материальной точки равен
Видео:Прямолинейное и криволинейное движение | Физика 9 класс #17 | ИнфоурокСкачать

Статистическая физика и термодинамика
Кинематика поступательного и вращательного движения
Тестовые задания
1.1. Вектор скорости …
1) является количественной мерой изменения положения материальной точки
2) всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело
3) всегда направлен вдоль вектора перемещения
4) всегда направлен вдоль вектора ускорения
5) направлен перпендикулярно радиус-вектору материальной точки
1.2.Вектор средней скорости материальной точки совпадает по направлению с …
1) касательной к траектории
2) радиус-вектором, определяющим положение точки
3) вектором полного ускорения
4) вектором нормального ускорения
5) вектором перемещения
1.3.Материальная точка движется равномерно по окружности радиусом R с периодом Т. Модуль вектора средней скорости за четверть оборота равен …
1) 



1.4.Материальная точка движется равномерно по окружности со скоростью 
1) 0 2) 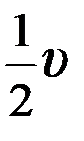


1.5.Материальная точка движется равномерно по окружности радиусом 

1) 



| –2 |
 , м/с , м/с |
 , с , с |
| –1 |
| –3 |
1.6. Зависимость проекции скорости движения материальной точки по прямой от времени дана на рисунке. Перемещение материальной точки за первые 5 с движения равно … м.
1) 6 2) 5,5 3) 7 4) 5 5) 8
| 1 2 3 4 5 t, c |
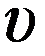 , м/с –2 , м/с –2 |
1.7.Зависимость скорости движения материальной точки по прямой от времени дана на рисунке. Среднее значение модуля скорости движения материальной точки в интервале времени 0-5 с равно … м/с.
1) 1,5 2) 0,25 3) 2,5 4) 0,2 5) 1,4
1.8. Поезд движется на подъеме со скоростью 

1) 



1.9. Радиус-вектор частицы определяется выражением 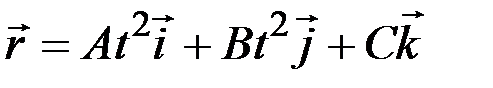
1) 15 2) 20 3) 21 4) 35 5) 42
1.10.Материальная точка движется так, что радиус-вектор меняется со временем по закону 

1)
2)
3)
4)
5)
1.11. Радиус-вектор точки изменяется со временем по закону 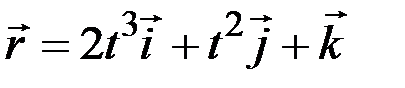
1) 12,2 2) 24,1 3) 24,3 4) 26 5) 29
| y |
| х |
| А |
1.12. Радиус-вектор частицы изменяется со временем по закону 
1) 1 2) 2 3) 3 4) 4 5) 5
1.13.Из точек А и В навстречу друг другу движутся два тела. Уравнения движения тел имеют вид: 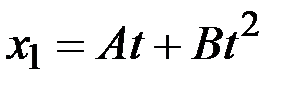
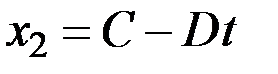
1) 5 2) 11,2 3) 10 4) 7,8 5) 5,6
1.14. Две материальные точки движутся согласно уравнениям: 

1) 0,94 2) 0,54 3) 0,65 4) 0,74 5) 0,82
1.15. Зависимость пройденного телом пути от времени дается уравнением 
1) 11 2) 5 3) 5,5 4) 6 5) 7
1.16.Две материальные точки движутся согласно уравнениям: 

1) 1,00 2) 0,235 3) 0,542 4) 0,845 5) 0,9
1.17. Тело начинает двигаться из состояния покоя с постоянным ускорением 2 см/с 2 . За третью секунду своего движения оно пройдет путь … см.
1) 9 2) 2 3) 3 4) 4 5) 5
1.18.Материальная точка начинает двигаться вдоль прямой так, что её ускорение прямо пропорционально квадрату времени ( 
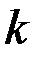
1) от времени не зависит
2) 


1.19. Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 100 м из него выбрасывается вверх предмет со скоростью 2 м/с относительно вертолета. Предмет упадет на землю через … с.
1) 4,5 2) 5,3 3) 5,6 4) 5,8 5) 6,0
1.20.Из одной и той же точки с интервалом 2 с брошены вертикально вверх два шарика с одинаковыми скоростями 30 м/с. Они столкнутся после броска первого шарика через … с.
1) 1 2) 2 3) 3 4) 4 5) 5
1.21. Камень падает с высоты 
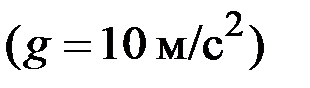
1) 1050 2) 150 3) 300 4) 450 5) 600
1.22. Мяч брошен под углом 60º к горизонту с начальной скоростью 10 м/с. Скорость мяча через 0,2 с после броска равна … м/с.
1) 2 2) 8,4 3) 8,7 4) 9,2 5) 12,5
1.23. Камень брошен с башни в горизонтальном направлении. Через 3 с вектор скорости камня составил угол в 45º с горизонтом. Начальная скорость камня равна … в м/с.
1) 10 2) 15 3) 3 4) 20 5) 30
| ● |
| α |
| ● |
| ● |
| ● |
| ● |
| А |
| В |
| С |
| Е |
| D |
 |
1.24.Камень бросили под углом к горизонту со скоростью 
1) увеличиваются; увеличиваются
2) уменьшаются; уменьшаются
3) увеличиваются; уменьшаются
4) уменьшаются; увеличиваются
5) уменьшаются; не изменяются
1.25.Тело брошено под углом 

1) 
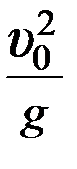


1.26.Тело брошено под углом 

1) 0 2) 
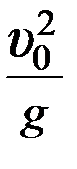

1.27.Скорость камня в точке его падения составила с горизонтом угол 
1) 



| α |
 |
| S |
1.28.Два тела брошены под одним и тем же углом к горизонту с начальными скоростями 
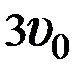
1) 
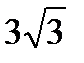
| аτ |
| t |
1.29.Тангенциальное ускорение точки меняется согласно графику. Такому движению может соответствовать зависимость скорости от времени …
| а б в г |
| υ |
| t |
| υ |
| t |
| υ |
| t |
| υ |
| t |
1) а 2) б 3) в 4) г
1.30. Материальная точка движется замедленно по криволинейной траектории. Направление скорости показано на рисунке. Направление векторов полного и тангенциального ускорений правильно изображено на рисунках соответственно …
 |
| а |
 |
>
 |
| б |
 |
>
 |
| в |
 |
>
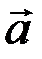 |
| г |
 |
>
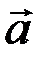 |
| д |
 |
>
1) в; г 2) а; б 3) б; а 4) а; в 5) г; а
1.31. Материальная точка М движется по окружности со скоростью 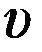

 |
| t |
| t3 |
| t2 |
| t1 |
| t |
| M |
| τ |
| ● |
| О |
| Рис. 1 |
| Рис. 2 |
1) 5 2) 1 3) 2 4) 3 5) 4
1.32.При равнозамедленном движении материальной 
1) 1 2) 2 3) 3 4) 4 5) равен нулю
 |
| ● |
 |
| ● |
| ● |
| ● |
| ● |
| А |
| В |
| С |
| Е |
| D |
 |
1.33.Камень бросили под углом к горизонту со скоростью 
1) максимален в т. А и Е
2) максимален в т. В и D
3) во всех точках одинаков
4) максимален в т. С
| ● |
| ● |
| А |
| В |
1.34. Тело движется с постоянным нормальным ускорением по траектории, изображенной на рисунке. Для величины скорости тела в т. А 

1) 
3) 
5)
h fKzkYxUlo6AdYPeGkbCeeUdQWOfjm77Lsw6yCZruEZd6QrAr7NrwMzFtx5meNBg5GSUZSafe3lYa vQVlPVXvqpmqoMiFjIx+yBgPQ60HkpL4sNY0yRmWzoKypkr7EAnKJVPZI6akk8rYtH6MIOPmZ+UX z7XkellZUJ4oVi8w87rE9RYCMu2y9KCJl7Vhek6nKfgciuWUgLo8gF/y0lpQ/rPqXTUEWSoCRCBF RM71GL8A6dcmmGLTf5vvr+l7bArWynwuyxO+jglNmbQWlCmxPqWXHCEgozvyMj0jtSJOi5WneEab tADNCNQ0irUdydpG+nWJEC9CATeTTkkSmWsqIGs2yysyBJ0EDciAo7xEFmxSIbnpJShQdklLNFOt gUqZ9BYUmN7jIlSK2yK5yCJoQILizorkJKugIrlRUCkaBZWCmc3+AdOizh2wLk2pAAAAAElFTkSu QmCCUEsBAi0AFAAGAAgAAAAhALGCZ7YKAQAAEwIAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50 X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAA7AQAA X3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA/Y4FPRcCAABjBAAADgAAAAAAAAAAAAAAAAA6AgAA ZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAqiYOvrwAAAAhAQAAGQAAAAAAAAAAAAAAAAB9 BAAAZHJzL19yZWxzL2Uyb0RvYy54bWwucmVsc1BLAQItABQABgAIAAAAIQDitnMz4AAAAAkBAAAP AAAAAAAAAAAAAAAAAHAFAABkcnMvZG93bnJldi54bWxQSwECLQAKAAAAAAAAACEAr1K8f8wFAADM BQAAFAAAAAAAAAAAAAAAAAB9BgAAZHJzL21lZGlhL2ltYWdlMS5wbmdQSwUGAAAAAAYABgB8AQAA ewwAAAAA «> 
1) не изменяется 2) увеличивается 3) уменьшается
| ● |
| M |
1.36.Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелками. При этом величина полного ускорения …
1) уменьшается 2) не изменяется 3) увеличивается
1.37.Материальная точка движется равномерно по окружности радиусом 

1) 
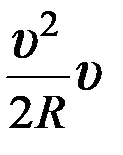

1.38.Точка движется по окружности радиусом R = 2 м согласно уравнению l = Аt 3 , А = 2 м/с 3 , l – длина дуги от начала движения. Нормальное ускорение равно тангенциальному в момент времени … с.
1) 2 2) 0,874 3) 0,760 4) 0,667 5) 0,3
1.39.Две материальные точки начинают двигаться по окружности из одной начальной точки: первая с ускорением 0,10 рад/с 2 , вторая – с ускорением 0,15 рад/с 2 . Впервые после начала движения они встретятся через … с.
1) 0,2 2) 31,7 3) 47,5 4) 15,8 5) 75,0
1.40. Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением 
1) 1 2) 2 3) 2,5 4) 3 5) 4


1) 5 2) 4 3) 1 4) 3 5) 2
1.42. Материальная точка движется равнозамедленно по окружности, лежащей в вертикальной плоскости, по часовой стрелке. Вектора угловой скорости и углового ускорения направлены соответственно …
2) по касательной к траектории; к нам
3) к нам; по радиусу от центра
4) от нас; по касательной к траектории
1.43.Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости ωZ(t) так, как показано на рисунке. Вектор углового ускорения 
| t3 |
| t4 |
| Z |
| ωZ |
| t1 |
| t |
| t2 |
1.44. Закон изменения угла поворота φ со временем имеет вид 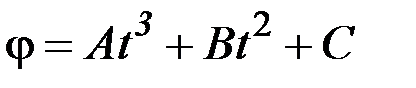

1) 19; 56 2) 56; 46 3) 88; 56 4) 86; 19 5) 76; 29
1.45. Точка вращается по окружности радиусом 


А)
Б)
В)
Г)
Д)
1) А; Г 2) В; А 3) Д; Г 4) Д; Б 5) А; Б
1.46.Тело вращается вокруг неподвижной оси по закону 
1) 3,20 2) 1,65 3) 1,60 4) 0,40 5) 0
1.47.На вал радиусом 10 см намотана нить, к концу которой привязана гиря. Опускаясь равноускоренно, гиря прошла расстояние 5 см за 2 с. Тангенциальное ускорение точки, лежащей на поверхности вала, равно … см/с 2 .
1) 25 2) 0,5 3) 5 4) 2,5 5) 3,5
1.48.Частица из состояния покоя начала двигаться по дуге окружности радиусом R = 1 м с постоянным угловым ускорением ε = 2 рад/с 2 . Отношение нормального ускорения к тангенциальному через одну секунду равно …
1) 8 2) 2 3) 1 4) 4 5) 3
1.49. Материальная точка вращается в горизонтальной плоскости относительно неподвижной оси с угловым ускорением ε = А t 2 , где А = 2 рад/с 4 . При t = 0 ω0 = 0. Закон изменения угловой скорости имеет вид …
1) ω = 3/2 t 3 2) ω = 2t 3 3) ω = 2/3 t 3 4) ω = 4t 5) ω = 4t 3
1.50.Закон изменения угловой скорости материальной точки имеет вид 
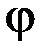
1) 6 2) 40 3) 65 4) 80 5) 125
1.51.Маховик вращается равнозамедленно с угловым ускорением ε = 2 рад/с 2 . Угол поворота φ при изменении частоты вращения от n1 = 240 мин –1 до n2 = 90 мин –1 равен … рад.
1) 4 2) 1479 3) 136 4) 22 5) 5
1.52. Тело движется по окружности так, что его угловая скорость изменяется по закону 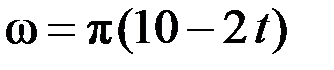
1) 4 2) 5 3) 6,28 4) 10 5) 12,5
1.53.Если 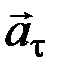

А) 
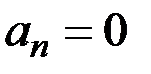



Г) 
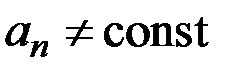

1) В; Д; А 2) Д; В; Б 3) В; Г; А 4) Д; Б; А 5) Г; В; Б
Задачи
1.54.По гладкой наклонной доске пустили катиться снизу вверх маленький брусок. На расстоянии l = 30 см брусок побывал дважды: через t1 = 1 с и через t2 = 2 c после начала движения. Определите начальную скорость бруска 
1.55.Движение точки по кривой задано уравнениями 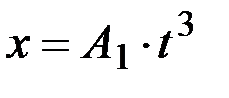






1.56.С башни брошен камень в горизонтальном направлении с начальной скоростью 40 м/с. Вычислить скорость камня через 3 с после начала движения. Какой угол образует вектор скорости камня с плоскостью горизонта в этот момент? 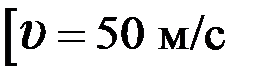
1.57.Снаряд вылетел со скоростью 30 м/с под углом 60º к горизонту. Чему равен радиус кривизны траектории снаряда через 2 с после выстрела?
1.58.Мяч брошен со скоростью 


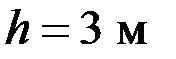


1.59.Под каким углом к горизонту надо бросить тело, чтобы центр кривизны его траектории в вершине находился на земле?
1.60.Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением S = At 3 , где А = 0,1 см/с 3 . Найдите нормальное (аn) и тангенциальное (аτ) ускорения точки в момент, когда линейная скорость точки 
1.61.Точка движется по окружности радиусом 


1.62.Зависимость угла поворота от времени для точки, лежащей на ободе колеса радиусом R, задается уравнением 


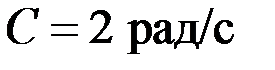

1.63. Диск радиусом 10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 0,5 рад/с 2 . Найдите касательное, нормальное и полное ускорения точек на окружности диска в конце второй секунды после начала вращения.
1.64.Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R = 10 м. Уравнение движения автомобиля 
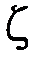
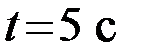
1.65.Диск радиусом R =10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением 

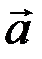

1.66.Материальная точка начинает движение по окружности радиусом 12,5 см с постоянным тангенциальным ускорением 0,5 см/с 2 . Определите момент времени, когда угол между векторами ускорения и скорости равен 45º и путь, пройденный точкой до этого момента.
1.67.Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аτ. Найдите тангенциальное ускорение аτ точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки 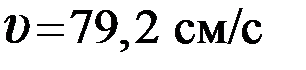
Видео:Модель материальной точки. Радиус вектор | ФизикаСкачать

Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Видео:ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где 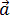
Направление вектора ускорения совпадает с направлением изменения скорости Δ 



В момент времени t1 (см. рис 1.8) тело имеет скорость 




Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ 
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть а направление вектора ускорения совпадает с вектором скорости 
Если скорость тела по модулю уменьшается, то есть то направление вектора ускорения противоположно направлению вектора скорости 
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 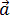
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 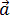
Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
💥 Видео
Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Перемещение | Физика 9 класс #2 | ИнфоурокСкачать

Траектория, материальная точкаСкачать
Материальная точка. Система отсчета | Физика 9 класс #1 | ИнфоурокСкачать

Лекция 3.4 | Перемещение и скорость материальной точки | Александр Чирцов | ЛекториумСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Физика - движение по окружностиСкачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Вращательное движение. 10 класс.Скачать

Задача о полном ускорении при неравномерном движении тела по окружности.Скачать

Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать