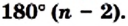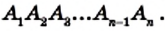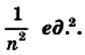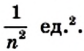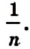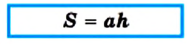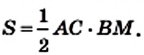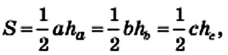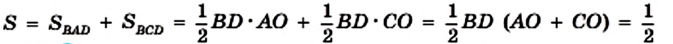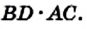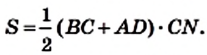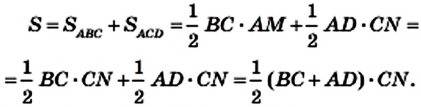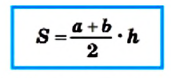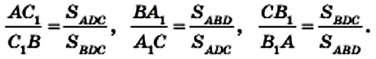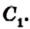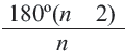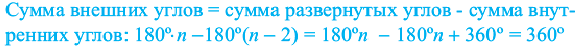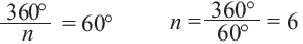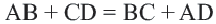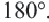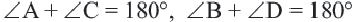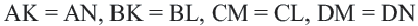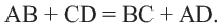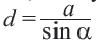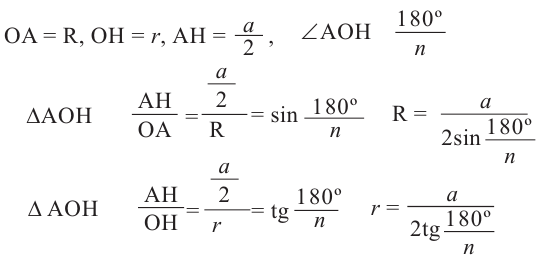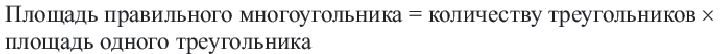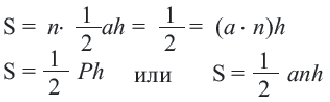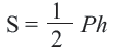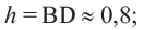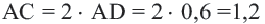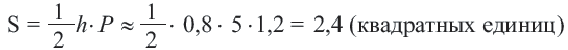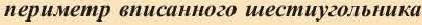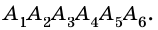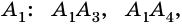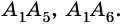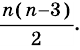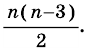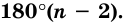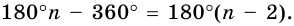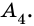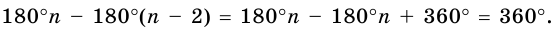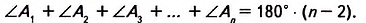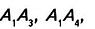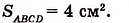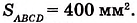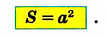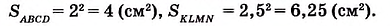Многоугольник составленный из треугольников

Содержание:

Изучив материал этой лекции, вы узнаете формулу, с помощью которой можно найти сумму углов выпуклого многоугольника.

• Вы расширите свои представления о такой знакомой вам величине, как площадь.
• Вы научитесь находить площадь параллелограмма, треугольника, трапеции.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Определение многоугольников

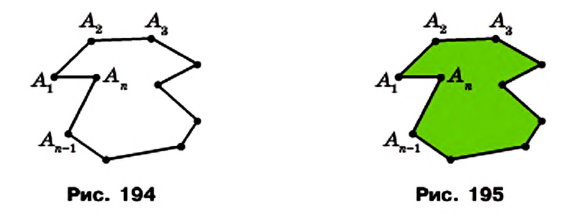
Рассмотрим фигуру, состоящую из точек

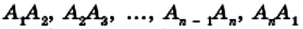
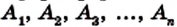
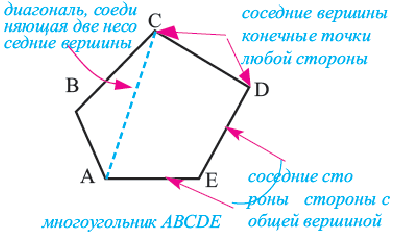
Фигура, образованная этими отрезками, ограничивает часть плоскости, выделенную на рисунке 195 зеленым цветом. Эту часть плоскости вместе с отрезками называют многоугольником. Точки называют вершинами многоугольника, а указанные выше отрезки — сторонами многоугольника.

Стороны, являющиеся соседними отрезками, называют соседними сторонами многоугольника. Вершины, являющиеся концами одной стороны, называют соседними вершинами многоугольника.

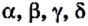
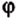
Две соседние стороны многоугольника образуют угол многоугольника. Например, на рисунке 196 — углы многоугольника, а не является углом многоугольника.

Многоугольник называют по количеству его углов: треугольник, четырехугольник, пятиугольник и т. п.

Многоугольник обозначают по его вершинам. Например, на рисунке 197 изображен пятиугольник ABCDE. В обозначении многоугольника буквы, стоящие рядом, соответствуют соседним вершинам. Например, пятиугольник, изображенный на рисунке 197, можно обозначить еще и так: CDEAB, EABCD, EDCBA и т. д.

Периметром многоугольника называют сумму длин всех его сторон.

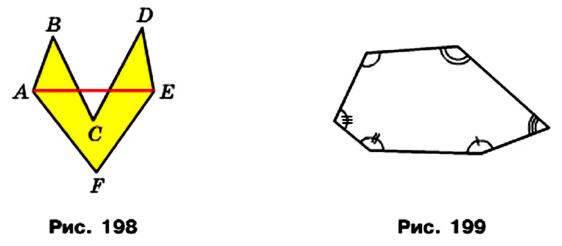
Отрезок, соединяющий несоседние вершины многоугольника, называют диагональю. Например, на рисунке 198 отрезок АЕ — диагональ шестиугольника ABCDEF.

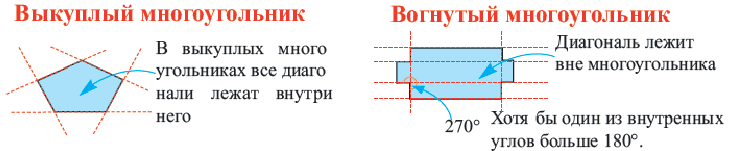
На рисунке 199 изображен многоугольник, все углы которого меньше развернутого. Такой многоугольник называют выпуклым. Из сказанного следует, что любой треугольник является выпуклым многоугольником. Заметим, что многоугольники, изображенные на рисунках 196-198, не являются выпуклыми.

Выпуклый многоугольник обладает такими свойствами:

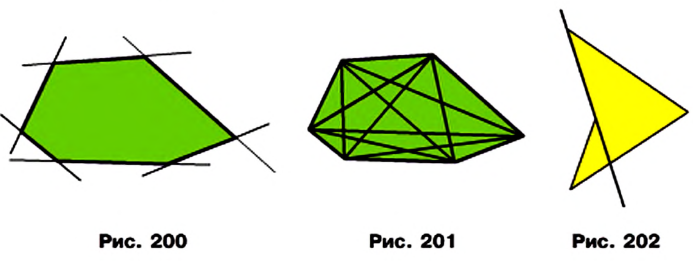
1. выпуклый многоугольник расположен в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 200);
2. выпуклый многоугольник, отличный от треугольника, содержит любую свою диагональ (рис. 201).

Если многоугольник не является выпуклым, то он такими свойствами не обладает (рис. 198, 202).

Теорема 19.1. Сумма углов выпуклого n-угольника равна

Доказательство. Для случая n = 3 теорема была доказана в 7 классе (теорема 16.1).

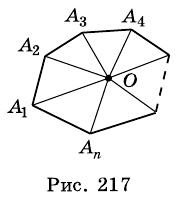
Пусть 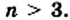На рисунке 203 изображен выпуклый n-угольник

Докажем, что сумма всех его углов равна 180° (n-2).

Проведем все его диагонали, выходящие из вершины 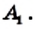Эти диагонали разбивают данный многоугольник на (n — 2) треугольника. Сумма всех углов этих треугольников равна сумме углов n-угольника. Поскольку сумма углов каждого треугольника равна 180°, то искомая сумма равна 180° (n — 2).

Отметим, что эта теорема справедлива и для любого многоугольника, не являющегося выпуклым.

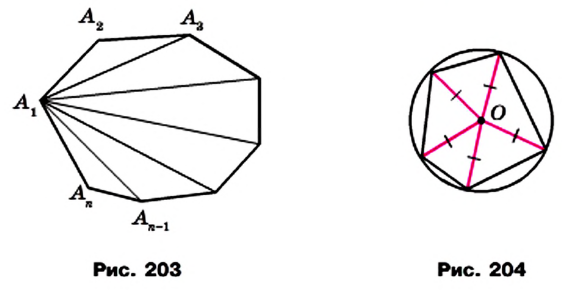
Определение. Окружность называют описанной около многоугольника, если она проходит через все его вершины.

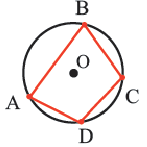
На рисунке 204 изображена окружность, описанная около многоугольника. В этом случае также говорят, что многоугольник вписан в окружность.

Центр окружности, описанной около многоугольника, равноудален от всех его вершин. Следовательно, этот центр принадлежит серединным перпендикулярам всех сторон многоугольника, вписанного в окружность.

Около многоугольника можно описать окружность, если существует точка, равноудаленная от всех его вершин. Следовательно, если серединные перпендикуляры всех сторон многоугольника пересекаются в одной точке, то около такого многоугольника можно описать окружность.

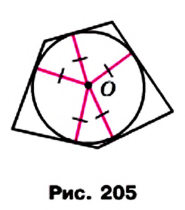
Определение. Окружность называют вписанной в многоугольник, если она касается всех его сторон.

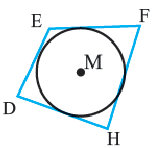
На рисунке 205 изображена окружность, вписанная в многоугольник. В этом случае также говорят, что многоугольник описан около окружности.

Центр окружности, вписанной в многоугольник, равноудален от всех его сторон. Следовательно, этот центр принадлежит биссектрисам всех углов многоугольника, описанного около окружности.

Понятие площади многоугольника. Площадь прямоугольника

С такой величиной, как площадь, вы часто встречаетесь в повседневной жизни: площадь квартиры, площадь дачного участка, площадь поля и т. п.

Опыт подсказывает вам, что равные земельные участки имеют равные площади, что площадь квартиры равна сумме площадей всех ее помещений (комнат, кухни, коридора и т. д.).

Вы знаете, что площади земельных участков измеряют в сотках (арах) и гектарах; площади регионов и государств — в квадратных километрах; площадь квартиры — в квадратных метрах.

На этих практических знаниях о площади основывается определение площади многоугольника.

Определение. Площадью многоугольника называют положительную величину, которая обладает следующими свойствами:

1. равные многоугольники имеют равные площади;
2. если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3. за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.

Измерить площадь многоугольника — это значит сравнить его площадь с площадью единичного квадрата. В результате получают числовое значение площади данного многоугольника. Это число показывает, во сколько раз площадь данного многоугольника отличается от площади единичного квадрата.

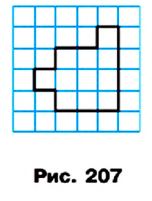
Например, если клетку вашей тетради принять за единичный квадрат, то площадь многоугольника, изображенного на рисунке 207, будет равна 11 квадратным единицам (кратко записывают: 11 ед. 2 ).

Обычно для нахождения площади используют формулы, то есть вычисляют площадь многоугольника по определенным элементам (сторонам, диагоналям, высотам и т. д.). Некоторые из формул вы уже знаете. Например, вы неоднократно применяли формулу S = ab, где S — площадь прямоугольника, а и b — длины его соседних сторон.

Для доказательства этой формулы потребуется следующая лемма.
Лемма. Площадь квадрата со стороной 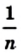ед. (n — натуральное число) равна

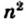
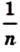
Доказательство. Рассмотрим единичный квадрат и разделим его на равных квадратов со стороной (рис. 208).
Из определения площади многоугольника (свойство 1) следует, что все эти квадраты имеют равные площади. По свойству 2 сумма площадей этих квадратов равна площади единичного квадрата, то есть 1 ед. 2 . Поэтому площадь каждого маленького квадрата равна

Теорема 20.1. Площадь прямоугольника равна произведению длин его соседних сторон.

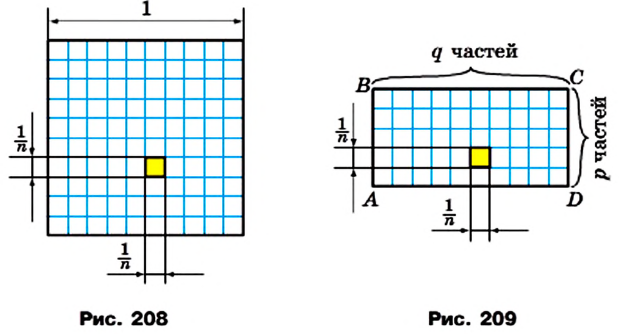
Доказательство. На рисунке 209 изображен прямоугольник ABCD, длины соседних сторон которого равны a и b: АВ = а, ВС = b. Докажем для случая, когда а и b — рациональные числа, что площадь S прямоугольника вычисляют по формуле S = ab.

Числа а и b представим в виде обыкновенных дробей с одинаковыми знаменателями:
где — натуральные числа.
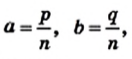
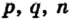
Разделим сторону АВ на р равных частей, а сторону ВС — на q равных частей. Через точки деления проведем прямые, параллельные сторонам прямоугольника. Тогда прямоугольник будет разделен на 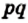равных квадратов со стороной

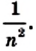
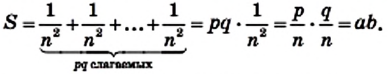
Согласно лемме площадь каждого квадрата равна Из определения площади (свойство 2) следует, что площадь прямоугольника равна сумме площадей всех квадратов, то есть
Рассмотрение случая, когда хотя бы одно из чисел а или b является иррациональным, выходит за рамки школьного курса геометрии.

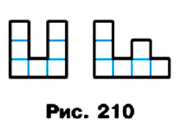
Определение. Многоугольники, имеющие равные площади, называют равновеликими.

Из определения площади (свойство 1) следует, что все равные фигуры равновелики. Однако не все фигуры, имеющие равные площади, являются равными. Например, на рисунке 210 изображены два многоугольника, каждый из которых составлен из семи единичных квадратов. Эти многоугольники равновелики, но не равны.

Площадь параллелограмма

Теорема 21.1. Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.

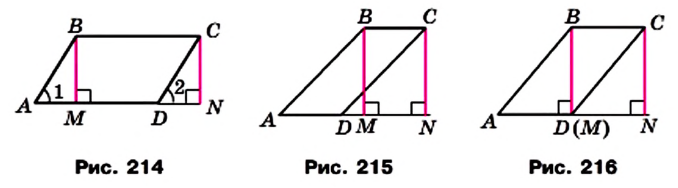
Доказательство. На рисунке 214 изображены параллелограмм ABCD, площадь которого равна S, и его высота ВМ. Докажем, что S = ВС • ВМ.

Проведем высоту CN. Легко показать (сделайте это самостоятельно), что четырехугольник MBCN — прямоугольник. Покажем, что он равновелик данному параллелограмму.

Площадь параллелограмма равна сумме площадей треугольника АВМ и трапеции MBCD. Площадь прямоугольника равна сумме площадей указанной трапеции и треугольника DCN. Однако треугольники АВМ и DCN равны по гипотенузе и острому углу (отрезки АВ и CD равны как противолежащие стороны параллелограмма, углы 1 и 2 равны как соответственные при параллельных прямых АВ и DC и секущей AD). Значит, эти треугольники равновелики. Отсюда следует, что параллелограмм ABCD и прямоугольник MBCN равновелики.

По теореме 20.1 площадь прямоугольника MBCN равна произведению длин сторон ВС и ВМ. Тогда S = ВС • ВМ, где S — площадь параллелограмма ABCD.

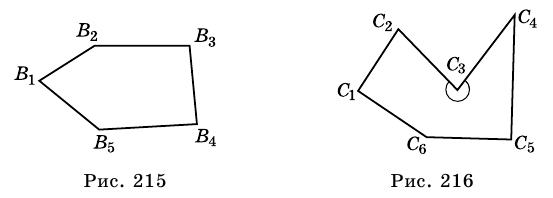
Для завершения доказательства надо рассмотреть случаи, когда основание М высоты ВМ не будет принадлежать стороне AD (рис. 215) или совпадет с вершиной D (рис. 216). И в этом случае параллелограмм ABCD и прямоугольник MBCN будут равновеликими. Докажите этот факт самостоятельно.

Если обозначить длины стороны параллелограмма и проведенной к ней высоты соответственно буквами а и h, то площадь S параллелограмма вычисляют по формуле

Площадь треугольника

Теорема 22.1. Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.

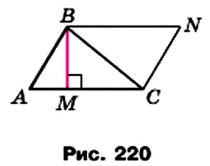
Доказательство. На рисунке 220 изображены треугольник АВС, площадь которого равна S, и его высота ВМ. Докажем, что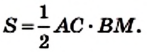
Через вершины В и С треугольника проведем прямые, параллельные сторонам АС и АВ соответственно (рис. 220). Пусть эти прямые пересекаются в точке N. Четырехугольник ABNC — параллелограмм по определению. Треугольники АВС и NCB равны (докажите это самостоятельно). Следовательно, равны и их площади. Тогда площадь треугольника АВС равна половине площади параллелограмма ABNC. Высота ВМ треугольника АВС является также высотой параллелограмма
ABNC. Отсюда

Если воспользоваться обозначениями для высот и сторон треугольника АВС, то согласно доказанной теореме имеем:

где S — площадь треугольника.

Следствие. Площадь прямоугольного треугольника равна половине произведения его катетов.

Докажите эту теорему самостоятельно.

Пример №1

Докажите, что площадь ромба равна половине произведения его диагоналей.

Решение:

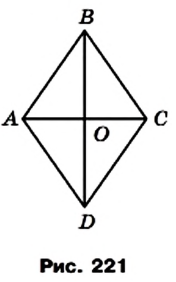
На рисунке 221 изображен ромб ABCD, площадь которого равна S. Его диагонали АС и BD пересекаются в точке О. Докажем, что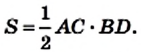
Поскольку диагонали ромба перпендикулярны, то отрезки АО и СО являются высотами треугольников BAD и BCD соответственно. Тогда можно записать:

Площадь трапеции

Теорема 23.1. Площадь трапеции равна произведению полусуммы ее оснований и высоты.

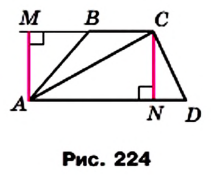
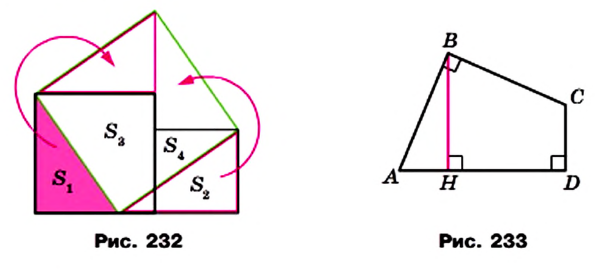
Доказательство. На рисунке 224 изображена трапеция ABCD (AD||BC), площадь которой равна S. Отрезок CN — высота этой трапеции. Докажем, что

Проведем диагональ АС и высоту AM трапеции. Отрезки AM и CN являются высотами треугольников АВС и ACD соответственно.

Имеем:

Если обозначить длины оснований трапеции и ее высоты соответственно буквами 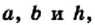то площадь S трапеции вычисляют по формуле

Следствие. Площадь трапеции равна произведению ее средней линии и высоты.

Равносоставленные и равновеликие многоугольники

Если некоторый многоугольник можно разрезать на части и составить из них другой многоугольник, то такие два многоугольника называют равносоставленными.

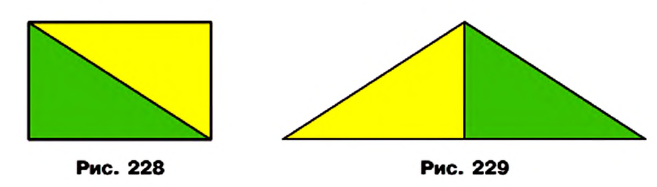
Например, если прямоугольник разрезать вдоль его диагонали (рис. 228), то получим два равных прямоугольных треугольника, из которых можно составить равнобедренный треугольник (рис. 229). Фигуры на рисунках 228 и 229 — равно составленные.

Очевидно, что равносоставленные многоугольники являются равновеликими. Этот факт применяют при доказательстве теорем и решении задач. Например, доказывая теорему 21.1, мы фактически разрезали параллелограмм на треугольник АВМ и трапецию MBCD, из которых составили прямоугольник MBCN (см. рис. 215).

Если треугольник разрезать вдоль средней линии, то из полученных треугольника и трапеции можно составить параллелограмм (рис. 230).

Легко установить (сделайте это самостоятельно), что такое разрезание треугольника приводит к еще одному доказательству теоремы о площади треугольника (теорема 22.1). Этой же цели служит разрезание треугольника на части, из которых можно составить прямоугольник (рис. 231).

Евклид в своей знаменитой книге «Начала» формулирует теорему Пифагора так:

«Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах».

Если показать, что можно разрезать квадраты, построенные на катетах, на части и составить из этих частей квадрат со стороной, равной гипотенузе, то тем самым будет доказана теорема Пифагора.

На рисунке 232 показан один из возможных способов такого разрезания. Квадраты, построенные на катетах, разрезаны на части, площади которых равны 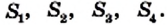Из этих частей сложен квадрат, построенный на гипотенузе.

Из определения площади многоугольника следует, что равносоставленные многоугольники являются равновеликими. Но совсем неочевидной является такая теорема.

Теорема. Любые два равновеликих многоугольника являются равносоставленными.

Впервые этот факт доказал в 1832 г. венгерский математик Фаркаш Бойяи. Позднее немецкий математик Пауль Гервин нашел другое доказательство. Поэтому эту теорему называют теоремой Бойяи—Гервина.

Теорема Чевы

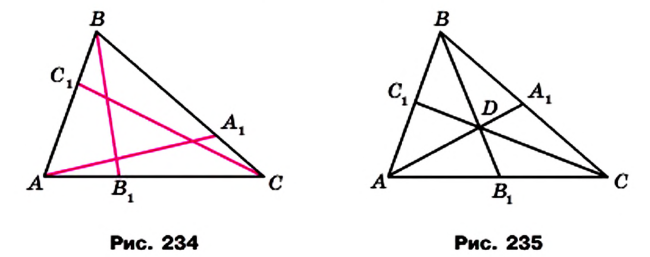
На сторонах ВС, СА и АВ треугольника АВС отметим произвольные точки 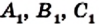(рис. 234). Каждый из отрезков АЛ,, BBV СС, называют чевианой треугольника АВС. Такое название связано с именем итальянского инженера и математика Джованни Чевы (1648-1734), открывшего удивительную теорему.

Если точки 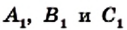выбраны так, что чевианы являются биссектрисами, либо медианами, либо высотами остроугольного треугольника, то эти чевианы пересекаются в одной точке.

Если три прямые пересекаются в одной точке, то их называют конкурентными.

Теорема Чевы дает общий критерий конкурентности произвольных трех чевиан.

Теорема. Для того чтобы, чевианы 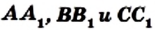треугольника АВС пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство

Доказательство. Докажем сначала необходимое условие конкурентности: если чевианы 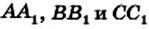пересекаются в одной точке, то выполняется равенство (*).

Воспользовавшись результатом ключевой задачи 757, можно записать (рис. 235):

Перемножив записанные равенства, получим равенство (*).

Докажем теперь достаточное условие конкурентности: если выполняется равенство (*), то чевианы 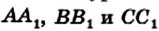пересекаются в одной точке.

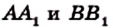
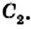
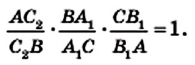
Пусть чевианы пересекаются в точке D, а чевиана, проходящая через вершину С и точку D, пересекает сторону АВ в некоторой точке Из доказанного выше можно записать:

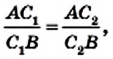
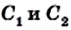
Сопоставляя это равенство с равенством (*), приходим к выводу, что то есть точки делят отрезок АВ в одном и том же отношении, а значит, эти точки совпадают. Следовательно, прямая CD пересекает сторону АВ в точке

Напомню:

Сумма углов выпуклого n-угольника
Сумма углов выпуклого n-угольника равна 180° (n — 2).

Окружность, описанная около многоугольника
Окружность называют описанной около многоугольника, если она проходит через все его вершины.

Окружность, вписанная в многоугольник
Окружность называют вписанной в многоугольник, если она касается всех его сторон.

Площадь многоугольника
Площадью многоугольника называют положительную величину,
которая обладает следующими свойствами:

1. равные многоугольники имеют равные площади;
2. если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3. за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.

Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон.

Равновеликие многоугольники
Многоугольники, имеющие равные площади, называют равновеликими.

Площадь параллелограмма
Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.

Площадь треугольника
Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.

Площадь прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь трапеции

• Площадь трапеции равна произведению полусуммы ее оснований и высоты.
• Площадь трапеции равна произведению ее средней линии и высоты.

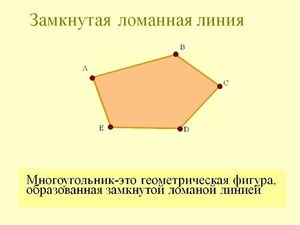
Ломанная линия и многоугольники

Ломаная линия состоит из таких нескольких последовательно-соединенных отрезков: конец первого является началом второго, конец второго является началом третьего и т.д. Если конечная точка последнего отрезка совпадает с начальной точкой первого отрезка, то ломаная называется замкнутой. Многоугольник — это фигура, образованная замкнутой ломаной линией, в которой смежные отрезки не лежат на одной прямой, а несмежные — не пересекаются.

• Многоугольник — это плоская фигура.
• Стороны состоят из конечного числа отрезков.
• Многоугольник это замкнутая фигура, делящая плоскость на 2 части: внутреннюю замкнутую область и внешнюю бесконечную область.
• Многоугольник обозначают буквами, указывающими его вершины.

Многоугольники бывают выпуклые и вогнутые. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой содержащей его сторону. Если не лежит в одной полуплоскости — вогнутым.

Многоугольник называется правильным, если у него все стороны все углы конгруэнтны.

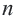
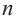
В многоугольнике количество вершин, сторон и углов одинаковые. Многоугольник с — сторонами называют еще и — угольным.

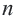
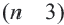
Соответственно количеству сторон, многоугольники называются треугольными, четырехугольными, пятиугольными, шестиугольными т.д. Из любой вершины выпуклого — угольника выходят диагонали.

Внутренние и внешние углы многоугольника

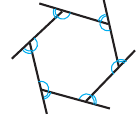
Угол, образованный двумя сторонами, исходящими из данной вершины называется внутренним углом при данной’ вершине выпуклого многоугольника. Угол, смежный с внутренним углом многоугольника называется внешним. Сумма внутренних и внешних углов (взятых по одному при каждой вершине) многоугольника при любой вершине равна .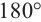

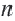
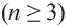
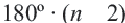
Теорема 1. Сумма внутренних углов выкуплого — угольника равна .

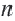
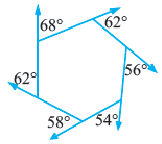
Следствие: Каждый внутренний угол правильного — угольника равен

Теорема 2. Сумма внешних углов выкуплого многоугольника равен .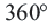

Следствие 2. Каждый внешний угол правильного 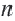— угольника равен .

Пример №2

Один из внешних углов правильного многоугольника равен .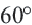

a) найдите градусную меру внутреннего угла многоугольника;

b) найдите число сторон многоугольника.

Решение: а) ;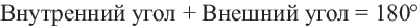

Внутренний угол:

b)

Многоугольники вписанные в окружность и описанные около окружности

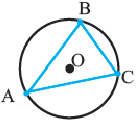
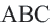
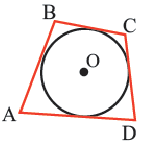
Определение 1. Многоугольник называется вписанным в окружность, если все его вершины лежат на окружности, а окружность называется описанной около многоугольника. На рисунке треугольник вписан в окружность.

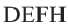
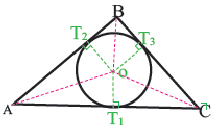
Определение 2. Многоугольник называется описанным около окружности, если все его стороны касаются окружности, а окружность называется вписанной в многоугольник. На рисунке четырехугольник описан около окружности.

Окружность, вписанная в треугольник и описанная около нее

Теорема 1. В любой треугольник можно вписать окружность. Центром этой окружности будет точка пересечения биссектрис углов треугольника.

Теорема 2. Около любого треугольника можно описать окружность. Центром этой окружности будет точка пересечения серединных перпендикуляров к сторонам треугольника.

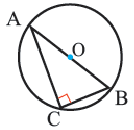
Теорема 3. Если в окружность вписан прямоугольный треугольник, то гипотенуза является диаметром этой окружности.

Обратная теорема. Если сторона треугольника, вписанного в окружность, является диаметром, то этот треугольник — прямоугольный.

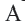
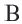
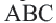
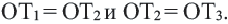
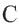
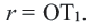
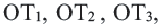
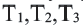
Доказательство 1-ой теоремы (текстовое). Проведем биссектрисы углов и треугольника и точку пересечения обозначим буквой . Произвольная точка, взятая на биссектрисе находится на одинаковом расстоянии от сторон угла. Поэтому Точка находится и на биссектрисе угла (почему?). Нарисуем окружность с центром в точке и радиусом Так как стороны треугольника перпендикулярны радиусам то в точках они касаются окружности. А значит, эта окружность является вписанной в треугольник.

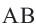
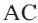
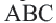
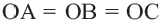
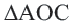
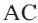
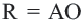
Доказательство 2-ой теоремы. Через середины сторон и треугольника проведем перпендикуляры и точку их пересечения обозначим буквой . По свойству серединного перпендикуляра к отрезку . Так как равнобедренный, то точка находится и на серединном перпендикуляре стороны . Окружность с центром в точке и радиусом , пройдя через все вершины треугольника, будет описанной около нее.

Замечание: Около данного треугольника можно описать только одну окружность. В данную окружность можно вписать бесконечное количество треугольников.

Свойства четырехугольников, вписанных в окружность и описанного около нее

В отличие от треугольников, не во всякий четырехугольник можно вписать или описать окружность.

Теорема 4. В любом описанном четырехугольнике суммы противоположных сторон равны.

Обратная теорема. Если суммы противоположных сторон четырехугольника равны, то в этот четырехугольник можно вписать окружность.

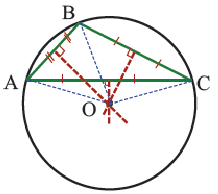
Теорема 5. Сумма двух противоположных углов четырехугольника, вписанного в окружность, равна

Обратная теорема. Если сумма противоположных углов четырехугольника равна 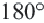, то около этого четырехугольника можно описать окружность.

Доказательство теоремы 4: Пусть точки 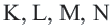будут точками касания сторон четырехугольника. По свойству касательных, проведенных из данной точки к окружности,

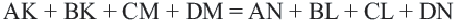
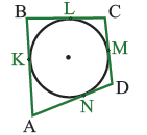
Если сложить почленно эти равенства, получим или же

Отношение стороны треугольника, вписанного в окружность, к синусу противолежащего угла равно диаметру этой окружности:

Исследуйте данное доказательство для случая, когда центр окружности расположен внутри треугольника, обсудите и напишите в тетради.

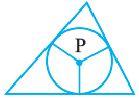
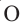
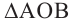
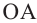
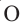
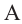
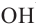
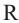
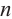
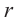
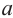
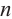
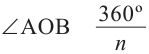
В любой правильный многоугольник можно вписать и описать окружность. Центры этих окружностей совпадут. Биссектрисы углов правильного многоугольника пересекаются в точке и образуют равнобедренные треугольники конгруэнтные показанному на рисунке (по признаку УСУ). Нарисуем окружность радиусом с центром в точке . Эта окружность, пройдя через все вершины, будет описанной окружностью. окружность с радиусом , касаясь всех сторон многоугольника, будет вписанной окружностью. — радиус окружности, описанной около правильного -угольника, -радиус вписанной окружности, -сторона правильного -угольника, — центральный угол

Задача на построение: Постройте правильный шестиугольник.

1. Нарисуйте отрезок , равный стороне правильного шестиугольника.

2. Циркулем нарисуйте окружность, радиус которой равен длине этого отрезка.

3. Не меняя раствора циркуля, разбейте всю окружность на части одинаковой длины и отметьте их точками.

4. Соедините последовательно отмеченные точки. Получится правильный шестиугольник, вписанный в окружность.

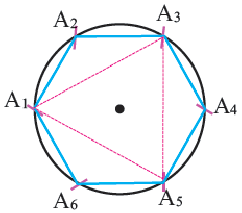
Если соединить попарно некоторые вершины правильного шестиугольника , например, вершины , то получится правильный треугольник. Чтобы построить правильный четырехугольник, нужно провести два взаимно перпендикулярных диаметра и последовательно соединить их концы. Если в окружность вписан правильный — угольник, то отметив точки пересечения серединных перпендикуляров с окружностью, получим точки являющиеся вершинами правильного -угольника.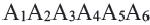

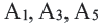
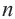
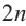
Площадь правильного многоугольника

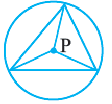
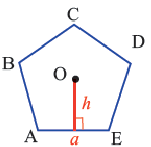
Центр правильного многоугольника. Центр окружности, описанного около правильного многоугольника или вписанного в него, является центром правильного многоугольника. Центр правильного многоугольника находится на одинаковом расстоянии от всех вершин и всех сторон многоугольника.

Апофема правильного многоугольника. Перпендикуляр, проведенный из центра многоугольника к его стороне, называется апофемой. Апофема правильного многоугольника равна радиусу вписанной окружности.

Выполните следующее упражнение по шагам и выведите формулу зависимости площади правильного многоугольника от апофемы.

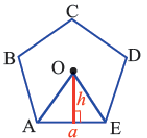
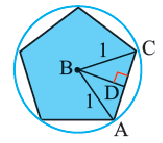
1. Нарисуйте правильный пятиугольник .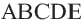

2. Из центра 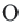проведите перпендикуляр, делящий сторону пополам.

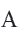
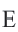
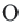
3. Соедините точки и с центром .

4. Выразите площадь треугольника переменными и . Обратите внимание какому измерению многоугольника соответствует высота треугольника.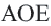

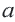
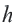
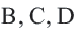
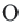
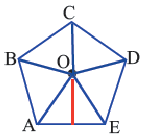
5. Соедините точки с точкой . Сравните площади полученных треугольников.

6. Обратите внимание на то, что площадь пятиугольника равна сумме площадей этих треугольников. Площадь пятиугольника:

7. Какому измерению соответствует выражение ? Выразите площадь пятиугольника через его периметр.

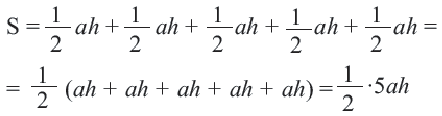
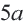
Площадь правильного многоугольника:

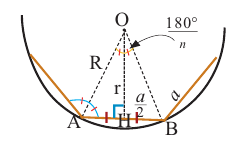
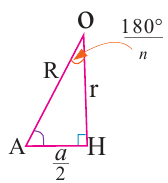
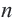
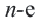
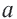
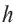
Соединив центр правильного -угольника с вершинами, получится количество равнобедренных конгруэнтных треугольников.

-длина стороны многоугольника , -число сторон, -апофема.

Пример №3

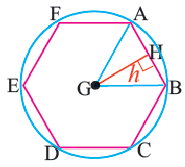
В окружность радиусом равным единице, вписан правильный пятиугольник. Найдите площадь пятиугольника. Решение:

Площадь многоугольника:

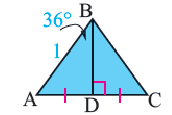
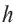
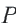
Нужно найти апофему и периметр .

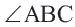
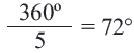
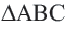
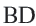
Центральный угол равен . — равнобедренный треугольник, а значит его высота является и медианой, и биссектрисой.

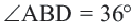
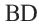
Тогда . Чтобы найти стороны треугольника , воспользуемся тригонометрическими соотношениями .

— апофема пятиугольника,

Сторона пятиугольника:

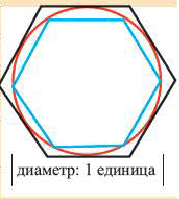
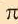
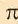
Историческое сведение. В 3-ем веке до н.э. Архимед — древнегреческий ученый, для того, чтобы определить численное значение , воспользовался периметрами правильных; многоугольников описанных и вписанных в окружность. Пользуясь данным способом исследуйте значение .

1. Принимая за единицу диаметр окружности, найдите периметр вписанного шестиугольника.

2. Покажите, что длина окружности с единичным диаметром равна .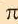

3. Нарисуйте радиус окружности. Найдите периметр описанного шестиугольника.

4. Напишите неравенство: .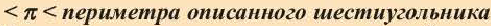

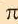
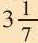
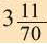
Увеличив число сторон многоугольника в 2 раза и продолжая вычисления для 12-ти, а затем для 96-ти угольного многоугольника Архимед, определил, что значения больше , но меньше .

Паркетирование

Паркетированием называется покрытие площади фигурами до заполнения всей пустоты.

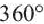
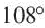
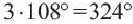
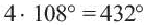
Если сумма углов при общей вершине многоугольника равна , то паркетированием можно покрыть всю пустую часть площади. Паркетирование возможно при помощи правильных треугольников, ромбов (квадратов) и правильных шестиугольников. Однако, при помощи правильных пятиугольников это сделать невозможно, потому что, градусная мера одного угла равна , а сумма углов при общей вершине трех пятиугольников , а четырех пятиугольников .

Справочный материал по многоугольникам

Многоугольник и его элементы.

Сумма углов выпуклого многоугольника. многоугольник, вписанный в окружность, и многоугольник, описанный около окружности.

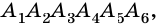
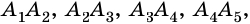
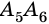
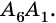
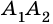
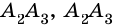
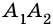
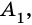
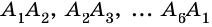
Рассмотрим фигуру изображенную на рисунке 213. Она состоит из отрезков и При этом отрезки размещены так, что соседние отрезки ( и и и ) не лежат на одной прямой, а несоседние отрезки не имеют общих точек. Такую фигуру называют многоугольником. Точки называют вершинами многоугольника, а отрезки — сторонами многоугольника.

Очевидно, что количество вершин многоугольника равно количеству его сторон.

Сумму длин всех сторон многоугольника называют его периметром.

Наименьшее количество вершин (сторон) у многоугольника — три. В этом случае имеем треугольник. Еще одним отдельным видом многоугольника является четырехугольник.

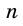
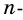
Многоугольник, у которого вершин, называют угольником. На рисунке 213 изображен шестиугольник

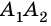
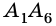
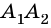
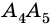
Две стороны многоугольника называют соседними, если они имеют общую вершину. Стороны многоугольника, не имеющие общей вершины, называют несоседними. Например, стороны и — соседние, a и — несоседние (рис. 213).

Две вершины многоугольника называют соседними, если они принадлежат одной стороне, а вершины многоугольника, не принадлежащие одной стороне, называют несоседними.

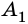
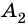
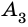
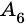
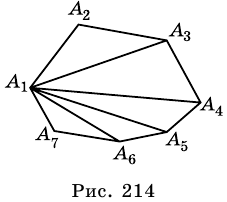
Например, вершины и — соседние, и — несоседние (рис. 213).

Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. На рисунке 214 изображены диагонали многоугольника 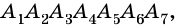выходящие из вершины

Пример №4

Сколько диагоналей имеет 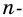угольник?

Решение:

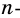
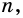
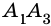
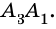
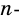
Из каждой вершины угольника выходит диагонали. Всего вершин а каждая диагональ повторяется дважды, например и Поэтому всего диагоналей у угольника будет

Ответ.

Углы, стороны которых содержат соседние стороны многоугольника, называют углами многоугольника. Пятиугольник 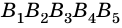имеет углы

Если каждый из углов многоугольника меньше развернутого, то такой многоугольник называют выпуклым. Если хотя бы один угол многоугольника больше развернутого, то такой многоугольник называют невыпуклым.

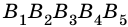
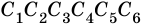
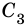
Многоугольник — выпуклый (рис. 215), а многоугольник — невыпуклый (рис. 216), так как угол при вершине больше чем 180°.

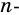
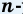
Теорема (о сумме углов выпуклого угольника). Сумма углов выпуклого угольника равна

Доказательство:

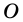
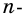
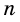
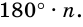
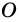
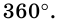
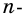
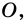
Выберем во внутренней области многоугольника произвольную точку и соединим ее со всеми вершинами угольника (рис. 217). Получим треугольников, сумма всех углов которых равна Сумма углов с вершиной в точке равна Сумма углов данного угольника равна сумме углов всех треугольников, кроме углов с вершиной в точке то есть:

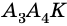
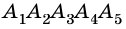
Углы выпуклого многоугольника называют еще его внутренними углами. Угол, смежный с внутренним углом многоугольника, называют внешним углом многоугольника. На рисунке 218 угол — внешний угол многоугольника — при вершине

Очевидно, что каждый многоугольник имеет по два внешних угла при каждой вершине.

Пример №5

Докажите, что сумма внешних углов выпуклого 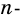угольника, взятых по одному при каждой вершине, равна 360°.

Решение:

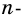
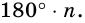
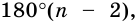
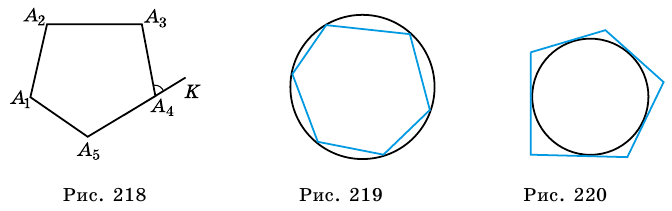
Сумма внутреннего и внешнего углов при каждой вершине многоугольника равна 180°. Поэтому сумма всех внутренних и внешних углов угольника равна Так как сумма внутренних углов равна то сумма внешних углов равна:

Многоугольник называют вписанным в окружность, если все его вершины лежат на окружности. Окружность при этом называют описанной около многоугольника (рис. 219).

Около многоугольника не всегда можно описать окружность. Если же это возможно, то центром такой окружности является точка пересечения серединных перпендикуляров к сторонам многоугольника (как и в случае треугольника).

Многоугольник называют описанным около окружности, если все его стороны касаются окружности. Окружность при этом называют вписанной в многоугольник (рис. 220).

Не в каждый многоугольник можно вписать окружность. Если же это возможно, то центром такой окружности является точка пересечения биссектрис внутренних углов многоугольника (как и в случае треугольника).

Многоугольник и его свойства

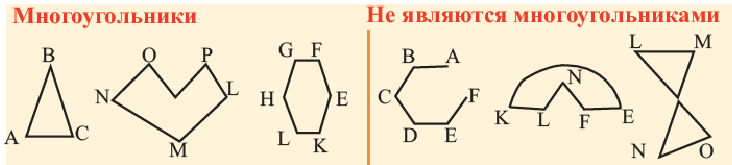
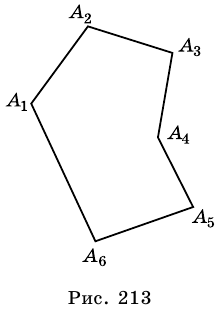
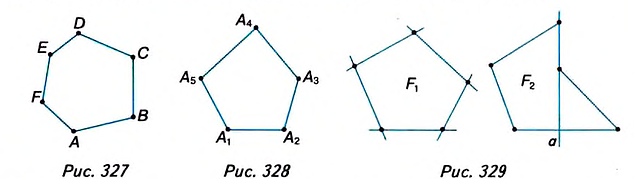
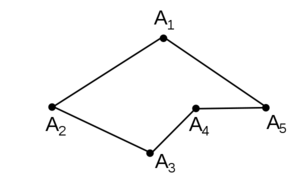
Вы уже знаете, что такое треугольник и четырёхугольник. Более общим является понятие многоугольника. На рисунке 327 вы видите многоугольник ABCDEF. Он состоит из отрезков АВ, ВС, CD, DE, EFy FA, размещённых таким образом, что смежные отрезки не лежат на одной прямой, а несмежные -не имеют общих точек. Отрезки, из которых состоит многоугольник, называются его сторонами, углы, образованные смежными сторонами, — углами, а вершины этих углов — вершинами многоугольника.

В зависимости от количества вершин (углов либо сторон) многоугольник называется треугольником, четырёхугольником, пятиугольником и т. д. Многоугольник с n вершинами называется n-угольником.

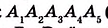
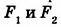
Многоугольник обозначают названиями его вершин, например шестиугольник ABCDEF (рис. 327), пятиугольник (рис. 328). ? | На рисунке 329 вы видите многоугольники . В чём их различие?

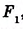
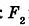
Ни одна из прямых, проходящих через стороны многоугольника не пересекает другие его стороны. Он лежит по одну сторону от любой из этих прямых. Такой многоугольник называется выпуклым. Многоугольник не является выпуклым.

В дальнейшем мы будем рассматривать лишь выпуклые многоугольники.

Периметром многоугольника называется сумма длин всех его сторон. Его обозначают буквой Р.

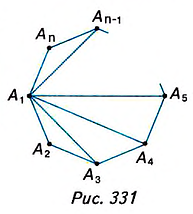
Посмотрите на рисунок 330. В шестиугольнике ABCDEF отрезки AC, AD, АЕ соединяют вершину А с несоседними вершинами. Это — диагонали шестиугольника.

Диагональю n-угольника называется отрезок, который соединяет две несоседние его вершины.

Теорема (о сумме углов n-угольника).

Сумма углов n-угольника равна 180° • (n — 2).

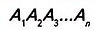
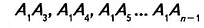
Дано: — n-угольник (рис. 331), — диагонали. Доказать:

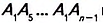
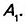
Доказательство. В заданном n-угольнике диагонали выходят из одной вершины Поэтому они разбивают n-угольник на n — 2 треугольников. Сумма всех углов образованных треугольников равна сумме углов данного n-угольника. Поскольку в каждом треугольнике сумма углов равна 180°, то сумма углов данного n-угольника — 180° • (n — 2).

Угол, смежный с углом многоугольника (рис. 332), называется внешним углом многоугольника.

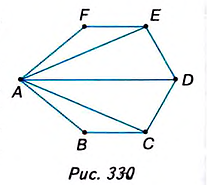
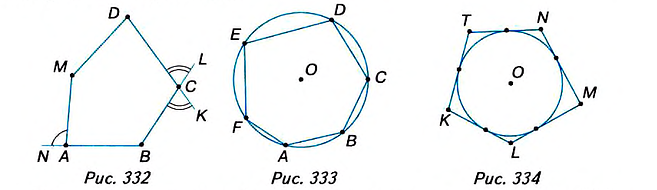
Многоугольники могут быть вписанными в окружность (рис. 333) или описанными около окружности (рис. 334). Попытайтесь дать определения и сравните их с указанными в учебнике.

Многоугольник все вершины которого лежат на окружности, называется вписанным, в эту окружность, а окружность — описанной около этого многоугольника.

Многоугольнику все стороны которого касаются окружности, называется описанным около этой окружности, а окружность — вписанной в этот многоугольник.

Стороны вписанного многоугольника и его диагонали — это хорды окружности. Каждый его угол является вписанным углом (рис. 335).

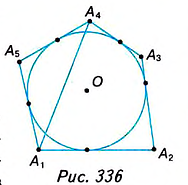
Стороны описанного многоугольника являются касательными к окружности, а его диагонали — секущими (рис. 336).

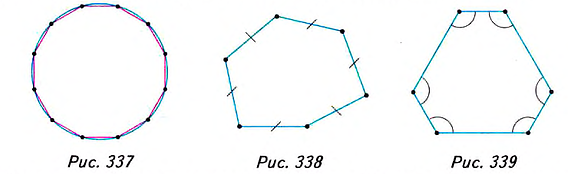
1. Геометрическая фигура называется простой, если её можно разбить на конечное количество треугольников. Многоугольник — это простая фигура (см. рис. 330 и 331), а окружность не является простой фигурой (рис. 337). Даже вписав в окружность многоугольник с очень большим количеством сторон, мы только приблизим его контур к окружности. Поэтому в геометрии длину окружности и площадь круга находят другими методами, чем периметр и площадь многоугольника.

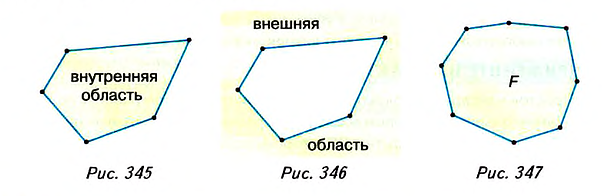
2. У вас может возникнуть вопрос: Всегда ли из равенства сторон многоугольника следует равенство его углов и наоборот? Нет, это свойство лишь треугольника. Вы знаете пример четырёхугольника, в котором все стороны равны, а углы — не равны. Это ромб. В прямоугольнике все углы равны, а вот стороны — нет. Среди многоугольников с большим количеством вершин также можно выделить равносторонние многоугольники, в которых не все углы равны (рис. 338), и равноугольные многоугольники, в которых не все стороны равны

Понятие площади

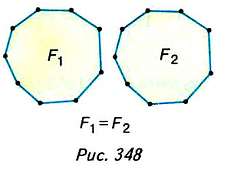
Многоугольник разбивает плоскость на две области — внутреннюю (рис. 345) и внешнюю (рис. 346).

Многоугольник вместе с его внутренней областью называется плоским многоугольником.

Каждый плоский многоугольник (например, многоугольник F на рис. 347) занимает часть плоскости. Если эту часть плоскости выразить некоторым числом, то получим площадь многоугольника. Далее будем говорить «площадь многоугольника», имея в виду, что многоугольник -плоский. Это относится и к другим плоским фигурам.

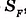
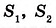
Площадь обозначают буквой S. Иногда указывают название фигуры, например , а для нескольких фигур — индексы, например и т. д.

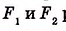
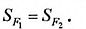
На рисунке 348 фигуры равны, поскольку совмещаются наложением. Понятно, что они имеют равные площади. Можем записать: . Для измерения площади фигуры выбирают единицу измерения. Для этого используют квадрат, со стороной равной единице измерения длины. Площадь квадрата со стороной 1 см — это единица измерения площади в квадратных сантиметрах, со стороной 1 м — в квадратных метрах и т. д.

Единицы измерения площади кратко записываем так: 1 см2, а говорим: «один квадратный сантиметр». Говорить «сантиметр в квадрате» -неправильно!

Некоторые единицы измерения площади имеют специальные названия: ар (квадрат со стороной 10м), гектар (квадрат со стороной 100 м) и т. д.

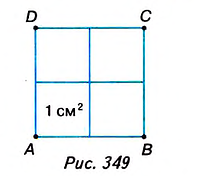
На рисунке 349 вы видите квадрат ABCD со стороной 2 см. Он состоит из четырёх квадратов площадью 1 см2, поэтому его площадь равна 4 см2.

Можем записать:

Ясно, что площадь любой фигуры выражается положительным числом. Изменится ли площадь квадрата ABCD, если за единицу измерения принять 1 мм2? Нет, площадь квадрата не изменится, но будет выражена иначе:

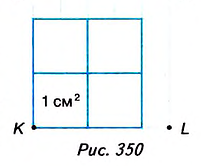
На рисунке 350 длина стороны квадрата KLMN равна 2,5 см. Он вмещает четыре квадрата площадью 1 см2 и ещё 9 маленьких квадратов площадью 0,25 см2. Поэтому 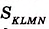= 4 + 9 • 0,25 = 6,25 (см2).

Ясно, что площадь любой фигуры равна сумме площадей частей, из которых она состоит.

Из предыдущих классов вы знаете, что площадь квадрата со стороной а можно вычислить иначе — по формуле площади квадрата:

Для квадратов ABCD и KLMN получим:

Поскольку 4 см2

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Как выглядит замкнутая ломаная линия

Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.

Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:

1. Картография — для построения изображений улиц и схем маршрутов.
2. Архитектура — очертания зданий и строений.
3. Ландшафтный дизайн — декоративное оформление и расположение тропинок.
4. Химия — молекулярная структура сложных полимерных соединений.
5. Медицина — мониторы для контроля функционального состояния органов и систем.

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Типы ломаных линий

Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.

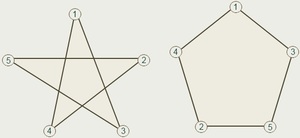
Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.

Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.

Всего существует 4 типа подобных линий по своей структуре:

1. Замкнутые, которые не имеют пересечений.
2. Незамкнутые, которые не имеют пересечений.
3. Незамкнутые самопересекающиеся.
4. Замкнутые, имеющие самопересечения.

Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Особенности замкнутых линий

Рассмотрим подробнее составляющие части этой геометрической фигуры.

1. Один отрезок из тех, что составляют описываемую фигуру, называется ее звеном. Ломаной может считаться такая линия, которую составляют как минимум два отрезка — звена. Если звено одно — это просто единичный отрезок.
2. Существует также понятие вершины ломаной. Этим термином принято называть точку, в которой соединяются концы двух звеньев. Такие точки в геометрии принято обозначать с помощью заглавных латинских букв. Сама ломаная называется сочетанием обозначений этих вершин. Например, названием такой линии может послужить сочетание ABCDEF.
3. Если концы крайних звеньев этого геометрического объекта соединяются в одной точке, такая линия называется замкнутой.
4. Ломаная линия может пересекать саму себя.
5. Конечные вершины такой фигуры в геометрии принято называть черными точками.

Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Многоугольник как разновидность замкнутой ломаной

Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.

1. Если вершины принадлежат одной и той же стороне многоугольника — они носят название смежных.
2. Если отрезок соединяет две любых вершины, не являющиеся смежными, он называется диагональю.
3. Если у многоугольника имеется n вершин — он называется n-угольником. У такой фигуры имеется количество сторон, равное n.
4. Такая ломаная делит плоскость на 2 части — внешнюю и внутреннюю.
5. Если точки многоугольника лежат по одну сторону от прямой и проходят через 2 соседние вершины — его принято называть выпуклым.
6. Угол выпуклого многоугольника при данной вершине — это угол, который образован двумя его сторонами, для которых эта вершина является общей.
7. Внешний угол выпуклого многоугольника при определенной вершине — это угол, смежный с внутренним углом многоугольника при этой же самой вершине.

Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.

Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.

Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.

У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.

Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.

Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.

Видео:Математика 5 Треугольники МногоугольникиСкачать

Многоугольники

Ломаная — это геометрическая фигура, которая состоит из точек,
соединенных отрезками. Отрезки называются звеньями ломаной,
а точки называются вершинами ломаной. Сумма длин всех
звеньев называется длиной ломаной.

Замкнутая ломаная — это ломаная, у которой конец последнего
звена совпадает с началом первого звена.

Простая ломаная — это ломаная, у которой нет пересечений.

Многоугольник — это геометрическая фигура с множеством
углов и сторон, или по другому это простая замкнутая ломаная,
у которой соседние звенья не лежат на одной прямой.

Как и у любой другой геометрической фигуры, у многоугольника
есть стороны и углы. Звенья ломаной называют сторонами
многоугольника, а вершины ломаной называют углами
многоугольника. Периметр многоугольника равен сумме
длин всех сторон многоугольника, или по другому длине ломаной.

Соседние вершины многоугольника — это два угла
многоугольника,принадлежащие одной стороне.

Диагональ многоугольника — это отрезок, соединяющий
две любые не соседних угла.

Произвольный многоугольник разделяет плоскость на две части.
Одна из частей называется внутренней областью, а другая внешней
областью многоугольника. Углы, которые находятся во внутренней
области называются внутренними, соответственно углы, которые
находятся во внешней области называются внешними.

📽️ Видео

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Как найти периметр данной фигуры? Решение за одну минуту!Скачать

Площадь фигурыСкачать

Как начертить треугольник | 4 способа | Выпуклый многоугольникСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Геометрия 10 кл Понятие многогранникаСкачать

Урок 6. Треугольники, четырёхугольники, многоугольники. ОГЭ. Вебинар | МатематикаСкачать

МногоугольникСкачать

Что такое периметр. Как найти периметр многоугольника?Скачать

Видеоурок по математике "Понятие правильного многогранника"Скачать

Многоугольники. 8 класс.Скачать

9 класс. Геометрия. Правильные многоугольники и их свойства. Правильный треугольник. Урок #4Скачать