Maple матрицы и вектора (6 видео) | Курс школьной геометрии

Maple матрицы и вектора

Основная часть команд для решения задач линейной алгебры содержится в библиотеке linalg . Поэтому перед решением задач с матрицами и векторами следует загрузить эту библиотеку командой with(linalg) .

Способы задания векторов.

Для определения вектора в Maple используется команда vector([x1,x2,…,xn]), где в квадратных скобках через запятую указываются координаты вектора. Например:

Координату уже определенного вектора x можно получить в строке вывода, если ввести команду x[i] , где i — номер координаты. Например, первую координату заданного в предыдущем примере вектора можно вывести так:

Вектор можно преобразовать в список и, наоборот, с помощью команды convert(vector, list) или convert(list, vector).

Сложить два вектора a и b можно с помощью двух команд:

Команда add позволяет вычислять линейную комбинацию векторов a и b : , где — скалярные величины, если использовать формат: matadd(a,b,alpha,beta) .

Скалярное, векторное произведение векторов и угол между векторами.

Скалярное произведение двух векторов вычисляется командой dotprod(a,b).

Векторное произведение двух векторов вычисляется командой crossprod(a,b).

Угол между двумя векторами a и b вычисляется с помощью команды angle(a,b) .

Норму (длину) вектора , которая равна , можно вычислить с помощью команды norm(а,2) .

Можно нормировать вектор а с помощью команды normalize(a), в результате выполнения которой будет получен вектор единичной длины .

Нахождение базиса системы векторов. Ортогонализация системы векторов по процедуре Грамма-Шмидта.

Если имеется система n векторов , то с помощью команды basis([a1,a2,…,an]) можно найти базис этой системы.

При помощи команды GramSchmidt([a1,a2,…,an]) можно ортогонализовать систему линейно-независимых векторов .

Содержание

Задание 1.
5. Функции для работы, с векторами и матрицами
Линейная алгебра
Матрицы, векторы и основные операции с ними
🔥 Видео

Видео:Матрицы и векторыСкачать

Задание 1.

1. Даны два вектора: и . Найти и угол между a и b . Для решения этой задачи наберите:

2. Найти векторное произведение , а затем скалярное произведение , где , .

3. Найти норму вектора .

4. Из системы векторов: , , , , выделить базис и ортогонализовать его по процедуре Грамма-Шмидта:

g := [ a1, a2, a3, a5 ]

[[1,2,2, — 1], [2,3, — 3,2], ,

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Линал 2.6. Умножение матрицы на векторСкачать

5. Функции для работы, с векторами и матрицами

Функции для работы с векторами и матрицами

Для работы с векторами и матрицами Maple 7 имеет множество функций, входящих в пакет linalg. Ограничимся приведением краткого описания наиболее распространенных функций этой категории.

Операции со структурой отдельного вектора V и матрицы М:

coldim(M) — возвращает число столбцов матрицы М;
rowdim(M) — возвращает число строк матрицы М;
vectdim(V) — возвращает размерность вектора V;
col(M,i) — возвращает i-й столбец матрицы М;
row(M,i) — возвращает i-ю строку матрицы М;
tninor(M,i, j) — возвращает минор матрицы М для элемента с индексами i и j;
delcols(M,i.. j) — удаляет столбцы матрицы М от i-roдо j-ro;
del rows (V,i..j) — удаляет строки матрицы М от i-й до j-й;
extend (М, т, n,х) — расширяет матрицу М на m строк и n столбцов с применением заполнителя х.

Основные векторные и матричные операции:

dotprod(U,V) — возвращает скалярное произведение векторов U и V;
crossprod(U,V) — возвращает векторное произведение векторов U и V;
norm(V) или norm(M) — возвращает норму вектора или матрицы;
copyinto(A,B,i, j) — копирует матрицу А в В для элементов последовательно от i до j;
concat(Ml,M2) — возвращает объединенную матрицу с горизонтальным слиянием матриц Ml и М2;
stack(Ml,M2) — возвращает объединенную матрицу с вертикальным слиянием Ml и М2;
matadd(A,B) и evalm(A+B) — возвращает сумму матриц А и В;
multlply(A,B) и evalm(A&*B) — возвращает произведение матриц А и В;
adjoint (М) или adj(M) — возвращает присоединенную матрицу, такую что M?adj(M) дает диагональную матрицу, определитель которой есть det(M);
charpoly(M,lambda) — возвращает характеристический полином матрицы М относительно заданной переменной lambda;
det(M) — возвращает детерминант (определитель) матрицы М;
Eigenvals(M,vector) — инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) соответствующие им собственные векторы;
jordan(M) — возвращает матрицу М в форме Жордана;
hermite(M) — возвращает матрицу М в эрмитовой форме;
trace(M) — возвращает след матрицы М;
rank(M) — возвращает ранг матрицы М;
transpose(M) — возвращает транспонированную матрицу М;
inverse(M) или evalm(l/M) — возвращает матрицу, обратную к М;
singularvals(A) — возвращает сингулярные значения массива или матрицы А.

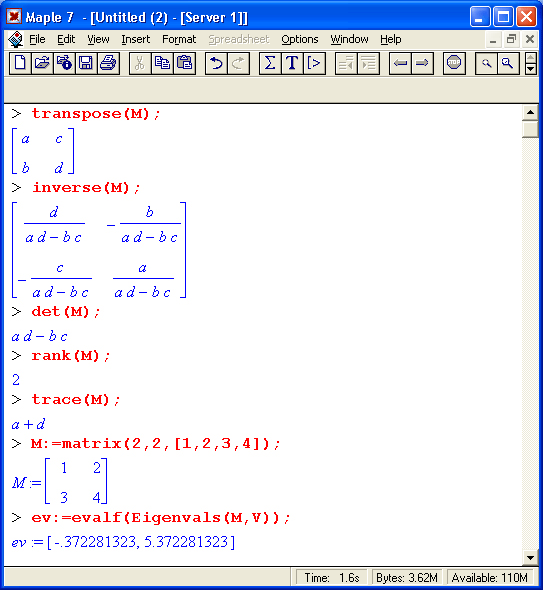
Приведем примеры применения некоторых из этих функций:

Читатель, понимающий суть матричных вычислений, легко справится с тестированием других функций, входящих в пакет linalg. В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.

Видео:Linear Algebra - Maple (Matrix Addition Subtraction Multiplication Inverse Determinant Transpose)Скачать

Линейная алгебра

Искусство использования матриц и векторов для решения задач физики

Видео:Занятие 12. Векторы и матрицыСкачать

Матрицы, векторы и основные операции с ними

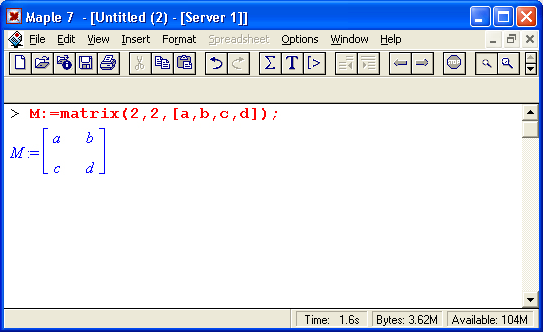
Прежде всего, надо знать, как создавать матрицы и векторы в Maple. Есть много способов, но рекомендуется близкий к тому, как это делает MatLab. Матрица A , содержащая 1, 2, 3, 4, получается так:

Для ссылок на элементы матрицы применяются обозначения вида A[row,column] , т. е.:

Если надо только определить матрицу B , но не присваивать ей значения, пишется:

Как только В определена, присвоить ей значения можно любым способом, в том числе и вручную:

Можно посмотреть на В , чтобы удостовериться в том, что все правильно:

Детали – см. справку, задав ?Matrix .

Можно создать векторы-столбцы или строки с помощью команды Vector :

По умолчанию создается вектор-столбец.

Для создания вектора-строки (row) надо сказать об этом Maple:

Если надо заполнить векторы числами из строк или столбцов матрицы – примените команды Column и Row . Например, чтобы заполнить с вторым столбцом матрицы А , надо написать:

Для заполнения с первой строкой А :

Вот еще удобный способ для определения матриц и векторов-столбцов без специальной команды, с помощью синтаксической конструкции ColumnRow :

А поскольку матрица представляется как набор векторов-столбцов, то её можно определить таким же способом:

Об этой форме представления надо знать, поскольку она часто используется в Maple help.

Определить матрицы в Maple можно с помощью MatrixPalette – палитры слева от рабочего листа. Использование элементов ее интерфейса очевидно, термины в основном понятны (на всякий случай: skewsymmetric – кососимметрическая). Установите курсор в пустую группу (лучше делать это на отдельном листе, как обычно) и выберите нужные опции в окне палитры. Можно вручную заполнить элементы матрицы m[x, x], можно использовать шаблон для матриц определенного вида. После этого она готова для присваивания с помощью := .

В Maple матрицы и векторы могут содержать и числа, и формулы:

Теперь предположим, что надо задать значения х и у и затем посмотреть на матрицы в представлении с плавающей запятой.

Уже было известно, что надо применить evalf :

Проблема в том, что е – это не выражение, а матрица выражений, поэтому Maple нужны две команды eval : evalm внутри, чтобы сослаться непосредственно на элементы е и evalf снаружи и запустить расчеты с плавающей запятой.

Спросите ?evalm , чтобы увидеть о чем эта команда, или

Запомните, что для получения численного ответа
надо применять десятичные точки в числах.

Функция evalm вычисляет выражения, включая матричные. Она выполняет суммирование, умножение, возведение в целую степень, в том числе для матриц, и показывает отображение функций на матрицы.

Учтите, что, прежде чем передавать аргументы в evalm , Maple может выполнить упрощения, которые будут действительны для матриц. Например, evalm(A^0) возвратит 1, а не единичную матрицу.

Неприсвоенные имена рассматриваются либо как символьные матрицы, либо как скаляры, в зависимости от их использования в выражении.

Для обозначения некоммутативного умножения матриц используйте оператор &* . Произведение матриц ABC может быть введено как A&*B&*C или как &*(A,B,C) , причем последнее более эффективно. Применяется автоматическое упрощение, такое как сбор констант и степеней. Не используйте * , чтобы обозначить чистое умножение матриц, поскольку это вернет ошибку. Операндами &* должны быть матрицы (или имена) за исключением 0. Невычисленное произведение матриц рассматривается как матрицы. Оператор &* имеет то же старшинство, что и оператор * .

Используйте 0, чтобы обозначить нулевой скаляр или матрицу. Применяйте &*() для обозначения единичной матрицы. Возможно, удобно применять alias(Id=&*()) .

Если в сумме есть матрица и константа, то Maple рассматривает константу как умноженную на единичную матрицу. Следовательно, матричные полиномы можно вводить в точности так, как скалярные полиномы.