Начертите окружность и постройте симметричную ей

О чем эта статья:

Видео:Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Осевая симметрия. 6 класс.Скачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Центральная симметрия. 6 класс.Скачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Как построить окружность симметричную ей

Видео:Осевая и центральная симметрия, 6 классСкачать

Урок 3. Окружность в перспективе. Как нарисовать кружку и вазу

В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк. Сложность их изображения в пространстве заключается в том, что принцип равноудаленности точек окружности от центра срабатывает, только когда мы смотрим на плоскость прямо (то есть направление взгляда перпендикулярно ей). Например, мы видим круглый циферблат часов перед собой или чашку и блюдце, когда наклонились над ними. В других случаях (взгляд падает на плоскость под углом) мы видим искажение формы окружности, ее превращение в овал (эллипс).

Содержание:

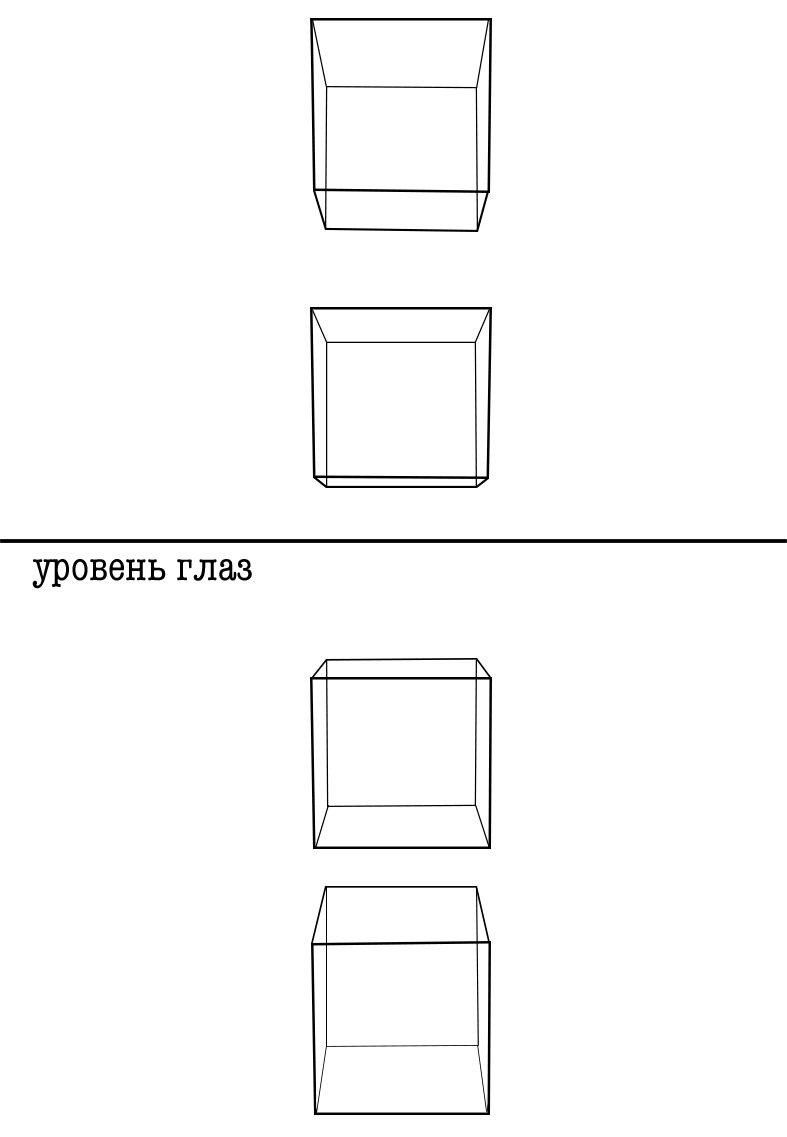
Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).

То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.

Видео:Ось симметрииСкачать

Принципы рисования эллипсов:

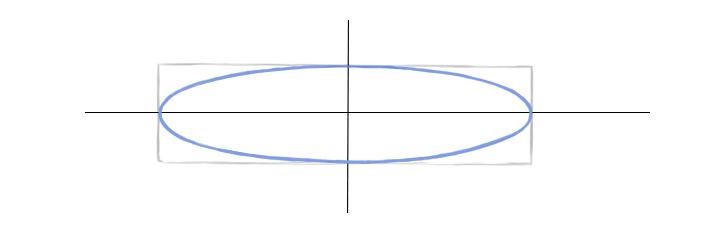
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.

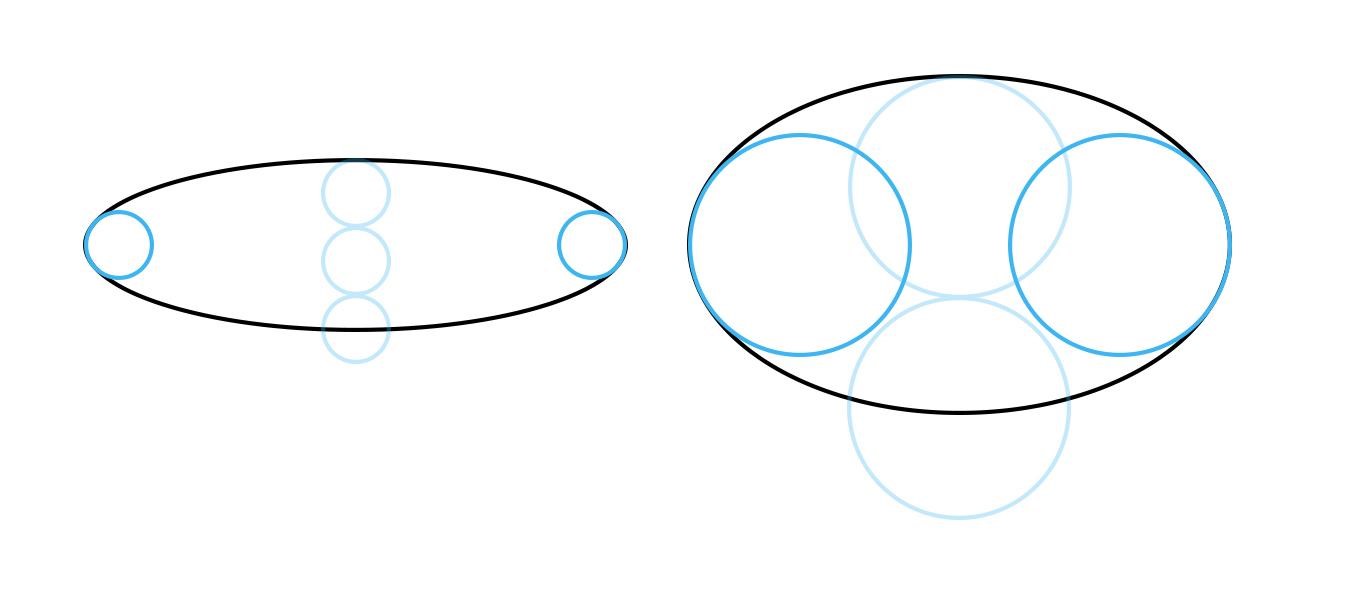
Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).

Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).

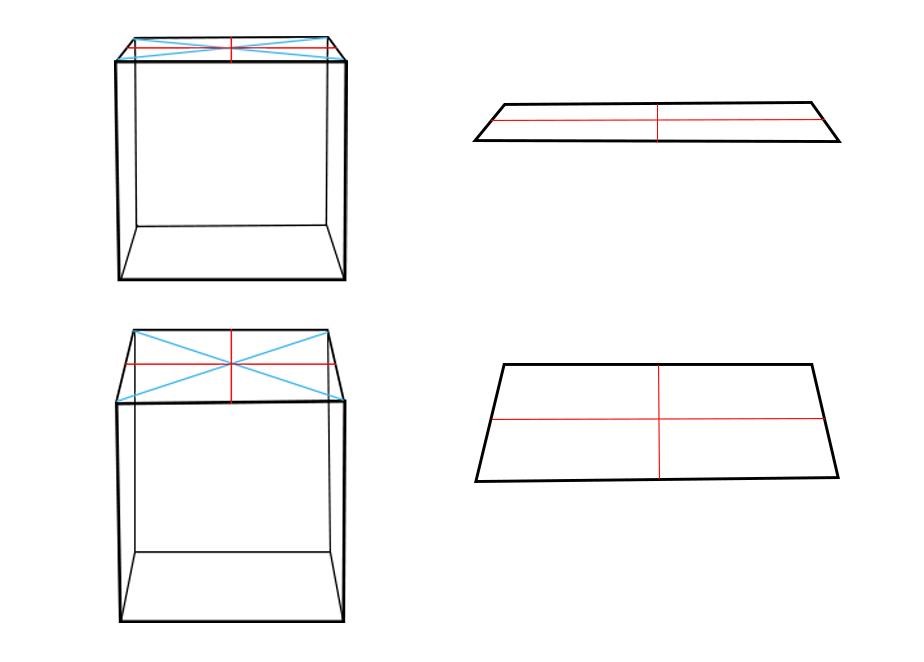
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

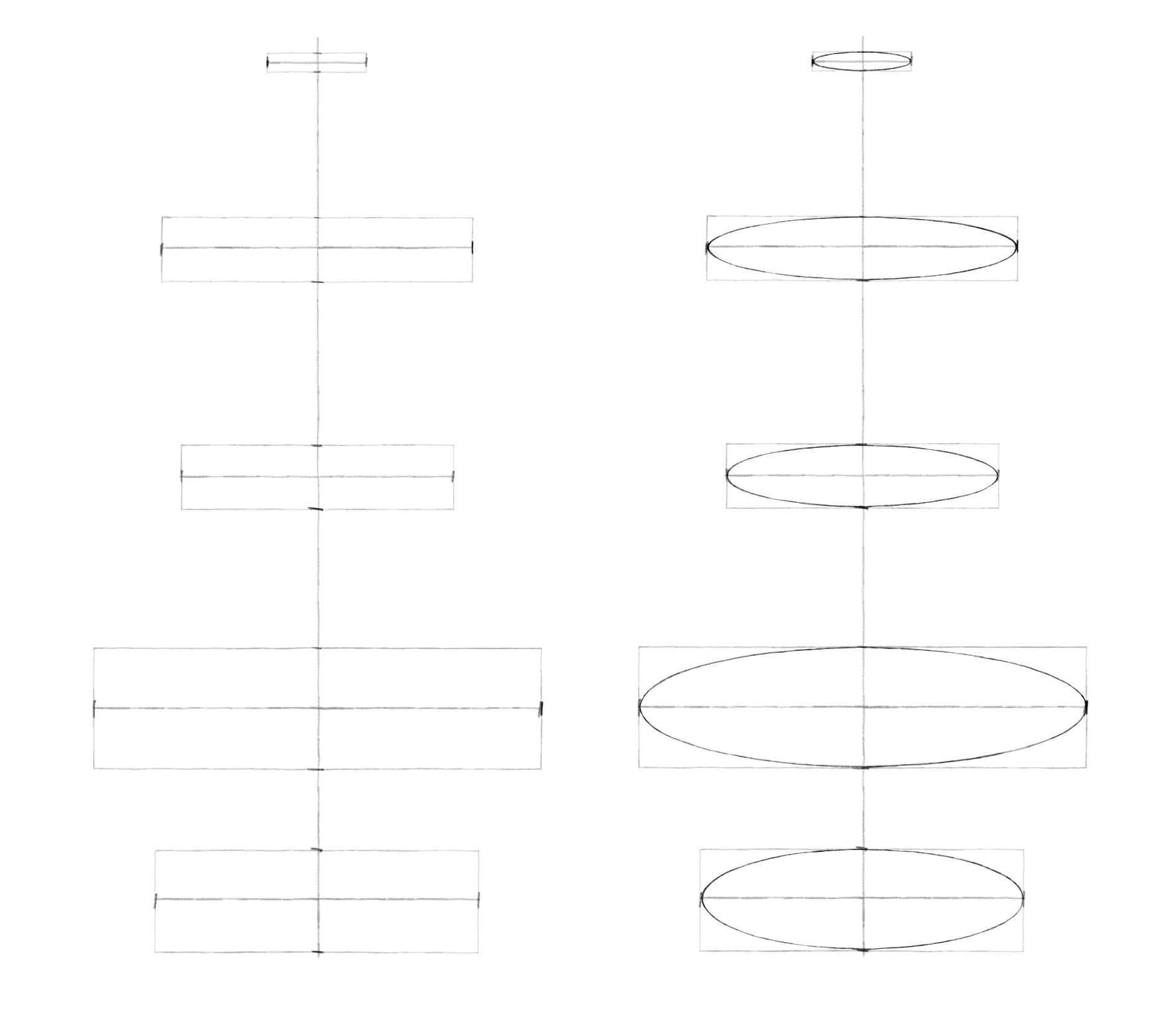
Рисуем эллипсы

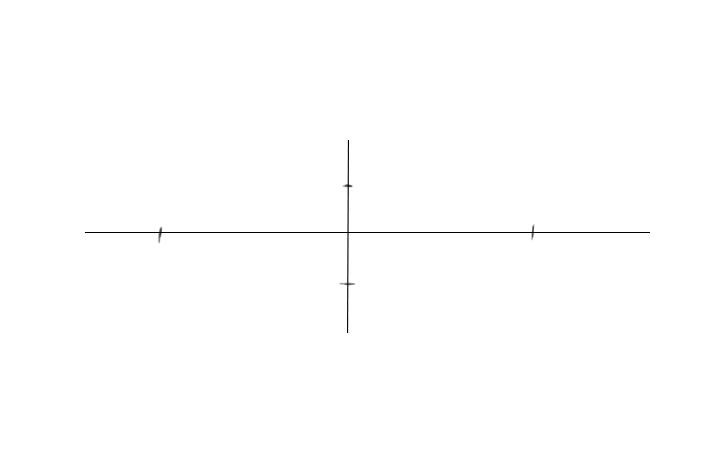
Шаг 1. Для начала проведем две перпендикулярных оси.

Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.

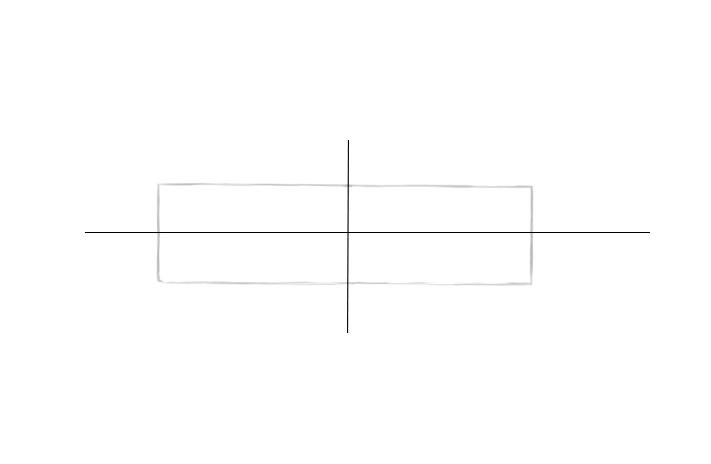
Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.

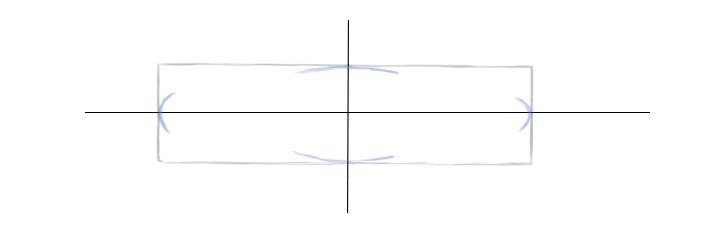
Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.

Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.

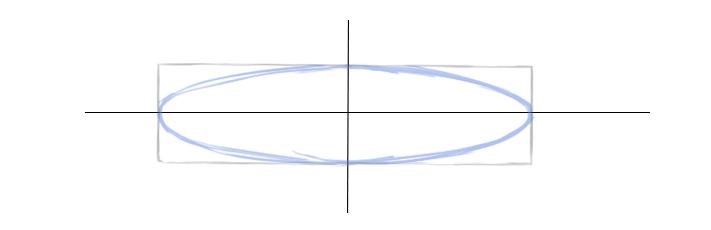
Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.

Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.

Видео:ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

Рисуем кружку

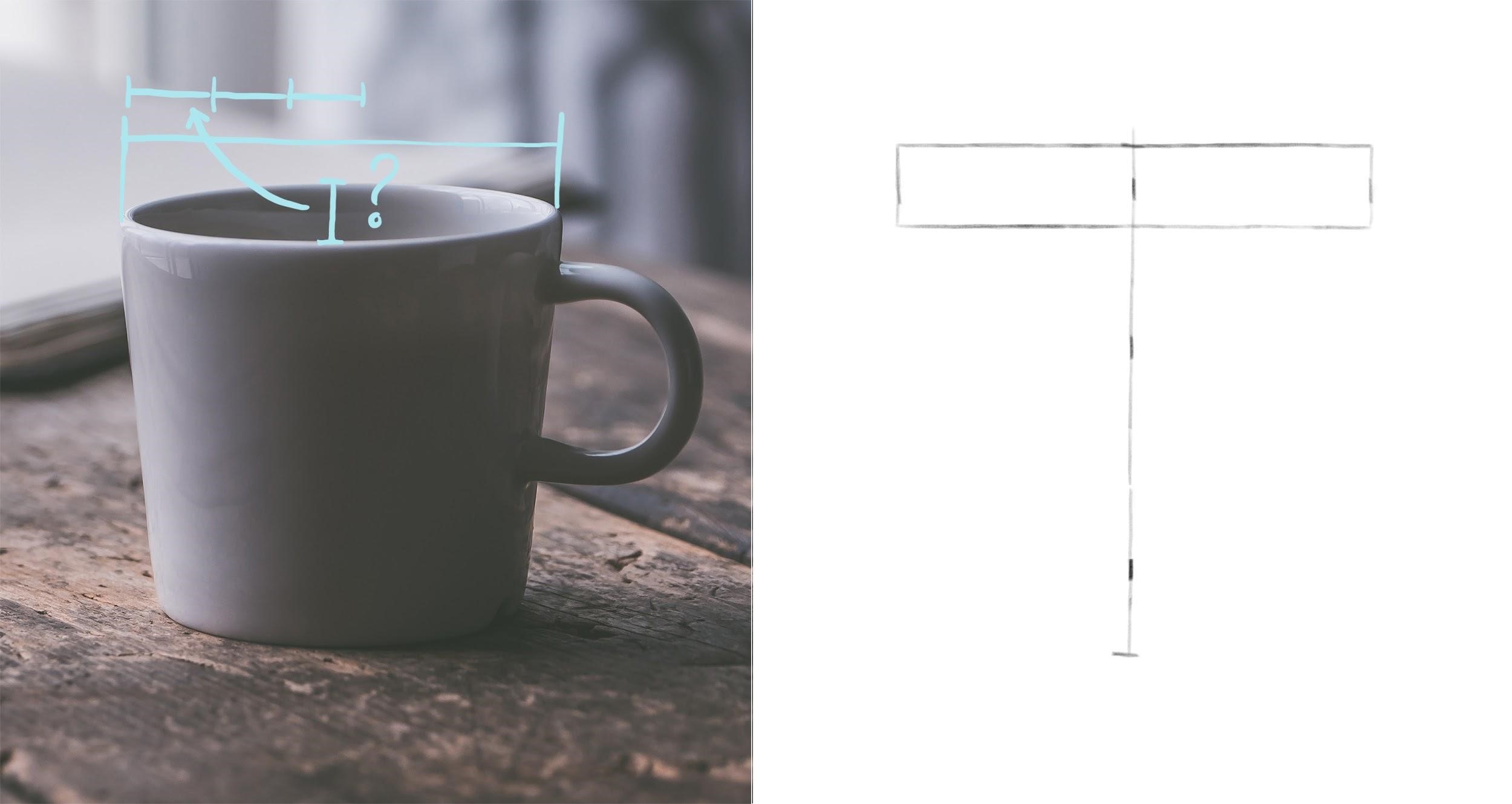
Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.

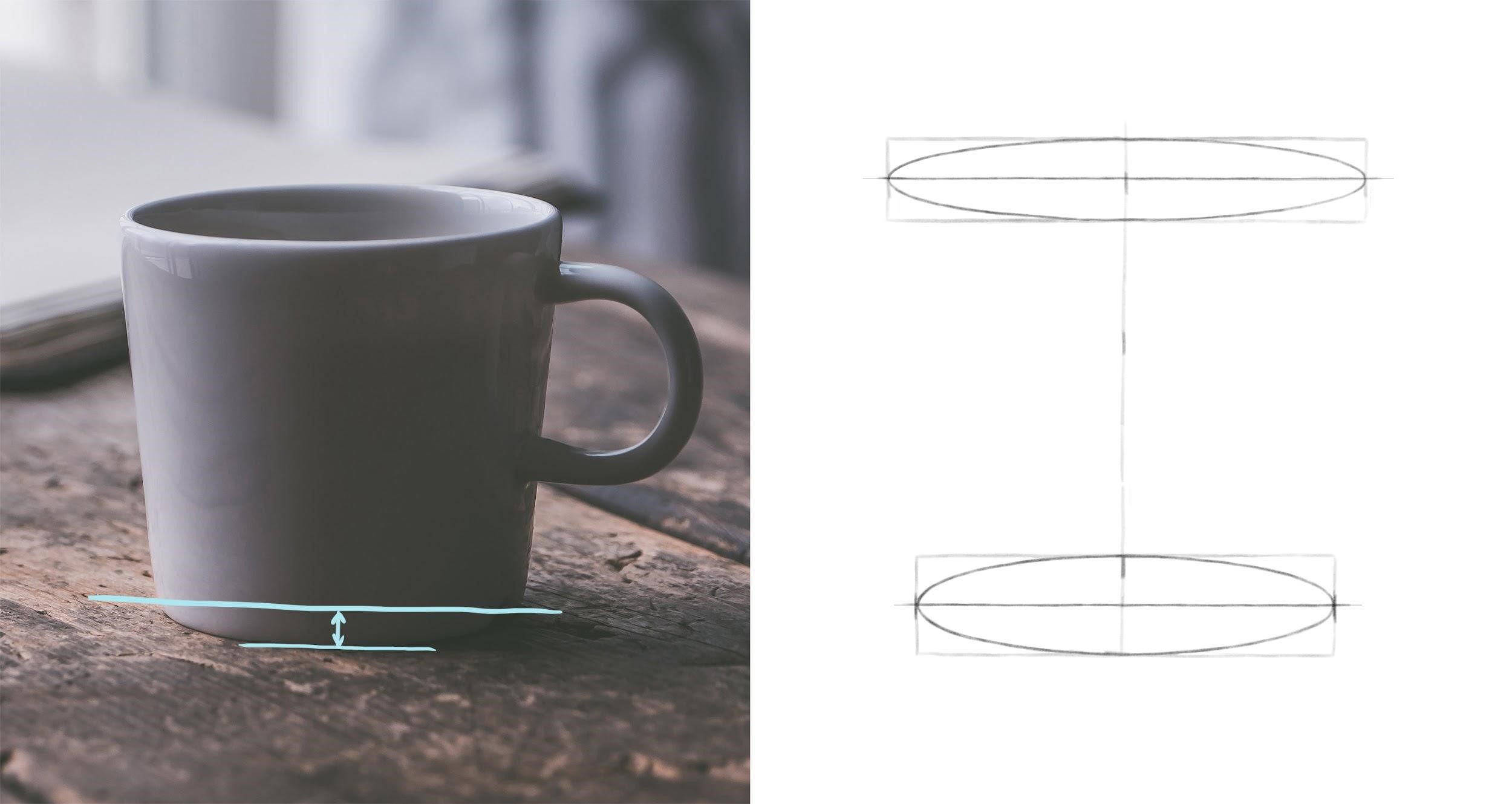
Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.

Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.

Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.

Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то — на глаз).

Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!

Видео:Построить описанную окружность (Задача 1)Скачать

Рисуем вазу

В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.

В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).

Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.

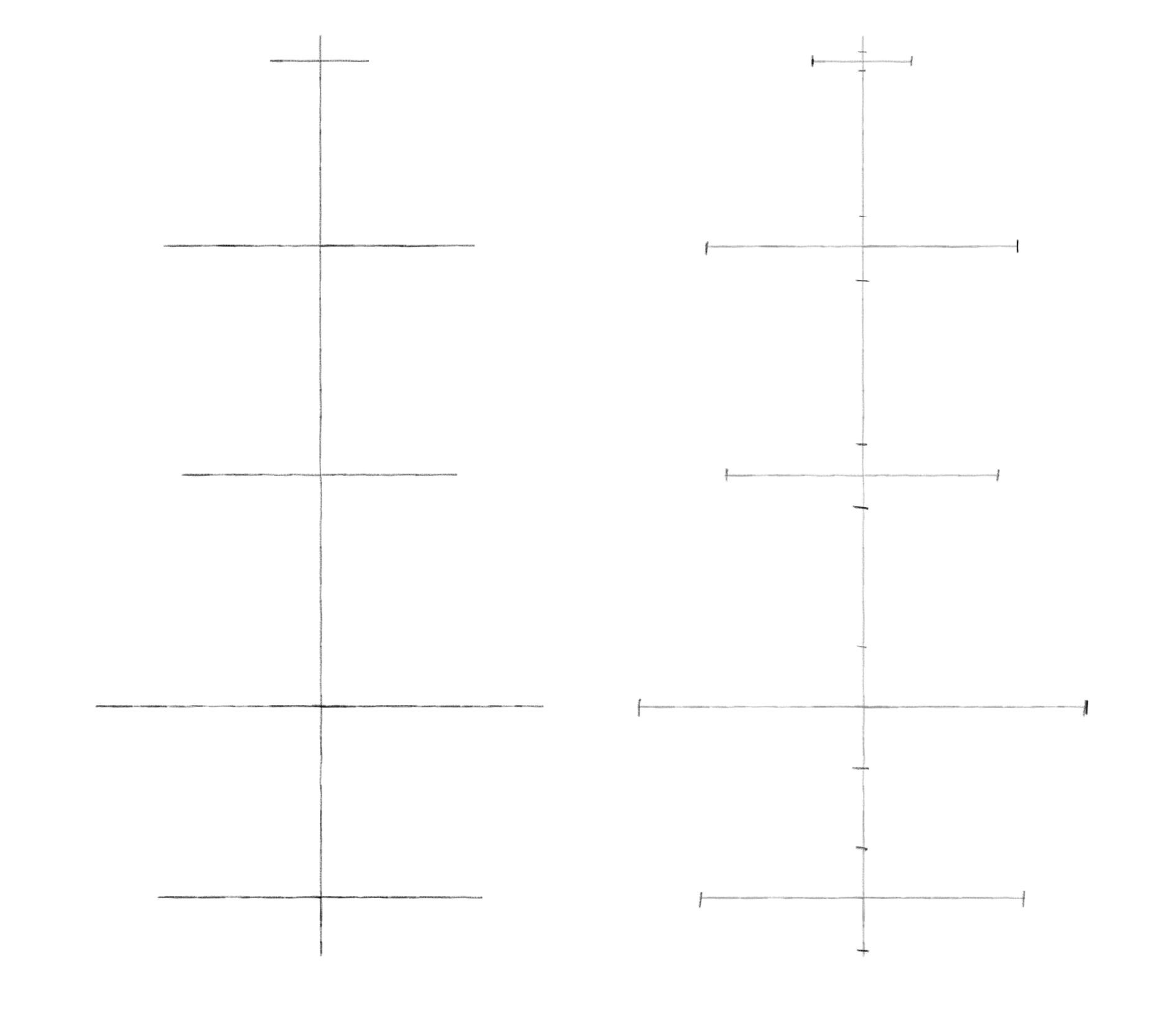
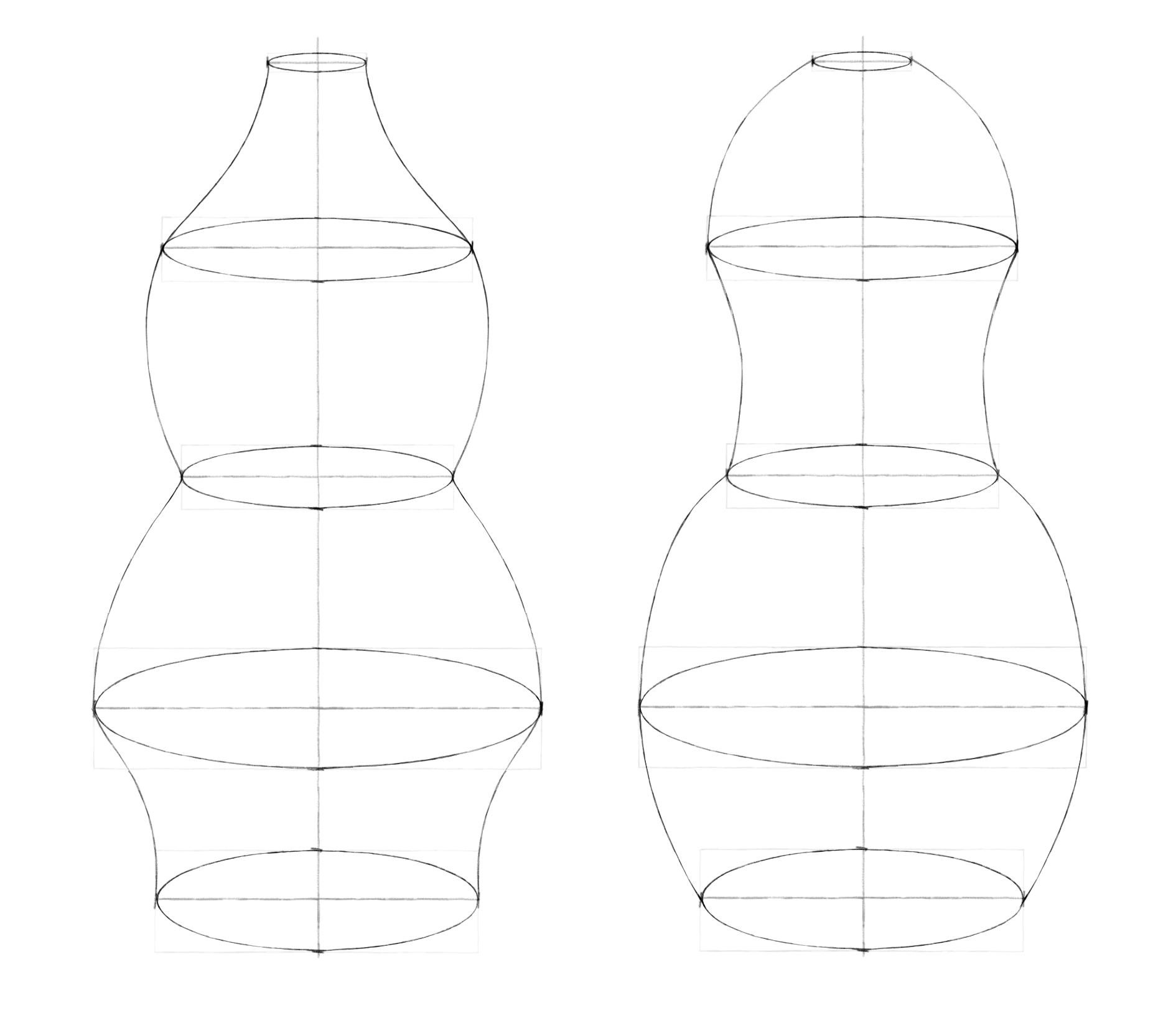
Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.

Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).

Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.

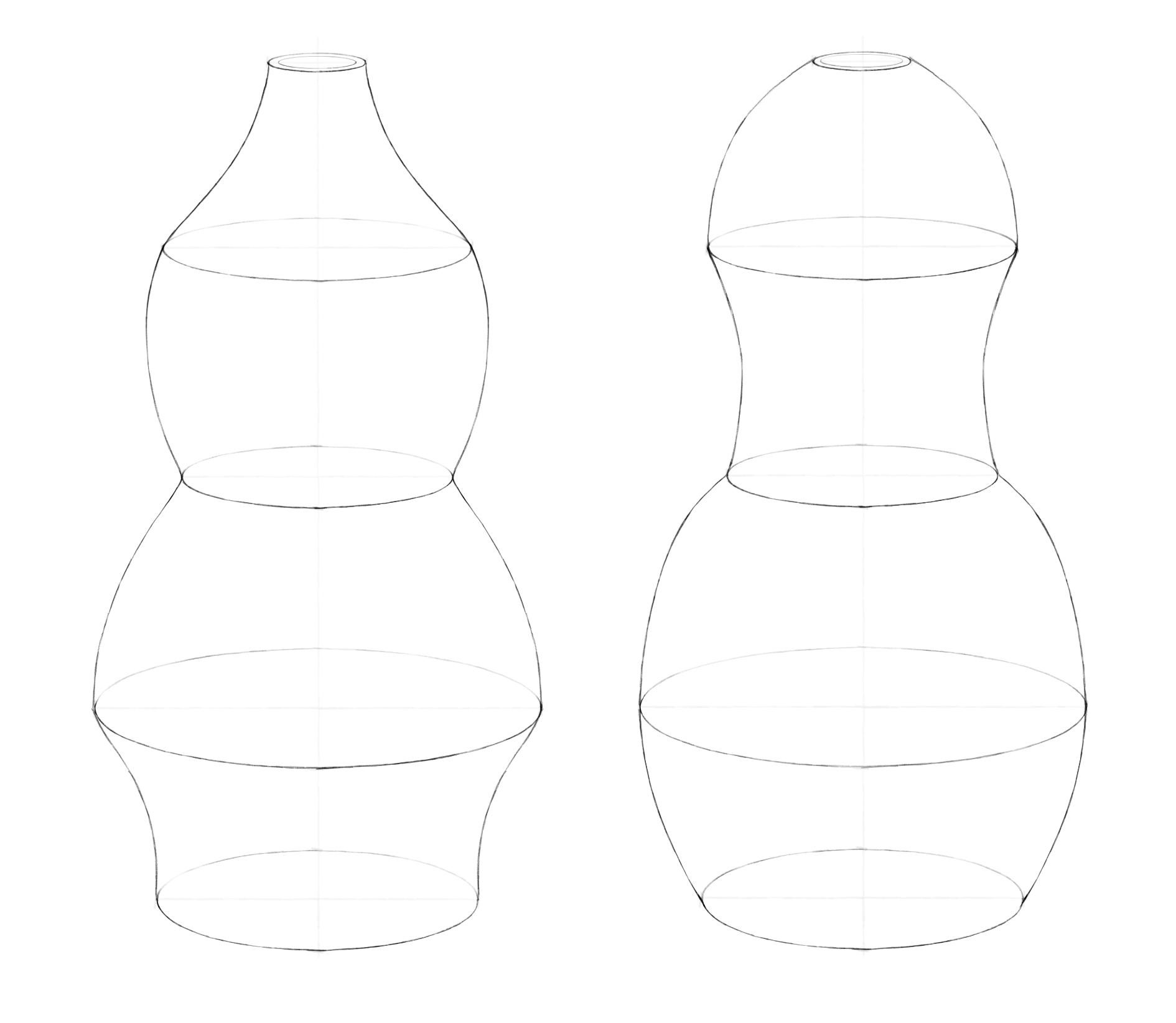
Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.

Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!

Видео:6 класс, 26 урок, СимметрияСкачать

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Осевая и центральная симметрия

О чем эта статья:

Видео:Тригонометрическая окружность. Как выучить?Скачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Окружность. Круг. 5 класс.Скачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Уравнение окружности (1)Скачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Начертите окружность и постройте симметричную ей окружность относительно прямой, которая: а) не пересекает окружность;

Видео:Центральная и осевая симметрии. Геометрия 7 класс.Скачать

Ваш ответ

Видео:Осевая и центральная симметрии. 6 класс.Скачать

решение вопроса

Видео:№150. Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окр-тиСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,857
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Дидактические материалы по математике на тему «Симметрия» (6 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Задание № 3 Свойства симметричных фигур.docx

Задание № 3 «Свойства симметричных фигур»

1º. При симметрии точки переходят в точки, отрезки — в отрезки, прямые — в прямые, многоугольники, переходят в равные данным многоугольникам.

2º. Симметрия сохраняет расстояние между точками.

3º. Любая прямая, проходящая через центр симметрии, делит её на две равные фигуры.

1

3

4 Нарисуйте фигуру, которая получится, если повернуть фигуру С на 90° против часовой стрелки относительно точки M.

5 На рисунке 1 показаны фигуры, симметричные относительно точки О. На рисунке 2 показаны фигура и точка О. Нарисуйте фигуру, симметричную данной относительно точки О.

6 Разрежьте квадрат на две равные по площади фигуры шестью разными способами

Выбранный для просмотра документ Задание № 1 Симметрия и её разнообразие..docx

Задание № 1 «Симметрия и её разнообразие».

1. Постройте отрезок . Постройте отрезок , симметричный относительно точки, не лежащей на данном отрезке.

2. Постройте отрезок , симметричный относительно прямой.

3. Постройте равнобедренный треугольник, основание которого равно 2 см, а высота равна 3 см. Изобразите треугольник , симметричный данному треугольнику относительно :

а) точки б) прямой

3. Дан прямоугольник со сторонами 1 см и 4 см. Постройте фигуру, симметричную относительно точки.

4. Изобразите ось симметрии у прямоугольника, квадрата , круга, ромба и равнобедренного треугольника. Определите количество осей симметрии.

5. Приведите примеры ассиметричных фигур.

6. Назовите буквы русского алфавита, имеющие одну ось симметрии? две оси симметрии?

7. Постройте квадрат со стороной 2 см. Изобразите фигуру , симметричную квадрату относительно точки, лежащей вне плоскости квадрата. Сравните площади двух фигур.

8. Постройте трапецию. Изобразите фигуру , симметричную относительно прямой , не пересекающей плоскость трапеции.

9. Постройте фигуру, у которой имеется центр и ось симметрии

10. Постройте фигуру, у которой имеется ось симметрии, но не имеет центра симметрии.

Выбранный для просмотра документ Задание № 2 Построение равных фигур.docx

Задание № 2 «Построение равных фигур»

1. Начертите отрезок АВ. Отметьте точку О, не лежащую на отрезке АВ. Постройте отрезок, симметричный отрезку АВ относительно точки О.

Чертёжник чертил деталь, но начертил только половину. Начертите вторую половину детали симметрично относительно пунктирной прямой

3. Нарисуйте фигуру, симметричную заштрихованной фигуре относительно данной прямой.

4. Постройте отрезок, симметричный отрезку АВ относительно прямой а, а затем отрезок, симметричный получившемуся относительно прямой к.

5. Достройте фигуру, используя симметричность относительно прямой:

6. Постройте фигуру, симметричную данной, относительно центра – точки О

Выбранный для просмотра документ Зачёт № 3 Симметрия.docx

Зачёт № 3 по теме «Симметрия»

1. Построить отрезок. Назовите его. Постройте отрезок, симметричный данному отрезку относительно точки, не лежащей отрезке.

2. Построить равнобедренный треугольник. Назовите его. Постройте треугольник, симметричный данному треугольнику относительно прямой, не лежащей в плоскости данного треугольника.

3. Построить трапецию. Назовите её. Постройте её отображение относительно точки, не лежащей в плоскости заданной трапеции.

4. Изобразить прямоугольник со сторонами 3 см и 4 см. Постройте отображение данного прямоугольника путём поворота по часовой стрелке на 90º относительно точки , не лежащей в плоскости прямоугольника.

5. Задайте фигуру площадью 3 кв. ед. Постройте равносоставленную комбинированную фигуру . Найдите её площадь. Изобразите её отображение относительно прямой .

Зачёт № 3 по теме «Симметрия»

1. Построить отрезок. Назовите его. Постройте отрезок , симметричный данному отрезку относительно прямой, не лежащей на данном отрезке.

2. Построить прямоугольный треугольник. Назовите его . Постройте его отображение относительно точки , не лежащей в плоскости данного треугольника.

3. Построить равнобедренную трапецию. Назовите её. Постройте трапецию, симметричную данной трапеции относительно прямой, не лежащей в плоскости данной трапеции.

4. Изобразить прямоугольник со сторонами 2 см и 3 см. Постройте отображение данного прямоугольника путём поворота по часовой стрелке на 90º относительно точки , не лежащей в плоскости прямоугольника.

5. Приведите примеры фигур:

а) у которой одна ось симметрии, проиллюстрируйте свой выбор;

б) у которой две оси симметрии, постройте оси симметрий;

в) у которой нет оси симметрии.

Зачёт № 3 по теме «Симметрия»

1. Построить отрезок. Назовите его. Постройте его отображение , относительно прямой, не лежащей на данном отрезке.

2. Построить тупоугольный треугольник. Назовите его. Постройте треугольник симметричный данному относительно точки , не лежащей в плоскости данного треугольника.

3. Построить круг радиусом 2 см. Построить круг, симметричный данному относительно прямой, пересекающей данный круг.

4. Задайте фигуру площадью 5 кв. ед. Постройте равносоставленную комбинированную фигуру . Найдите её площадь. Изобразите её отображение относительно прямой .

5. Приведите примеры фигур:

а) у которой одна ось симметрии, проиллюстрируйте свой выбор;

б) у которой две оси симметрии, проиллюстрируйте свой выбор;

в) у которой нет оси симметрии.

Зачёт № 3 по теме «Симметрия»

1. Построить отрезок. Назовите его. Постройте его отображение, симметричное относительно точки , не лежащей на данном отрезке.

2. Построить прямоугольный треугольник. Назовите его. Постройте его отображение относительно прямой, не лежащей в плоскости данного треугольника.

3. Изобразить прямоугольник со сторонами 2 см и 4 см. Постройте отображение данного прямоугольника путём поворота по часовой стрелке на 90º относительно точки , не лежащей в плоскости прямоугольника.

4. Задайте фигуру площадью 3 кв. ед. Постройте равносоставленную комбинированную фигуру . Найдите её площадь. Изобразите её отображение относительно прямой .

5. Приведите примеры фигур:

а) у которой одна ось симметрии, проиллюстрируйте свой выбор;

б) у которой две оси симметрии, проиллюстрируйте свой выбор;

в) у которой нет оси симметрии.

Зачёт № 3 по теме «Симметрия»

1. Построить отрезок . Назовите его. Постройте отрезок , симметричный данному относительно прямой, не лежащей на данном отрезке.

2. Построить круг радиусом 2 см. Отобразите круг относительно прямой, не пересекающей данный круг.

3. Построить равнобедренную трапецию. Назовите её. Постройте её отображение относительно точки, не лежащей в плоскости данной трапеции.

4. Изобразить прямоугольник со сторонами 3 см и 4 см. Постройте отображение данного прямоугольника путём поворота против часовой стрелки на 90º относительно точки , не лежащей в плоскости прямоугольника.

5. Приведите примеры фигур:

а) у которой одна ось симметрии, проиллюстрируйте свой выбор;

б) у которой две оси симметрии, проиллюстрируйте свой выбор;

в) у которой нет оси симметрии.

Зачёт № 3 по теме «Симметрия»

1. Построить отрезок. Назовите его. Постройте отрезок симметричный данному относительно точки , не лежащей на данном отрезке.

2. Построить правильный треугольник со стороной 2 см. Назовите его. Постройте его отображение относительно прямой, не лежащей в плоскости данного треугольника.

3. Изобразить прямоугольник со сторонами 1 см и 3 см. Постройте отображение данного прямоугольника путём поворота против часовой стрелки на 90º относительно точки , не лежащей в плоскости прямоугольника.

4. Задайте фигуру площадью 4 кв. ед. Постройте равносоставленную комбинированную фигуру . Найдите её площадь. Изобразите её отображение относительно прямой .

5. Приведите примеры фигур:

а) у которой одна ось симметрии, проиллюстрируйте свой выбор;

б) у которой две оси симметрии, проиллюстрируйте свой выбор;

в) у которой нет оси симметрии.

Зачёт № 3 по теме «Симметрия»

1. Построить отрезок. Назовите его. Постройте его отображение симметрично относительно прямой, не лежащей на данном отрезке.

2. Построить равнобедренную трапецию. Назовите её. Постройте трапецию, симметричную данной относительно точки , не лежащей в плоскости данной трапеции.

3. Изобразить прямоугольник со сторонами 1 см и 4 см. Постройте отображение данного прямоугольника путём поворота по часовой стрелке на 90º относительно точки , не лежащей в плоскости прямоугольника.

4. Задайте фигуру площадью 3 кв. ед. Постройте равносоставленную комбинированную фигуру . Найдите её площадь. Изобразите её отображение относительно прямой .

5. Приведите примеры фигур:

а) у которой бесконечно много осей симметрии, проиллюстрируйте свой выбор;

б) у которой две оси симметрии, проиллюстрируйте свой выбор ;

в) у которой нет оси симметрии.

Выбранный для просмотра документ Обобщающее занятие по теме Симметрия.docx

Обобщающее занятие по теме «Симметрия»

1. Построить отрезок и отобразить его симметрично относительно точки ( прямой), не лежащей на данном отрезке.

2. Построить прямоугольный треугольник и отобразить его относительно точки (прямой), не лежащей в плоскости данного треугольника.

3. Построить равнобедренную трапецию и отобразить её относительно точки(прямой), не лежащей в плоскости данной трапеции.

4. Изобразить прямоугольник со сторонами 2 см и 3 см. Постройте отображение данного прямоугольника путём поворота по часовой стрелке на 90º относительно точки , не лежащей в плоскости прямоугольника.

5. Задайте фигуру площадью 4 кв. ед. Постройте равносоставленную комбинированную фигуру . Найдите её площадь. Изобразите её отображение относительно прямой .

6. Приведите примеры фигур:

а) у которой одна ось симметрии;

б) у которой две оси симметрии;

в) у которой нет оси симметрии.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 934 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 312 человек из 67 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 688 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 491 192 материала в базе

Материал подходит для УМК

«Математика», Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др. / Под ред. Дорофеева Г.В., Шарыгина И.Ф.

Глава 7. Симметрия

Дистанционные курсы для педагогов

Другие материалы

• 27.03.2021
• 258

• 27.03.2021
• 55

• 27.03.2021
• 1036

• 27.03.2021
• 80

• 27.03.2021
• 200

• 27.03.2021
• 123

• 27.03.2021
• 65

• 27.03.2021
• 91

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 27.03.2021 1177 —> —> —> —>
• ZIP 381.4 кбайт —> —>
• Рейтинг: 2 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Нефёдова Оксана Алексеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 11 месяцев
• Подписчики: 0
• Всего просмотров: 7049
• Всего материалов: 16

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Школы Сургута переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Минспорта утвердило программу подготовки киберспортсменов

Время чтения: 1 минута

«Учителя года» проведут открытые занятия для педагогов России

Время чтения: 1 минута

Свободное движение повышает креативность

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.