Отношение сторон треугольника при биссектрисе

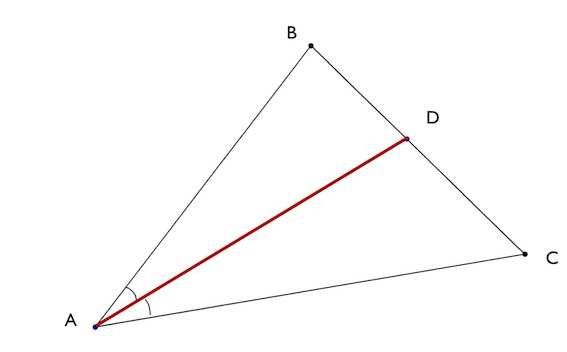
Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:

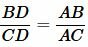(1)

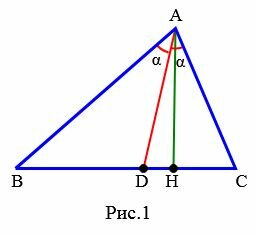Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:

,

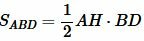(3)

.

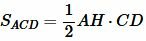(4)

Построим следующее соотношение

.

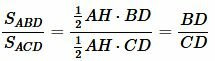(5)

С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:

.

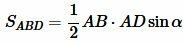(6)

.

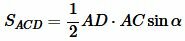(7)

Построим следующее соотношение используя формулы (6) и (7):

.

(8)

Из формул (5) и (8) получим соотношение (1).

Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).

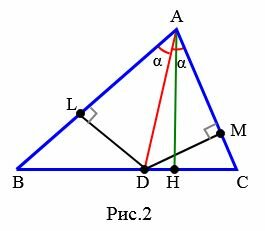Тогда площади треугольников ABD и ACD можно найти из формул:

,

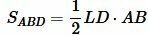(9)

.

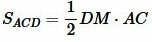(10)

Построим следующее соотношение

.

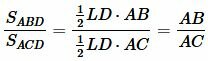(11)

Из формул (5) и (11) получим соотношение (1).

Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):

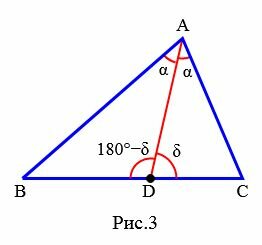Применяя теорему синусов для треугольников ABD и ACD можем записать:

,

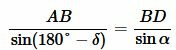(12)

.

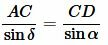(13)

Поделив (12) на (13) и учитывая, что ( small sin(180°-delta)=sin delta , ) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).

Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.

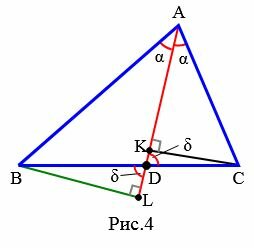Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (( small ∠ ALB= ∠ AKC ,;; ∠ BAL= ∠ CAK ) ). Тогда имеем:

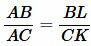(14)

Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку ( small ∠ BLD= ∠ CKD ,) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:

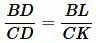(15)

Из равенств (14) и (15) получаем:

.

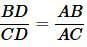Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.

Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:

.

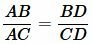(16)

Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:

.

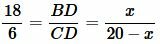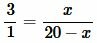(17)

Методом перекресного умножения упростим (17) и решим:

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:Построение биссектрисы углаСкачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Видео:8 класс, 35 урок, Свойства биссектрисы углаСкачать

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Видео:Формула для биссектрисы треугольникаСкачать

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Видео:Свойства биссектрисы треугольникаСкачать

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

📽️ Видео

3 свойства биссектрисы #shortsСкачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Свойство биссектрисы внешнего угла треугольникаСкачать

Задание 26 Отношение площадей Свойство биссектрисыСкачать

Cекретное свойство биссектрисыСкачать

Свойства биссектрисыСкачать

Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

СВОЙСТВО БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Свойство биссектрисы треугольникаСкачать

ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Найдите биссектрису треугольникаСкачать

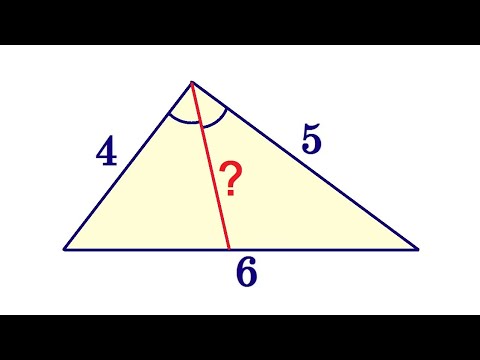
Свойство биссектрисы треугольникаСкачать