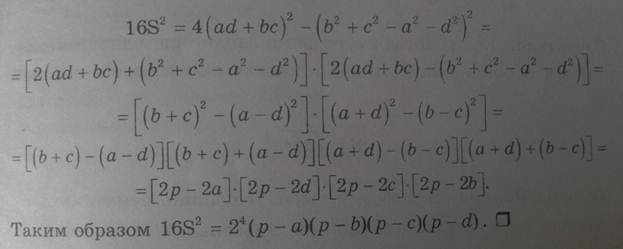Класс: 8
- Презентация к уроку
- Ход урока
- Введение
- 1. Теоретическая часть
- 2. Практическая часть. Решение задач.
- Заключение
- Четырехугольники
- теория по математике 📈 планиметрия
- Выпуклый четырехугольник
- Виды и свойства выпуклых четырехугольников
- Прямоугольник
- Квадрат
- Параллелограмм
- Трапеция
- Виды трапеций
- Средняя линия трапеции
- Лемма о воздушном змее диагонали разбивают четырехугольник
- 🔍 Видео
Презентация к уроку
Загрузить презентацию (276 кБ)
Цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Задачи:
- Изучить теоретический материал: понятия «параллелограмм Вариньона», бимедианы четырехугольника, разобрать доказательство теоремы Вариньона и следствия из нее.
- Сравнить количество времени, необходимое для решения задач традиционным способом и, используя теорему Вариньона.
- Показать решение олимпиадных заданий с помощью параллелограмма Вариньона.
Видео:МЫ ЗАПУСТИЛИ ВОЗДУШНОГО ЗМЕЯ НА ОЧЕНЬ БОЛЬШУЮ ВЫСОТУСкачать

Ход урока
Введение
В 21 век, в век информационных технологий, главным ресурсом является время. Тысячи людей желают посещать тренинги, семинары и лекции по тайм-менеджменту, где бы их научили, как рационально, с минимальными потерями и максимальной пользой использовать свое время. Большую часть времени у ученика занимает обучение в школе и приготовление домашнего задания. Одним из самых сложных предметов в школе является геометрия. В частности, задачи на доказательство требуют значительной траты времени, поэтому у многих отсутствует интерес к решению подобных заданий. В теме «Четырехугольники» эту проблему может решить использование теоремы Вариньона.
Пьер Вариньон – французский математик и механик 18 века, который первым доказал, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма. Эта теорема вызвала интерес у отечественных ученых лишь в 20 веке. Подробно ее применение показал украинский геометр – Г.Б.Филипповский и кандидат физико-математических наук, доцент МГУ В.В. Вавилов. В школе теорема Вариньона не входит в курс программы, но считаю изучение её необходимым.
1. Теоретическая часть
Вариньон Пьер [1] (1654–1722)
Пьер Вариньон родился во Франции в 1654 году. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году. Вариньон готовился к религиозной деятельности, но, изучая сочинения Эвклида и Декарта, увлекся математикой и механикой. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике и физике. Вариньон был одним из первых ученых, ознакомивших Францию с анализом бесконечно малых. В конце 17 и начале 18 в. Вариньон руководил «Журналом ученых», в котором помещали свои работы по исчислению бесконечно малых братья Бернулли. В геометрии Вариньон изучал различные специальные кривые, в частности ввел термин «логарифмическая спираль». Главные заслуги Вариньона относятся к теоретической механике, а именно к геометрической статике. В 1687 Вариньон представил в Парижскую АН сочинение «Проект новой механики. », в котором сформулировал закон параллелограмма сил. В 1725 в Париже был издан трактат Вариньона «Новая механика или статика», представляющий собой систематическое изложение учения о сложении и разложении сил, о моментах сил и правилах оперирования ими, почти без изменений сохранившееся в учебниках статики до нашего времени. Написал учебник по элементарной геометрии (издан в 1731).
Теорема Вариньона [2]
Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.
 |
 |
 |
 |
 |
 |
 |
 |
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Совершившая неожиданный полет на воздушном змее девочка отделалась испугомСкачать

Лемма о воздушном змее диагонали разбивают четырехугольник
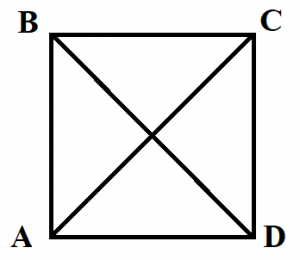
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла. Четырехугольник, у которого угол больше развернутого называется невыпуклым
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
- Сумма углов четырёхугольника равна 2 π = 360°.
- Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
- Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
- Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Теорема Вариньона
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство
Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников 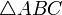
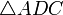
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ 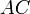
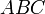
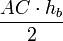
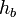
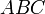
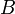
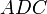
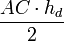
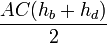
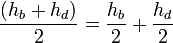
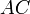
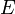
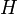
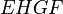
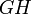
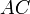
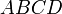
Теорема Эйлера
в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями
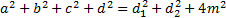

Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон
Теорема Птолемея
Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)
Если a, b, c, d – длины сторон четырёхугольника, 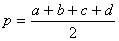
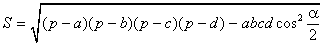
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: 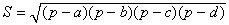
это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: 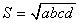
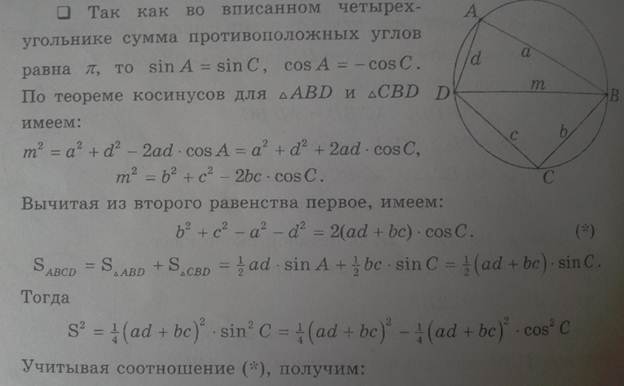
🔍 Видео
Воздушные змеи это весело говорили ониСкачать

Площади | Задачи 17-27 | Решение задач | Волчкевич | Уроки геометрии 7-8 классыСкачать

Чуть не улетел на гигантском воздушном змее в стратосферы!)Скачать

как запустить и собрать воздушного змеяСкачать

Галилео. Воздушный змей 🎐 KiteСкачать

На фестивале воздушных змеев девочка зацепилась за хвост и взлетела #shorts #новостиСкачать

МЫ ЗАПУСТИЛИ ВОЗДУШНОГО ЗМЕЯ НА ОЧЕНЬ БОЛЬШУЮ ВЫСОТУ | РЕАКЦИЯ на SlivkiShowСкачать

Запуск воздушного змея с ретрансляторомСкачать

Не ожидал что его унесет на воздушном змееСкачать

Огромные воздушные змеи 😱😳Скачать

Девушка зацепилась за воздушного змеяСкачать

в Китае прошел международный фестиваль воздушных змеевСкачать

Девочку унесло в небо на воздушном змее! #ShortsСкачать

Видеокамера на воздушном змее, как сделать, и аэросьемка!Скачать

Как запустить воздушного змеяСкачать

Грандиозный фестиваль воздушных змеев в КитаеСкачать




 Определение
Определение

 На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь
На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь 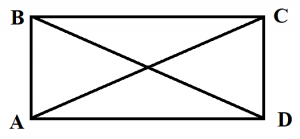
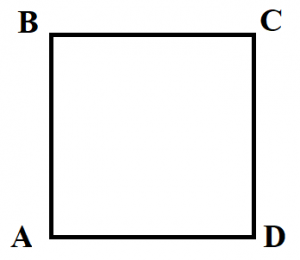 Свойства квадрата
Свойства квадрата