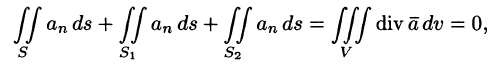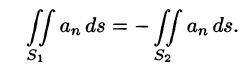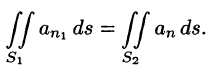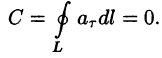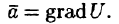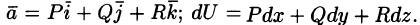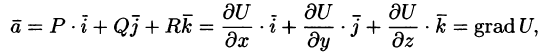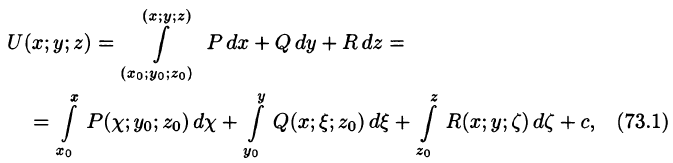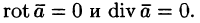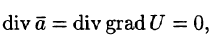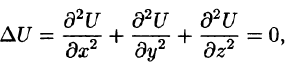Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
рассмотрели три основные операции векторного анализа: вычисление gradtx для скалярного поля а и rot а для векторного поля а = а(ж, у, г). Эти операции могут быть записаны в более простом виде с помощью символического оператора V («набла»): Оператор V (оператор Гамильтона) обладает как дифференциальными, так и вектор- ными свойствами.
Формальное умножение, например, умножение ^ на функцию и(х, у), будем понимать как частное дифференцирование: В рамках векторной алгебры формальные операции над оператором V будем проводить так, как если бы он был вектором. Используя этот формализм, получим следующие основные формулы: 1.
Если — скалярная дифференцируемая функция, то по правилу умножения вектора на скаляр получим где P, Q, R — дифференцируемые функции, то по формуле для нахождения скалярного произведения получим Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 3.
Вычисляя векторное произведение [V, а], получим Для постоянной функции и = с получим а для постоянного вектора с будем иметь Из распределительного свойства для скалярного и векторного произведений получаем Замечание 1. Формулы (5) и (6) можно трактовать тамке как проявление дифференциальных свойств оператора «набла» (V — линейный дифференциальный оператор). Условились считал., что оператор V действует на все величины, написанные за ним.
В этом смысле, например, — скалярный дифференциальный оператор.
Применяя оператор V к произведению каких-либо величин, надо иметь в виду обычное правило дифференцирования произведения. Пример 1. Доказать, что По формуле (2) с учетом замечания 1 получаем или Чтобы отметить тот факт, что «набл а» не действует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом с («const»), который в окончательном результате опускается. Пример 2.
Пусть u(xty,z) — скалярная дифференцируемая функция, а(х,у,г) — векторная дифференцируемая функция. Доказать, что 4 Перепишем левую часть (8) в символическом виде Учитывая дифференциальный характер оператора V, получаем . Так как ие — постоянный скаляр, то его можно вынести за знак скалярного произведения, так что а (на последнем шаге мы опустили индекс е). В выражении (V, иас) оператор V действует только на скалярную функцию и, поэтому В итоге получаем Замечай ие 2.
Используя формализм действа с оператором V как с вектором, надо помнить, что V не является обычным вектором — он не им«ет ни длины, ни направления, так что. например, вектор [V,aJ не будет, вообще говоря, перпендикулярным вектору а (впрочем, для плоского поля вектор перпендикулярен плоскости ,а значит, и вектору а).
Возможно вам будут полезны данные страницы:
Не имеет смысла и понятие коллинеарности по отношению к символическому вектору V. Например, выражение , где V и ^ — скалярные функции, формально напоминает векторное произведение двух коллинеарных векторов, которое всегда равно нулю. Однако вобшем случае это не имеет места. В самом деле, вектор = grad направлен по нормали к поверхности уровня , а вектор Vy = grad t> определяет нормаль к поверхности уровня i> = const.
| Вобшем случае эти нормали не обязаны |
быть коллннеарнымн (рис. 40). С другой стороны, в любом дифференцируемом скалярном поле ) имеем Эта примеры показывают, что с оператором «набла» нужно обращаться с большой осторожностью и при отсутствии уверенности в полученном результате его следует проверить аналитическими методами. §12. Дифференциальные операции второго порядка. Оператор Лапласа Дифференциальные операции второго порядка получаются в результате двукратного применения оператора V. 1.
- Скалярное поле
- Цилиндрические координаты
- Оператор Лапласа
- Теории поля с примерами решения и образцами выполнения
- Скалярное поле
- Производная по направлению
- Векторное поле
- Поток поля
- Дивергенция поля. Формула Остроградского-Гаусса
- Циркуляция поля
- Ротор поля. Формула Стокса
- Оператор Гамильтона
- Векторные дифференциальные операции второго порядка
- Некоторые свойства основных классов векторных полей
- Соленоидальное поле
- Потенциальное поле
- Гармоническое поле
- 🎥 Видео
Скалярное поле
В этом поле оператор V порождает векторное поле В векторном поле grad и можно определить две операции: что приводит к скалярному полю, и что приводит к векторному полю. 2. Пусть задано векторное поле . Тогда оператор V порождает в нем скалярное поле В скалярном поле div а оператор V порождает векторное поле 3.
В векторном поле оператор V порождает также векторное поле Применяя к этому полю снова оператор V, получим: а) скалярное поле Выберем в пространстве прямоугольнуюдекартову систему координат Oxyz и рассмотрим каждую из формул (1)-(5) более подробно. 1. Предполагая, что функция имеет непрерывные вторые частные производные , получим Символ называется оператором Лапласа, или лапласианом. Его можно представить как скалярное произведение оператора Гамильтона V на самого себя,т. е. Оператор Д (дельта) играет важную роль в математической физике.
Уравнение называется уравнением Лапласа. С его помощью описывается, например, стационарное распределение тепла. Скалярное поле и, удовлетворяющее условию , называется лапла-совым или гармоническим полем. Например, скалярное поле является гармоническим во воем трехмерном пространстве: из того, что получаем Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 2.
Пусть функция и имеет непрерывные частные производные второго порядка включительно. Тогда В самом деле, действуя формально, получим ибо как векторное произведение двух одинаковых «векторов». Tor же результат можно получить, используя выражения градиента и ротора в декартовых координатах Пусть задано векторное поле координаты которого P, Q, R имеют непрерывные частные производные второго порядка. Тогда получим 4. При тех же условиях, что и в пункте 3, имеем Это соотношение уже было доказано ранее путем непосредственных вычислений.
Здесь мы приведем его формальное доказательство, используя известную формулу из векторной алгебры Имеем как векторное произведение двух одинаковых «векторов». 5. Покажем, наконец, что при тех же условиях, что и ранее, Так как то, полагая в формуле для двойного векторного произведения получим Поэтому окончательно будем иметь где grad diva выражается по формуле (8), а Да для вектора надо понимать так:. В заключение приведем таблицу дифференциальных операций второго порядка. Скалярное поле Векторное поле Заштрихованные прямоугольники означают, что соответствующая операция не имеет смысла (например, градиент от. § 13.
Понятие о криволинейных координатах Во многих задачах бывает удобно определять положение точки пространства не декартовыми координатами ), а тремя другими числами (qh 42,4з), более естественно связанными с рассматриваемой части ой задачей. Если задано правило, согласно которому каждой точке М пространства отвечает определенная тройка чисел и, обратно, каждой такой тройке чисел отвечает единственная точка М, то говорят, что в пространстве задана криволинейная координатная система.
В этом случае величины ф, называют криволинейными координатами точки М. Координатными поверхностями в системе криволинейных координат qtqi, Яз называются поверхности На координатных поверхностях одна из координат сохраняет постоянное значение. Линии пересечения двух координатных поверхностей называются координатными линиями. В качестве примеров криволинейных координат рассмотрим цилиндрические и сферические координаты. 13.1.
Цилиндрические координаты
В цилиндрических координатах положение точки М в пространстве определяется тремя координатами: (р = const — полуплоскости, примыкающие к оси Oz z = const — плоскости, перпендикулярные оси Oz (рис. 41). Координатные линии: 1) линии (р) — лучи, перпендикулярные оси Oz и имеющие начало на этой оси, т.е. линии пересечения координатных поверхностей у? = const, z = const; 2) линии (ip) — окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных оси Oz 3) линии (z) — прямые, параллельные оси Связь декартовых координат точки с цилиндрическими координатами ( задается формулами 13.2.
Сферические координаты В сферических координатах положение точки Af в пространстве определяется следующими координатами: Координатные поверхности (рис.42): г = const — сферы с центром в точке О; • в = const — круговые полуконусы с осью полуплоскости, примыкающие к оси Oz. Координатные линии: 1) линии (г) — лучи, выходящие източки О; 2) линии (в) — меридианы на сфере; 3) линии — параллели на сфере. Связь декартовых координат (х, у, z) точки М с ее сферическими координатами задается формулами.
Введем единичные векторы (орты), направленные по касательным к коор-динатнымлиниям вточке М всторонувозрастанияпеременных qx, q2, соответствен но. Определение. Система криволинейных координат называется ортогональной, если в каждой точке М орты попарно ортогональны. В такой системе ортогональны и координатные линии, и координатные поверхности. Примерами ортогональных криволинейных координат служатсистемы цилиндрических и сферических координат.
Мы ограничимся рассмотрением только ортогональных систем координат. Пусть — радиус-вектор точки М — Тогда можно показать, что Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты Аналогично для сферических координат имеем Величины являются дифференциалами длин дуг соответс твующих координатных линий.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Скалярные и векторные величины, основные определения.Скачать
Оператор Лапласа
Оператор Лапласа — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом . Функции F он ставит в соответствие функцию
Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции.
Градиент— вектор, показывающий направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля). Например, если взять в качестве высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма». Величина (модуль) вектора градиента равна скорости роста в этом направлении. Для случая трёхмерного пространства, градиентом называется векторная функция с компонентами , где — некоторая скалярная функция координат x,y,z.
Если — функция n переменных то ее градиентом называется n-мерный вектор
Компоненты которого равны частным производным по всем ее аргументам. Градиент обозначается grad, или с использованием оператора набла,
Из определения градиента следует, что:
Смысл градиента любой скалярной функции f в том, что его скалярное произведение с бесконечно малым вектором перемещения дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена f, то есть линейную (в случае общего положения она же главная) часть изменения f при смещении на . Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат x i, то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку dx — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе.
Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:
Или опуская по правилу Эйнштейна знак суммы,
Дивергенция — дифференциальный оператор, отображающий векторное поле на скалярное (то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле» (точнее — насколько расходятся входящий и исходящий поток).
Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учетом знака. Поэтому можно дать более короткое определение дивергенции:
дивергенция — это дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.
Оператор дивергенции, применённый к полю F, обозначают как или
Определение дивергенции выглядит так:
где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю. Это определение, в отличие от приводимого ниже, не привязано к определённым координатам, например, к декартовым, что может представлять дополнительное удобство в определённых случаях. (Например, если выбирать окрестность в форме куба или параллелепипеда, легко получаются формулы для декартовых координат, приведённые в следующем параграфе).
таким образом значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля gradF в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом то есть в виде скалярного произведения оператора набла на себя.
Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Теории поля с примерами решения и образцами выполнения
Теория поля — крупный раздел физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.
К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы — все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т. д.
Математическим ядром теории поля являются такие понятия, как градиент, поток, потенциал, дивергенция, ротор, циркуляция и другие. Эти понятия важны и в усвоении основных идей математического анализа функций многих переменных.
Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке М этой области соответствует определенное число U = U(M), говорят, что в области определено (задано) скалярное поле (или функция точки). Иначе говоря, скалярное поле — это скалярная функция U(М) вместе с ее областью определения. Если же каждой точке М области пространства соответствует некоторый вектор 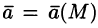
Примерами скалярных полей могут быть поля температуры (воздуха, тела, …), атмосферного давления, плотности (массы, воздуха, …), электрического потенциала и т.д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидкости (ветра), магнитное поле, поле плотности электрического тока и т. д.
Если функция 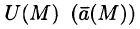
Далее будем рассматривать только стационарные поля.
Если V — область трехмерного пространства, то скалярное поле U можно рассматривать как функцию трех переменных х, у, z (координат точки М):
(Наряду с обозначениями 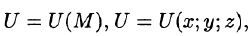
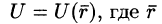
Если скалярная функция U (М) зависит только от двух переменных, например х и у, то соответствующее скалярное поле U(х; у) называют плоским.
Аналогично: вектор 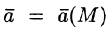
Вектор 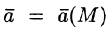
где P(x;y;z), Q(x;y;z ), R(x;y;z) — проекции вектора 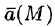
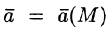
Векторное поле называется однородным, если 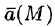
В дальнейшем будем предполагать, что скалярные функции (U(x;y;z) — определяющая скалярное поле, P(x;y;z), Q(x;y;z) и R(x; у; z) — задающие векторное поле) непрерывны вместе со своими частными производными.
Пример:
Функция 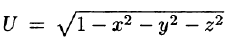
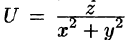
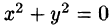
Пример:
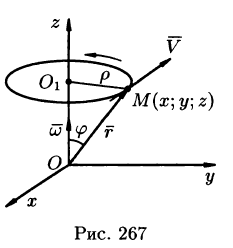
Найти поле линейной скорости 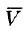
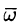
Решение:
Угловую скорость представим в виде вектора 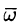
Построим радиус-вектор 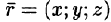
Численное значение линейной скорости 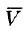
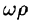
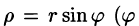
Вектор скорости 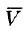
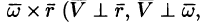
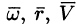
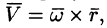
или
Поле линейных скоростей 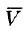
Видео:Оператор Набла. Градиент. Дивергенция. Ротор. Лапласиан.Скачать

Скалярное поле
Поверхности и линии уровня:
Рассмотрим скалярное поле, задаваемое функцией U = U(x,y,z). Для наглядного представления скалярного поля используют поверхности и линии уровня.
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(М) принимает постоянное значение, т. е.
Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).
Для скалярного поля, образованного функцией
поверхностями уровня является множество концентрических сфер с центрами в начале координат: 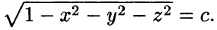
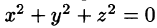
Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой круговые цилиндры, общей осью которых служит нить.
В случае плоского поля U — U(х; у) равенство U(x; у) = с представляет собой уравнение линии уровня поля, т. е. линия уровня —это линия на плоскости Оху, в точках которой функция U (х; у) сохраняет постоянное значение.
В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.
Линии уровня применяются в математике при исследовании поверхностей методом сечений (см. п. 12.9).
Производная по направлению
Для характеристики скорости изменения поля U =U(М) в заданном направлении введем понятие «производной по направлению».
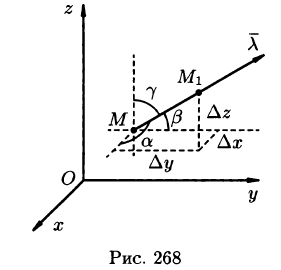
Возьмем в пространстве, где задано поле U = U(x;y;z), некоторую точку М и найдем скорость изменения функции U при движении точки М в произвольном направлении 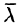
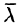
Приращение функции U, возникающее при переходе от точки М к некоторой точке 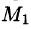
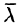
Производной от функции U = U(M) в точке М по направлению 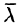
Производная по направлению 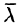
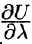
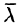
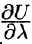
где 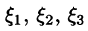
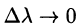
Переходя к пределу при 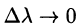
В случае плоского поля U = U(x;y) имеем:
Формула (70.2) принимает вид:
Замечание:
Понятие производной по направлению является обобщением понятия частных производных 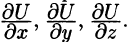
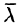
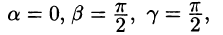
Пример:
Найти производную функции 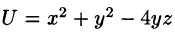
Решение:
Находим вектор 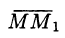
Находим частные производные функции и вычисляем их значения в точке М:
Следовательно, по формуле (70.2) имеем:
Поскольку jj^- Градиент скалярного поля и его свойства
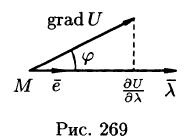
В каком направлении 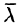
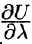
Можно заметить, что правая часть равенства (70.2) представляет собой скалярное произведение единичного вектора
и некоторого вектора
Вектор, координатами которого являются значения частных производных функции U(x,y,z) в точке M(x;y,z), называют градиентом функции и обозначают gradU, т. е.
Отметим, что grad U есть векторная величина. Говорят: скалярное поле U порождает векторное поле градиента U. Теперь равенство (70.2) можно записать в виде
где 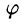
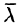
Из формулы (70.3) сразу следует, что производная по направлению достигает наибольшего значения, когда 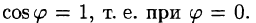
В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других дисциплинах.
Приведем важные свойства градиента функции.
1.Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
Действительно, по любому направлению вдоль поверхности уровня 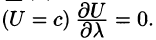
Доказываются эти свойства на основании определения градиента. Докажем, например, последнее свойство. Имеем:
Замечание. Приведенные свойства градиента функции остаются справедливыми и для плоского поля.
Пример:
Найти наибольшую скорость возрастания функции
Решение:
Наибольшая скорость возрастания функции равна
Отметим, что функция U будет убывать с наибольшей скоростью 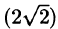
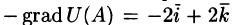
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Векторное поле
Векторные линии поля:
Рассмотрим векторное поле, задаваемое вектором 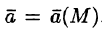
Векторной линией поля 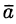
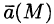
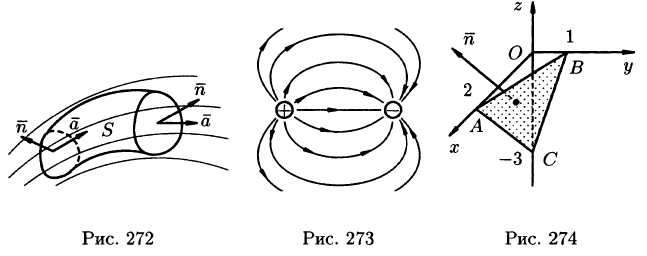
Это понятие для конкретных полей имеет ясный физический смысл. Например, в поле скоростей текущей жидкости векторными линиями будут линии, по которым движутся частицы жидкости (линии тока); для магнитного поля векторными (силовыми) линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Изучение векторного поля обычно начинают с изучения расположения его векторных линий. Векторные линии поля
описываются системой дифференциальных уравнений вида
Действительно, пусть PQ — векторная линия поля, 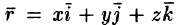
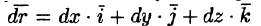
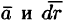
Пример:
Найти векторные линии поля линейных скоростей тела, вращающегося с постоянной угловой скоростью 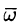
Решение:
Это поле определено вектором 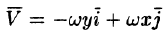
Интегрируя, получим: 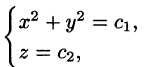
Поток поля
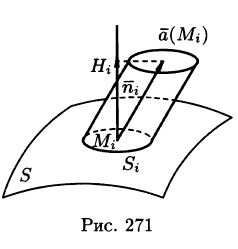
Пусть векторное поле образовано вектором (71.1). Для наглядности будем считать 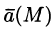
Выберем определенную сторону поверхности S. Пусть 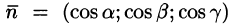
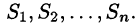
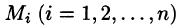
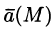
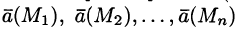
Будем приближенно считать каждую площадку плоской, а вектор 
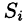
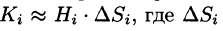
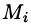
Точное значение искомого количества жидкости получим, взяв предел найденной суммы при неограниченном увеличении числа элементарных площадок и стремлении к нулю их размеров (диаметров 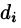
Независимо от физического смысла поля 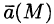
Потоком вектора 
Рассмотрим различные формы записи потока вектора. Так как
где 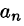
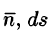
Иногда формулу (71.3) записывают в виде
где вектор 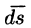
— проекции вектора 

Используя взаимосвязь поверхностных интегралов I и II рода (см. формулу (58.8)), поток вектора можно записать как
Отметим, что поток К вектора а есть скалярная величина. Величина К равна объему жидкости, которая протекает через поверхность S за единицу времени. В этом состоит физический смысл потока (независимо от физического смысла поля).
Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объем V. Тогда поток вектора записывается в виде
В этом случае за направление вектора п обычно берут направление внешней нормали и говорят о потоке изнутри поверхности S (см. рис. 272).
Если векторное поле 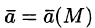

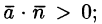
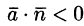
При этом если К > 0, то из области V вытекает больше жидкости, чем в нее втекает. Это означает, что внутри области имеются дополнительные источники.
Если К
Пример:
Найти поток вектора 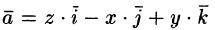
Решение:
Поток найдем методом проектирования на три координатные плоскости. Для этого воспользуемся формулой (71.5). В нашем случае Р = z, Q = —х, R = у. Имеем:
Расчленим этот поверхностный интеграл на три слагаемых, затем сведем их вычисление к вычислению двойных интегралов. Нормаль к верхней стороне треугольника образует с осью Ох тупой угол, с осью Оу — тупой, а с осью Oz — острый угол. (Единичный вектор данной плоскости есть 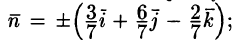
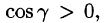
Итак, 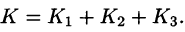
В результате имеем:
Пример:
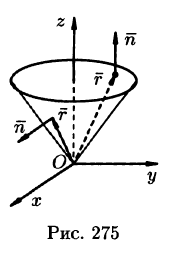
Найти поток радиус-вектора 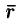
Решение:
Очевидно, что
т. к.
Дивергенция поля. Формула Остроградского-Гаусса
Важной характеристикой векторного поля (71.1) является так называемая дивергенция, характеризующая распределение и интенсивность источников и стоков поля.
Дивергенцией (или расходимостью) векторного поля
в точке М называется скаляр вида 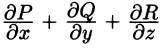
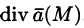
Отметим некоторые свойства дивергенции.
- Если
— постоянный вектор, то
где с = const.
т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
- Если U — скалярная функция,
— вектор, то
Эти свойства легко проверить, используя формулу (71.6). Докажем, например, справедливость свойства 4.
Так как 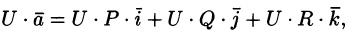
Используя понятия потока и дивергенции векторного поля, запишем известную в анализе (см. (58.9)) формулу Остроградского-Гаусса
в так называемой векторной форме.
Рассматривал область V, ограниченную замкнутой поверхностью S, в векторном поле (71.1), можно утверждать, что левая часть формулы (71.7) есть поток вектора 

(в котором она чаще всего и встречается).
Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность S (в направлении внешней нормали, т. е. изнутри) равен тройному интегралу от дивергенции этого поля по объему V, ограниченному данной поверхностью.
Используя формулу (71.8), можно дать другое определение дивергенции векторного поля 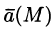
По теореме о среднем для тройного интеграла (см. п. 54.1) имеем:
где 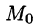
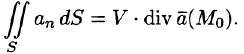
Пусть поверхность S стягивается в точку. Тогда 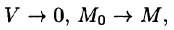
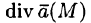
Дивергенцией векторного поля в точке М называется предел отношения потока поля через (замкнутую) поверхность S, окружающую точку М, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку
Определение (71.9) дивергенции эквивалентно (можно показать) определению (71.6).
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
Исходя из физического смысла потока (обычно условно считают, что 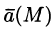
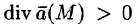
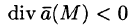
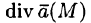
Понятно, что если в объеме V, ограниченном замкнутой поверхностью S, нет ни источников, ни стоков, то
Векторное поле, в каждой точке которого дивергенция поля равна нулю, т. е. 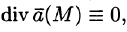
Пример:
Найти дивергенцию поля линейных скоростей 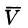
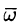
Решение:
Примем ось вращения жидкости за ось Oz. Тогда, как показано ранее (см. пример 69.2), 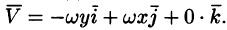
Поле 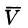
Циркуляция поля
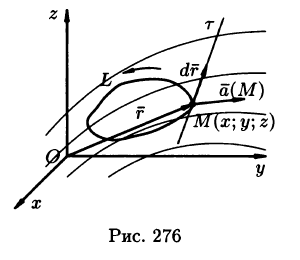
Пусть векторное поле образовано вектором (71.1). Возьмем в этом поле некоторую замкнутую кривую L и выберем на ней определенное направление.
Пусть 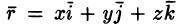
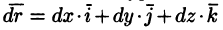
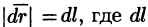
Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора 
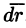

Рассмотрим различные формы записи циркуляции. Так как
где 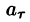

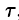
Циркуляция С, записанная в виде (71.12) имеет простой физический смысл: если кривая L расположена в силовом поле, то циркуляция — это работа силы 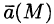
Отметим, что вдоль замкнутых векторных линий циркуляция отлична от нуля, потому что в каждой точке векторной линии скалярное произведение 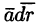

Пример:
Найти циркуляцию вектора поля линейных скоростей вращающегося тела (см. пример 69.2) 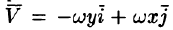
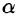
Решение:
Будем считать, что направление нормали к плоскости 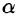
где S — площадь поверхности, ограниченной кривой L (см. 56.17).
Заметим, что если нормаль к поверхности S образует угол 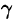
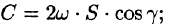
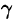
Пример:
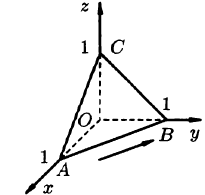
Вычислить циркуляцию векторного поля
вдоль периметра треугольника с вершинами A(1;0;0), В(0;1;0), С(0;0;1) (см. рис. 277).
Решение:
Согласно формуле (71.12), имеем:
На отрезке AB: x + у = 1, z = 0, следовательно,
На отрезке ВС: у + z = 1, х = 0, следовательно,
На отрезке СА: х + z = 1, у = 0, следовательно,
Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
называется вектор, обозначаемый 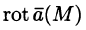
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
Отметим некоторые свойства ротора.
- Если
— постоянный вектор, то
т. е. ротор суммы двух векторов равен сумме роторов слагаемых.
- Если U — скалярная функция, а
— векторная, то
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
Левая часть формулы (71.14) представляет собой циркуляцию вектора 
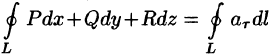
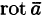
Следовательно, формулу Стокса можно записать в виде
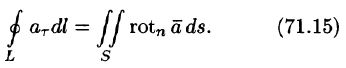
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре L и выбор стороны у поверхности S согласованы между собой так же, как в теореме Стокса.
Формула (71.15) показывает, что циркуляция вектора 

Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
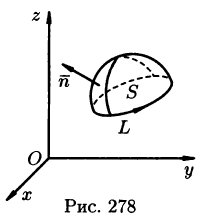
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки S с контуром L, содержащей точку М.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
где 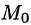
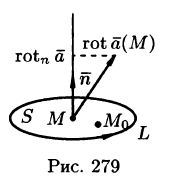
Тогда формулу (71.15) можно записать в виде
Пусть контур L стягивается в точку М. Тогда 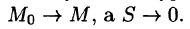
Ротором вектора 
Как видно из определения, ротор вектора 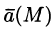
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор поля линейных скоростей твердого тела, вращающегося вокруг оси Oz с постоянной угловой скоростью (пример 69.2) 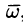
По определению ротора
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 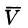
Замечание:
Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке S.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
Оператор Гамильтона
Векторные дифференциальные операции первого порядка:
Основными дифференциальными операциями (действиями) над скалярным полем U и векторным полем 
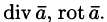
Эти операции удобно записывать с помощью так называемого оператора Гамильтона
Этот символический вектор называют также оператором 


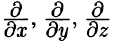
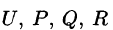
Применяя оператор Гамильтона, получим дифференциальные операции первого порядка:
Оператор Гамильтона применяется для записи и других операций и для вывода различных формул в теории поля. При действиях с ним надо пользоваться правилами векторной алгебры и правилами дифференцирования.
В частности, производная по направлению (70.2) может быть записана в виде
где
Векторные дифференциальные операции второго порядка
После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применить этот оператор. В результате получаются дифференциальные операции второго порядка. Нетрудно убедиться, что имеется лишь пять дифференциальных операций второго порядка:
(Понятно, что операция 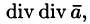
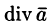
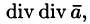
Запишем явные выражения для дифференциальных операций второго порядка, используя оператор Гамильтона. Заметим при этом, что оператор действует только на множитель, расположенный непосредственно за оператором.
Правая часть этого равенства называется оператором Лапласа скалярной функции U и обозначается 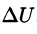
Дифференциальное уравнение Лапласа 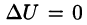
Замечание. К равенству (72.1) можно прийти, введя в рассмотрение скалярный оператор дельта:
(который тоже называют оператором Лапласа).
2. 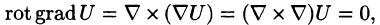
4. 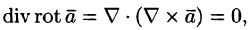
так как двойное векторное произведение обладает свойством
Здесь 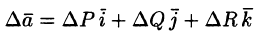

Некоторые свойства основных классов векторных полей
Соленоидальное поле
Напомним, что векторное поле 
Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела (см. пример 71.4); магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и другие.
Приведем некоторые свойства соленоидального поля.
- В соленоидальном поле
поток вектора через любую замкнутую поверхность равен нулю. Это свойство непосредственно вытекает из формулы (71.8). Таким образом, соленоидальное поле не имеет источников и стоков.
- Соленоидальное поле является полем ротора некоторого векторного поля, т. е. если
, то существует такое поле
, что
. Вектор
называется векторным потенциалом поля
.
Любое из свойств 1-2 можно было бы взять в качестве определения соленоидального поля.
Доказывать свойство 2 не будем. Отметим лишь, что обратное утверждение — поле ротора векторного поля есть соленоидальное — нами доказано (выше мы показали, что 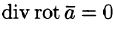
3. В соленоидальном поле 
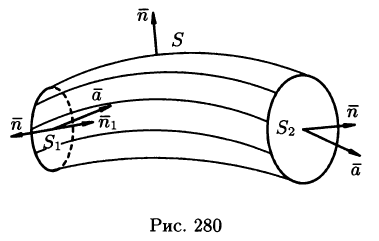
Рассмотрим векторную трубку между двумя ее произвольными сечениями 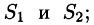
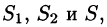
где n — внешняя нормаль.
Так как на боковой поверхности векторной трубки нормаль п перпендикулярна к векторам поля, то 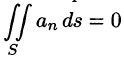
Переменив направление нормали на площадке 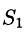
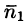
В поле скоростей текущей жидкости полученный результат означает, что количество жидкости, втекающей в трубку за единицу времени, равно количеству жидкости, вытекающей из нее.
Потенциальное поле
Векторное поле 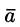
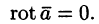
Приведем основные свойства потенциального поля.
Свойство 1. Циркуляция потенциального поля 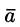
Это непосредственно вытекает из формулы (71.14). Следовательно,
В частности, для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости равенство С = 0 означает, что в потоке нет замкнутых струек, т. е. нет водоворотов.
Свойство 2. В потенциальном поле 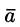
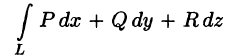
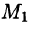
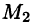
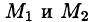
Это свойство вытекает из свойства 1. Действительно, взяв в поле две точки 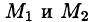
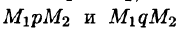
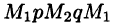
Учитывая свойства криволинейного интеграла, получаем:
Свойство 3. Потенциальное поле является полем градиента некоторой скалярной функции U(x; y; z), т. е. если 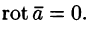
Из равенства 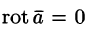
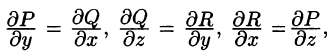
Отсюда: 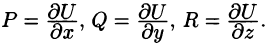
т. е. вектор поля 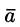
Замечание. Из равенства rot grad U = 0 следует обратное утверждение — поле градиента скалярной функции U = U(x;y; z) является потенциальным.
Из равенства 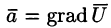
где 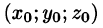
Произвольное же векторное поле требует задания трех скалярных функций (P(x;y;z), Q(x;y;z), R(x;y,z) — проекции вектора поля на оси координат).
Замечание. Определение потенциального поля может быть дано иначе — векторное поле 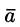
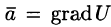
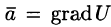
Пример:
Установить потенциальность поля
и найти его потенциал.
Решение:
Следовательно, поле вектора 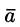
Найдем потенциал U по формуле (73.1), выбирая в качестве фиксированной точки начало координат, т. е. 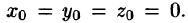
Гармоническое поле
Векторное поле 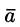
Примером гармонического поля является поле линейных скоростей стационарного безвихревого потока жидкости при отсутствии в нем источников и стоков.
Так как поле 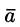
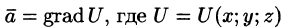
Но так как поле одновременно и соленоидальное, то
или, что то же самое,
т. е. потенциальная функция U гармонического поля а является решением дифференциального уравнения Лапласа. Такая функция называется, как уже упоминали, гармонической.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎥 Видео
Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

Введение в векторы и скаляры (видео 1)| Векторы. Прямолинейное движение | ФизикаСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Оператор Набла за 10 минут. Градиент, Дивергенция, Ротор, ЛапласианСкачать

Лекция 18. Скалярное произведение векторов и его свойства.Скачать

Скалярное и векторное поля. Определения и отличия.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Оператор ЛапласаСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Математика без Ху!ни. Свойства скалярного и векторного произведений.Скачать

✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Скалярное произведение векторов.Скачать

Дивергенция векторного поляСкачать


















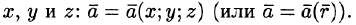
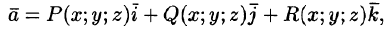
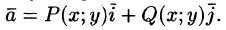
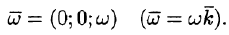
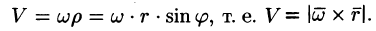
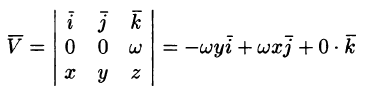
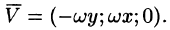


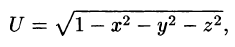
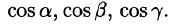
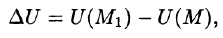
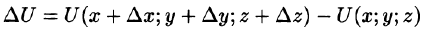
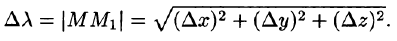
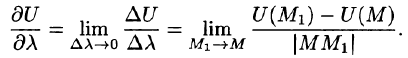
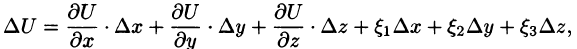
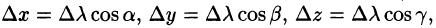
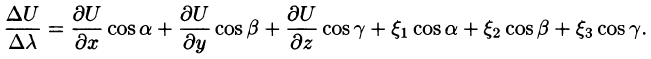
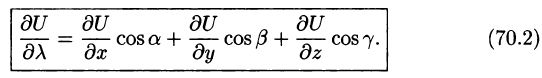
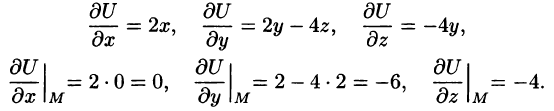
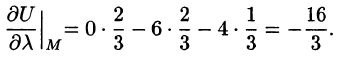
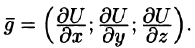
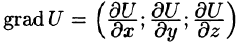
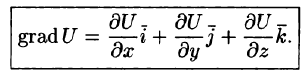
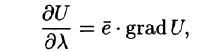
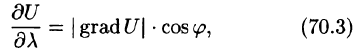
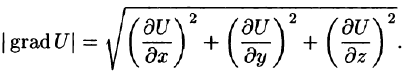
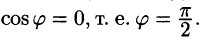
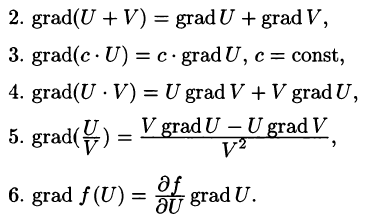
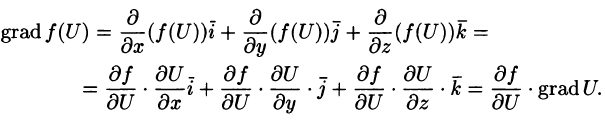
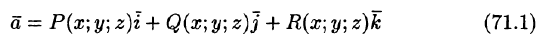
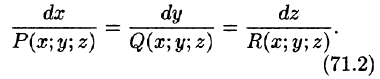
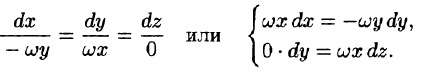
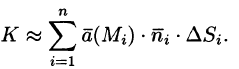
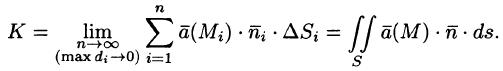

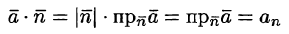

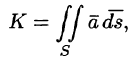
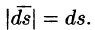
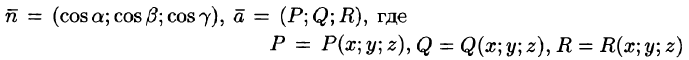
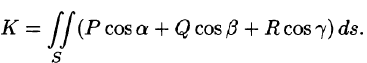
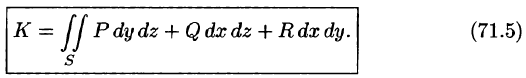
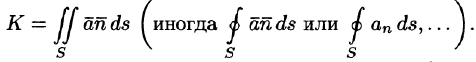
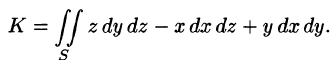
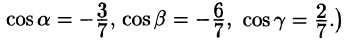
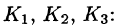
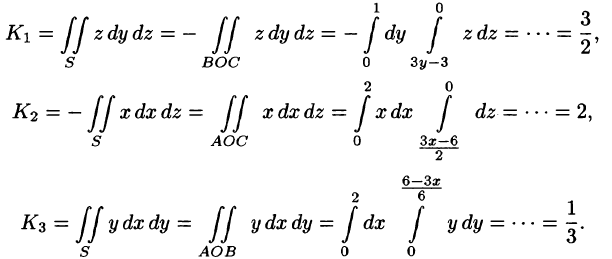
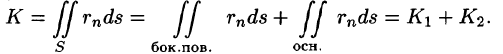
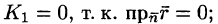
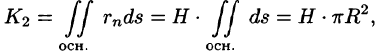
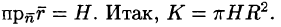
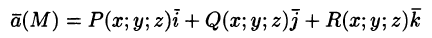
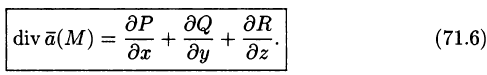
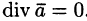
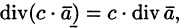 где с = const.
где с = const.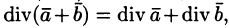 т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.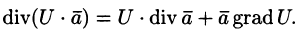
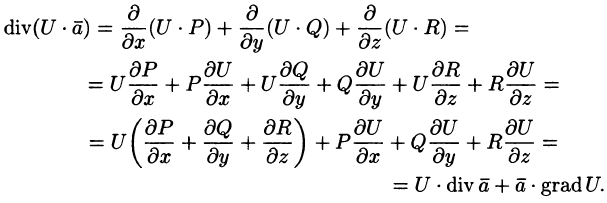
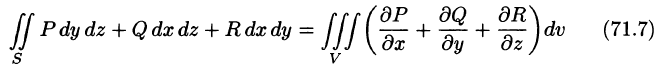
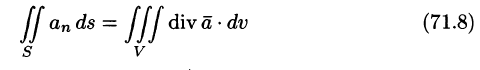
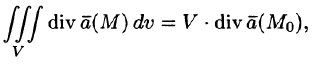
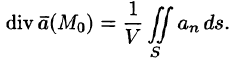
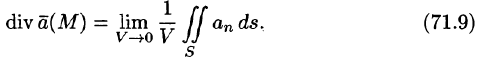
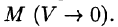
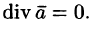
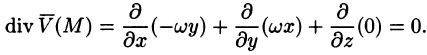
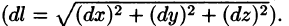
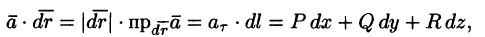

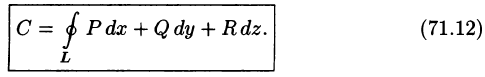
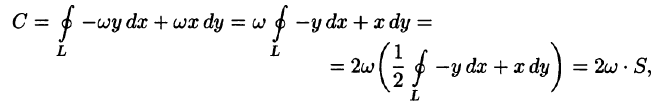
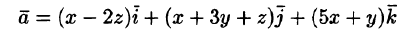
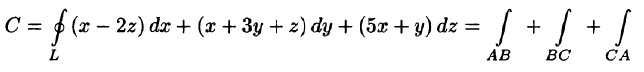
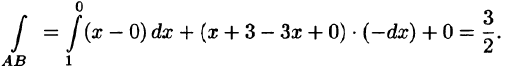
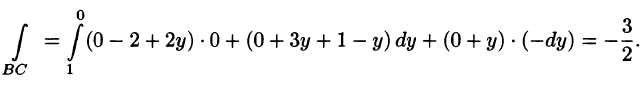
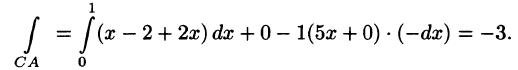
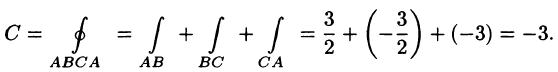
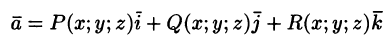
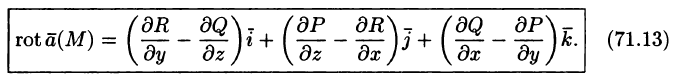
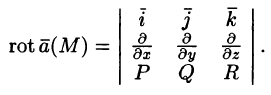
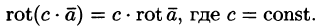
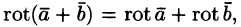 т. е. ротор суммы двух векторов равен сумме роторов слагаемых.
т. е. ротор суммы двух векторов равен сумме роторов слагаемых.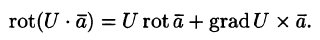
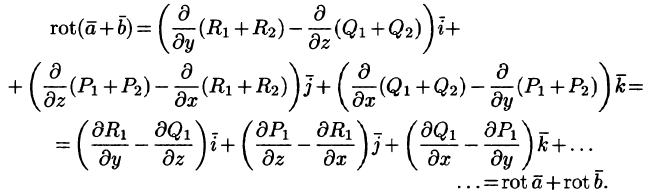
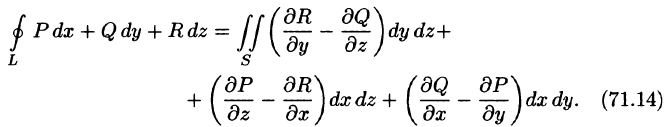
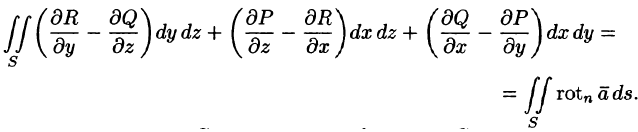
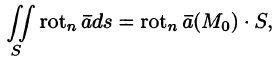
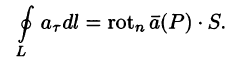
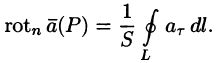
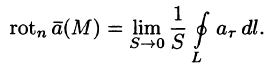
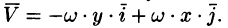
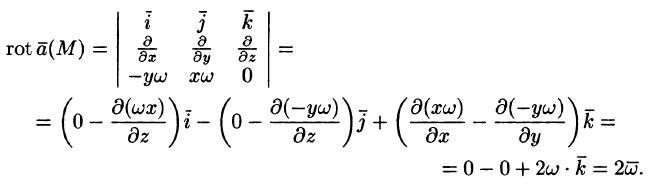
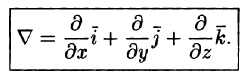
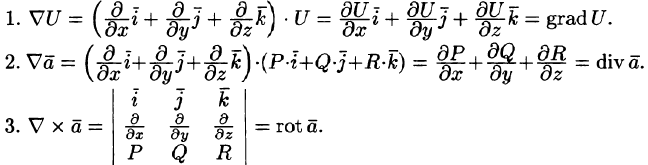
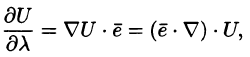
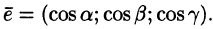
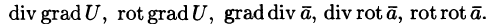
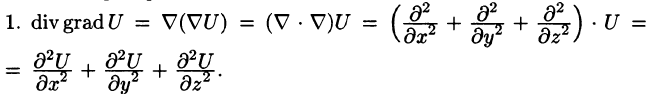
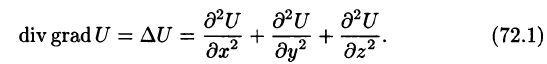
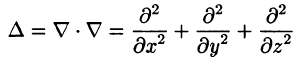
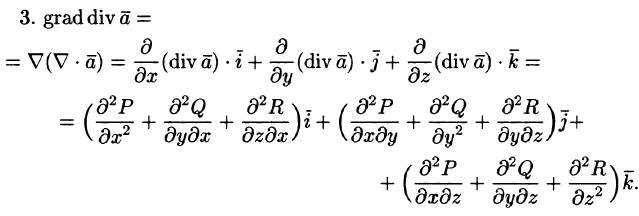
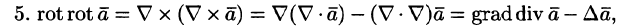
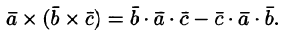
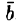 , что
, что 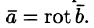 . Вектор
. Вектор