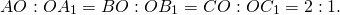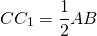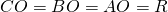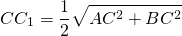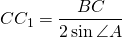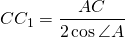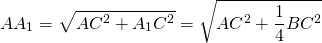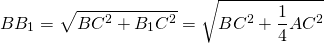Медиана равна радиусу описанной окружности (6 видео)

Свойства медианы в прямоугольном треугольнике с доказательствами

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.

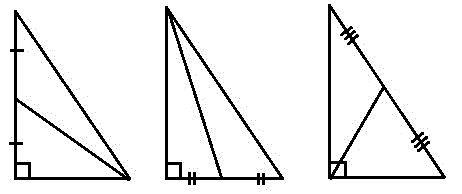
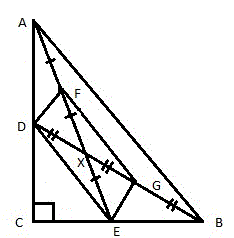
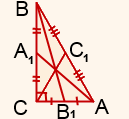
Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Содержание

Свойства медианы в прямоугольном треугольнике
Доказательства свойств
Первое свойство
Доказательство:
Второе свойство
Доказательство:
Третье свойство
Доказательство:
Все формулы медианы прямоугольного треугольника
Медиана в прямоугольном треугольнике
12 Comments
🎦 Видео

Видео:Строим треугольник по стороне, медиане и радиусу описанной окружности (Задача 8).Скачать

Свойства медианы в прямоугольном треугольнике

Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Видео:Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

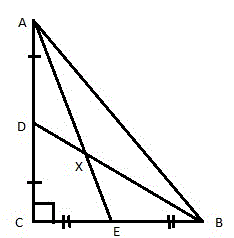
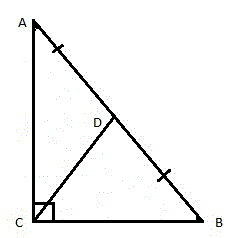
Рассмотрим прямоугольный треугольник ABC. Проведем две медианы AE и BD, которые пересекаются в точке X (рис. 2).

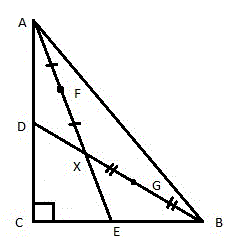
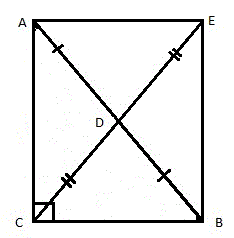
Середины отрезков AX и BX обозначим, соответственно, буквами F и G (рисунок 3).

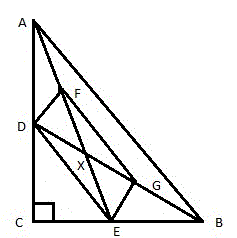
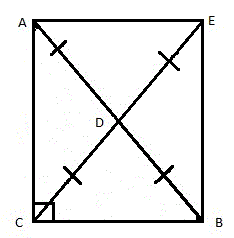
Соединим между собой точки (D, F, G и E) и получим четырёхугольник DFGE (рис. 4).

Сторона DE этого четырёхугольника будет средней линией треугольника ABC. Согласно определению: отрезок, соединяющий середины двух сторон треугольника, является его средней линией. При этом по свойству средняя линия параллельна не пересекающейся с ней стороне и равна половине этой стороны, то есть.
DE || AB и DE = AB / 2.

Аналогично сторона FG треугольника AXB будет его средней линией.
FG || AB и FG = AB / 2

Отсюда следует, что отрезки DE и FG являются параллельными и равными. Следовательно, четырехугольник DFGE – параллелограмм (по признаку параллелограмма).

Так как диагонали параллелограмма в точке пересечения делятся пополам, то
FX=XE, GX=XD

Так как AF = FX (по построению), то и AF = FX = XE, аналогично DX = XG = GB.

Получается, что точка X делит обе медианы AE и BD в соотношении 2 к 1 считая от вершины треугольника.

Аналогично, мы сможем доказать, что точка пересечения 3-ей медианы, проведенной из прямого угла к гипотенузе, с медианой AE (или BD) будет делить ее в соотношении 2 к 1, считая от вершины. То есть наша 3-я медиана также пройдет через точку X. Отсюда следует, что все 3 наши медианы пересекаются в одной точке.

Что и требовалось доказать.

Второе свойство

Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

Чтобы доказать это свойство рассмотрим прямоугольный треугольник ABC и проведём медиану к гипотенузе. Точку ее пересечения с гипотенузой обозначим буквой D (рис. 6).

Отразим симметрично наш треугольник ABC относительно отрезка AB (рисунок 7). В результате получим четырёхугольник AEBC, в котором AD=DB (поскольку CD медиана к стороне AB) и CD=DE (по построению). То есть диагонали четырехугольника AEBC пересекаются и точкой пересечения делятся пополам. Отсюда следует, что AEBC является параллелограммом (по признаку параллелограмма).

Один из признаков прямоугольника говорит о том, что параллелограмм является прямоугольником, если хотя бы один из его углов прямой. Поскольку ∠ACB прямой (по построению), то AEBC — прямоугольник.

Поскольку диагонали прямоугольника равны и в точке пересечения делятся пополам (свойство прямоугольника), то AB = CE и AD = DB = CD = DE.

Так как AB = AD + DB, AD = BD и СD = AD = BD, то получается, что медиана AD, проведенная к гипотенузе AB равна половине ее длины.

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

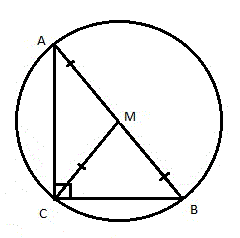
Опишем вокруг прямоугольного треугольника ABC окружность.

Поскольку точка C уже лежит на окружности, то для того, чтобы доказать, что медиана CM является радиусом, нам надо доказать, что точка M – центр описанной окружности (т.е. равноудалена от нее).

Так как медиана делит отрезок пополам, а медиана проведенная к гипотенузе равна ее половине (согласно доказанному выше свойству), то точка M будет равноудалена от всех вершин треугольника, которые в свою очередь касаются окружности (рисунок 8).

Отсюда следует, что окружность, описанная вокруг прямоугольного треугольника ABC будет иметь центр на середине гипотенузы (в точке M), а медиана CM будет радиусом описанной окружности.

Что и требовалось доказать.

Понравилась статья, расскажите о ней друзьям:

Видео:РадиусВписаннойОкружностиСкачать

Все формулы медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.

Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

Медиана равна радиусу и половине гипотенузы, ( M ):

Формула длины через катеты, ( M ):

Формула длины через катет и острый угол, ( M ):

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Медиана в прямоугольном треугольнике

Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.

Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:

Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.

Например:

Видео:Задача 6 №27892 ЕГЭ по математике. Урок 126Скачать

12 Comments

Информация очень хорошая. Правда не помогла мне решить задачу, которую мой сын не решил на контрольной. приведу условие:
Из прямого угла треугольника проведена медиана на гипотенузу. Длина медианы 6см. Определить катеты.

Петр, данных для определения катетов недостаточно. Длина гипотенузы в 2 раза больше длины медианы — 12 см. Это всё, что можно сказать по данным условия.

не правда надо провести высоту из прямого угла дальше все получится. один катет равен 6 а второй 2 корня из 22

Сумма квадратов катетов равна квадрату гипотенузы. Проверим 6^2+(2*корень из 22)^2
=36+4*22=36+88=124. Квадрат гипотенузы 12^2=144

попробуйте составить уравнение,обозначив 1 из катетов через х а 2-ой катет обозначьте буквами…x^2+BC^2=12^2…да числа не очень,но это 1 способ..решаю дальше:BC^2=12^2-x^2
BC^2=11x
X^2+11X=144
X^2=12
x(1 катет)=корню из 12,а «-ой катет=11 корней из 12….решал на основе теоремы пифагора

задача имеет бесконечное кол-во решений. решение возможно только в виде формулы или графика, где описана зависимость между катетами и гипотенузой

Да просто треугольник медианой делится на два треугольника с одинаковыми катетами, а дальше как уже предлагалось выше Пифагор во спасение))

А кто вам сказал, что медиана в прямоугольном треугольнике является еще и высотой? Откуда у вас два треугольника с одинаковыми катетами?

Спасибо за понятное объяснение, но у нас задача немного другая.
В прямоугольном треугольнике АВС угол С= 90 градусов,медиана ВВ1 равна 10 см.Найдите медианы АА1 СС1, если известно, что АС=12 см.( используя т.Пифагора.

1) Рассмотрим треугольник BB1C. В нём угол С равен 90 градусов, BB1=10 см, B1C=6 см (так как BB1 — медиана). По теореме Пифагора находим BC: BC=8 см. 2) Рассмотрим треугольник AA1C. В нём угол С равен 90 градусов, AC=12 см, AA1=4 см (так как BB1 — медиана). По теореме Пифагора находим AA1: AA1=4√10 см.3) Из треугольника ABC по теореме Пифагора найдём AB: AB=4√13 см. 4) CC1=1/2 AB (как медиана, проведённая к гипотенузе), CC1=2√13 см.
Где-то так.