Поворот окружности на 60 градусов (2 видео)

Угол поворота, угол произвольной величины

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Содержание

Поворот точки вокруг точки
Полный оборот
Угол поворота
Направление поворота
Величина угла поворота, угол произвольной величины
Поворот фигуры вокруг точки на угол
Поворот. Задачи
Урок геометрии по теме «Поворот»
Презентация к уроку
🌟 Видео

Видео:9 класс, 33 урок, ПоворотСкачать

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .

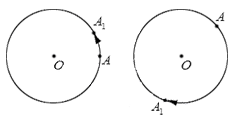
Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:

Видео:Поворот ромба на 60 градусов относительно вершины.Скачать

Полный оборот

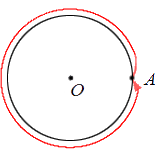
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .

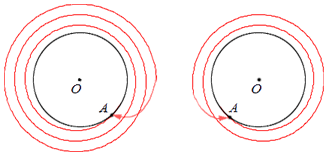
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .

Разберем характеристики угла поворота подробнее.

Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать

Направление поворота

Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

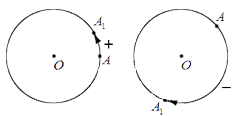
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Видео:Построить угол 60°Скачать

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.

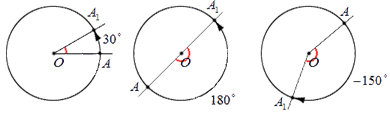
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :

Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

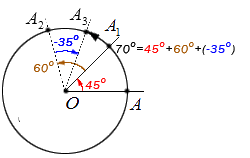
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:

Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .

По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .

Видео:ПоворотСкачать

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

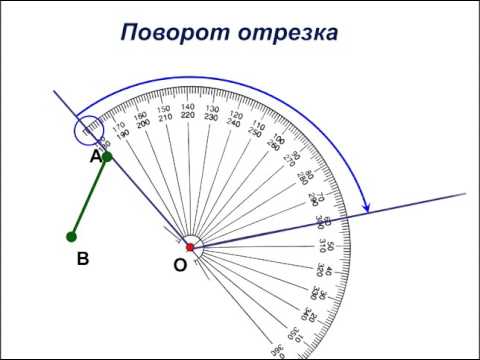
Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .

Видео:84 Поворот на 60 градусовСкачать

Поворот. Задачи

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Это занятие будет посвящено теме «Поворот». Мы решим несколько задач на упомянутую тему, но для начала повторим понятие движения. После чего рассмотрим один из видов движения – поворот, перечислим его свойства и особенности. Решим вместе с преподавателем задачи на эту тему.

Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур»

Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Урок геометрии по теме «Поворот»

Презентация к уроку

Цели урока:

Образовательные

ввести понятие поворота и доказать, что поворот есть движение;
рассмотреть поворот отрезка, в зависимости от центра поворота (центр поворота лежит вне отрезка, на отрезке и является одним из концов отрезка);
научить построению отрезка при повороте его на данный угол;
проверить усвоение материала, изученного на предыдущих уроках и материала, пройденного на этом уроке.

Развивающие

развивать умение анализировать условие задачи, строить логическую цепочку при решении задач, обоснованно делать выводы;
развивать мыслительный процесс, познавательный интерес, математическую речь учащихся;

Воспитательные

воспитывать внимательность, наблюдательность, положительное отношение к обучению.

Содержание темы: урок по геометрии разработан для учащихся 9 класса.

Тип урока: урок изучения нового материала и промежуточного контроля усвоения учащимися пройденного на этом уроке и изученного ранее материала.

Организационные формы общения: коллективная, индивидуальная, фронтальная, в парах.

Структура занятия:

Мотивационная беседа с учащимися с последующей постановкой целей;
Проверка домашнего задания;
Актуализация опорных знаний;
Обогащение знаний;
Закрепление изученного материала;
Проверка усвоения изученного материала (тестирование с последующей взаимопроверкой);
Подведение итога занятия (рефлексия);
Домашнее задание.

Оформление: мультимедийный проектор, экран, ноутбук, компьютерная презентация, сигнальные карточки.

Мотивационная беседа.

Без движения — жизнь только летаргический сон.
Жан Жак Руссо

I. Сообщение темы, целей и хода урока. (СЛАЙД 2)

— Ребята, Вы знаете какую важную роль имеет движение в жизни человека, общества, науки. Большую роль играет движение и в математике: преобразование графиков, отображение точек, фигур, плоскостей – всё это движение. На предыдущих уроках мы с Вами рассмотрели несколько видов движения. Сегодня мы познакомимся ещё с одним видом движения: поворотом. Тема урока: поворот.

И наш урок тоже является примером движения, только движения не с физической точки зрения, а движением в умственном развитии, познании нового и приобретения новых знаний. В течение всего урока Вы будете выполнять различные задачи, тесты. Поэтому будьте активны, продвигайтесь в своих знаниях вперёд на протяжении всего урока и улучшайте свои результаты от одного этапа к другому!

В течение всего урока, как мою речь, так и вашу будет сопровождать презентация, которая поможет проверить правильность выполнения Вами домашней работы, предложенных тестов и самостоятельно решённых задач.

II. Проверка домашнего задания.

С помощью СЛАЙДОВ 3-5 проверить решение № 1165.

III. Актуализация опорных знаний.

Тест №1. (СЛАЙДЫ 6-13)

После выполнения теста ребята обмениваются тетрадями и выполняют взаимопроверку.

IV. Изучение нового материала. (обогащение знаний)

(СЛАЙД 14) Отметим на плоскости точку О (неподвижная точка), и зададим угол a – угол поворота. Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка M отображается в такую точку M₁, что OM =OM₁ и угол MOM₁ = a.

(СЛАЙД 15) При этом точка O остаётся на месте, т.е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки O в одном и том же направлении на угол a по часовой стрелки или против часовой стрелки.

(СЛАЙД 16) Точка О называется центром поворота, a – угол поворота. Обозначается Р_о a .

(СЛАЙД 17) Если поворот выполняется по часовой стрелке, то угол поворота a считается отрицательным. Если поворот выполняется против часовой стрелки, то угол поворота – положительный.

— Ребята, давайте вспомним понятие движения. Как Вы думаете, является ли поворот движением? (высказывают предположения)

— Поворот – является движением, т.е. отображением плоскости на себя. Докажем это.

(СЛАЙД 18 или СЛАЙД 19)

(Доказательство может выполнить сильный ученик по СЛАЙДУ 18. В этом случае можно сразу после доказательства перейти к СЛАЙДУ 20. Доказательство может выполнить учитель вместе с классом по СЛАЙДУ 19, на котором отображаются этапы доказательства.)

V. Закрепление изученного материала.

Задание. Построить точку M₁, которая получается из точки M поворотом на угол 60 o . Поэтапно с помощью слайда 20 прорабатывается построение точки M₁.

— Какие инструменты нам понадобятся для того, чтобы выполнить поворот? (линейка, циркуль, транспортир)

— Ребята, что сначала нужно отметить? (точку M и центр поворота – точку O)

— Как задаём центр поворота? Отмечаем в определённом месте? (нет, произвольно)

— Как будем выполнять поворот по часовой или против часовой стрелки? Почему? (против, т.к. угол положительный)

— Что нужно построить, чтобы отложить угол 60 o ? (луч OM)

— Как найти на второй стороне угла точку M₁? (с помощью циркуля отложить отрезок OM₁=OM)

— Рассмотрим, как выполняется поворот отрезка в зависимости от расположения центра поворота.

— Рассмотрим случай, когда центр поворота лежит вне отрезка. Решим № 1166 (а). (Если класс сильный, то можно вместе с детьми составить план решения задачи, дать задание решить № 1166 (а) самостоятельно. Решение проверить с помощью СЛАЙДА 21. Если ребята затрудняются с выполнением задания, то решать коллективно, опираясь на СЛАЙД 21)

Работа в парах.

Задание. Построить фигуру, которая получится при повороте отрезка AB на угол — 100 o вокруг точки А.

— Какая точка является центром поворота? Что можно о ней сказать? (это один из концов отрезка – точка А, она будет неподвижной, оставаться на месте)

— Как будем выполнять поворот по часовой стрелки или против часовой? (по часовой, т.к. угол отрицательный)

— Составьте план решения задачи.

Задание выполняют по парам. Проверяют решение с помощью СЛАЙДА 22.

Индивидуальная работа.

Задание. Построить фигуру, в которую переходит отрезок AB при повороте на угол – 100 o вокруг точки О – середины отрезка AB.

— Составьте план решения задачи. Задание выполняют самостоятельно, решение проверяем с помощью СЛАЙДА 23.

— Сегодня на уроке мы рассмотрели поворот отрезка в зависимости от расположения центра поворота. На следующих уроках мы рассмотрим повороты других фигур. (продемонстрировать СЛАЙДЫ 24-25)

VI. Проверка усвоения изученного материала.

Тест №2. (СЛАЙДЫ 26-30)

VII. Подведение итога урока. (рефлексия)

— Ребята, давайте выделим тех, кто был лучшим на каждом этапе. (подводится итог, выставляются оценки)

— Поднимите руки, кому понравился урок. Отметьте, что интересного было на уроке?

VII. Домашнее задание.

№ 1166 (б), № 1167 – для тех, кто получил оценку “3”.
№ 1167 (рассмотреть три случая расположения центра поворота: центр — вершина А, центр расположен вне треугольника, центр лежит на стороне АВ треугольника) – для тех, кто получил оценку “4” и “5”.