В ромб вписана окружность радиусом 12

В ромб ABCD вписана окружность радиуса 12. Она касается стороны BC в точке P, при этом CP:PB=9:16. Отыскать площадь ромба

• Кирюха Зарицкий
• Геометрия 2019-03-28 16:03:45 0 1

Пусть коэффициент пропорциональности равен х. Тогда CP = 9x; PB=16x.

Пусть ABCD — ромб, О — точка пересечения диагоналей AC и BD; OP = 12.

Видео:№698. Сумма двух противоположных сторон описанного четырехугольника равна 12 см, а радиусСкачать

Сборник задач. Повторение курса геометрии 7-9 классов
материал для подготовки к егэ (гиа) по геометрии (9 класс) на тему

В сборнике собраны задачи по всем темам курса планиметрии для подготовки к ОГЭ

Видео:Геометрия В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найти радиусСкачать

Скачать:

Видео:Деление окружности на 12 равных частейСкачать

Предварительный просмотр:

Повторение курса планиметрии 7 – 9 класса

1. Сумма гипотенузы и одного катета равны 16, сумма гипотенузы и другого катета равна 18. Найдите стороны треугольника.
2. Основание равнобедренного треугольника 30 см, высота, опущенная на боковую сторону, равна 24 см. Найдите боковую сторону.
3. В равнобедренном треугольнике основание равно 80 см, высота 30 см. Определите высоту, опущенную на боковую сторону.
4. Из точки вне прямой проведены к этой прямой две наклонные и перпендикуляр. Сумма наклонных равна 56 см, а их проекции равны 8 см и 36 см. Определите перпендикуляр.
5. Медианы катетов прямоугольного треугольника равны . Найдите катеты и площадь этого треугольника.
6. Площадь прямоугольного треугольника, вписанного в круг, равна 24 см 2 , а один из катетов на 2 см больше другого. Найдите площадь круга.
7. В равнобедренную трапецию вписана окружность, диаметр которой равен 15 см. Боковая сторона трапеции равна 17 см. Найдите верхнее и нижнее основания.
8. Вычислите площадь трапеции, параллельные стороны которой равны 16см и 44см, а непараллельные равны 17см и 25см.
9. Сторона ромба равна 10 см, а его диагонали относятся как 3:4. Найдите радиус вписанной окружности.
10. Периметр ромба равен 40 см, сумма его диагоналей равна 28 см. Найдите площадь ромба.
11. Сторона квадрата, вписанного в окружность, равна 4 см. Вычислите площадь одного из отсекаемых сегментов.
12. Один из катетов прямоугольного треугольника равен 15 см, проекция другого катета на гипотенузу равна 16 см. Найдите второй катет.
13. Около круга, радиус которого равен 12 см, описана равнобокая трапеция с боковой стороной 25 см. Найдите основания трапеции.
14. В ромбе одна из диагоналей равна стороне и равна 4 см. Определите углы ромба и его площадь.
15. В треугольнике АВС сторона АВ равна 13 см, ВС=15 см, АС=14 см. Определите площадь треугольника между высотой и биссектрисой, проведенной к АС.
16. В ромб вписана окружность, радиус которой равен 12 см. Найдите сторону ромба, если его большая диагональ равна 40 см.
17. Перпендикуляр, проведенный из вершины параллелограмма на диагональ, делит её на отрезки 6 см и 15 см. Разность сторон параллелограмма равна 7 см. Найти стороны и площадь параллелограмма.
18. Дан равнобедренный треугольник с боковой стороной ВС=4 см и с медианой, опущенной на боковую сторону, равной 3 см. Найдите основание.
19. В треугольнике АВС сторона АС=60 см; высота, опущенная из вершины В равна 12 см; медиана, проведенная из точки В, равна 13 см. Определите сторону АВ, если АВ>ВС.
20. Из точки окружности, радиус которой равен 34 см, проведен к радиусу перпендикуляр, который поделил его в отношении 8:9, считая от центра. Найдите длину перпендикуляра.
21. Около равнобокой трапеции описана окружность. Диагональ трапеции перпендикулярна боковой стороне. Радиус окружности равен 10 см. Верхнее основание – 12 см. Найдите боковую сторону и диагональ.
22. Большее основание равнобокой трапеции равно 21 см, боковая сторона 10 см, диагональ – 17 см. Найдите площадь трапеции.
23. В прямоугольную трапецию с острым углом 30° и наклонной боковой стороной 4 см вписан круг. Определите отношение площади вписанного круга к площади трапеции.
24. Высота ромба 12 см, одна из его диагоналей равна 15 см. Найдите площадь ромба.
25. В круге, радиус которого равен 4 см, проведена хорда АВ так, что сумма длины хорды и расстояние от точки В до касательной, проходящей через точку А, равна 6 см. Найдите длину хорды.
26. В прямоугольный треугольник со сторонами а=6 см и b=12 см вписан квадрат, две стороны которого совпадают с катетами, а одна из вершин лежит на гипотенузе. Найдите длину стороны квадрата.
27. В прямоугольном треугольнике середина одного катета удалена от гипотенузы на 6 см, а середина гипотенузы удалена от этого же катета на 7,5 см. Найдите этот катет.
28. В равнобокой трапеции с острым углом 60° сумма оснований равна 86 см, боковая сторона – 22 см. Найдите основания трапеции.
29. Высота AD равнобедренного треугольника АВС делит боковую сторону ВС на отрезки СD=2 и DB=3, считая от основания. Определите высоту DE треугольника АВD.
30. Найдите площадь круга, описанного около равнобедренного треугольника с высотой 4 см и основанием 6 см.
31. Дан равнобедренный треугольник с основанием АС= 16 см и боковой стороной АВ=10см. Определите радиус вписанной и радиус описанной окружностей.
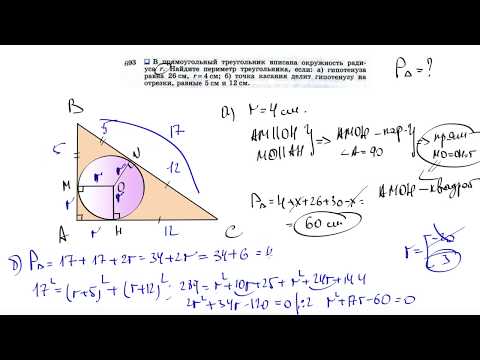
32. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5см и 12см. Найдите катеты.
33. Периметр прямоугольного треугольника равен 36см, а стороны относятся как 5:4:3. Вычислите площадь описанного круга.
34. Из точки, взятой на окружности, проведены две взаимно перпендикулярные хорды. Отрезок, соединяющий середины этих хорд, равен 12 см. Найдите длину окружности.
35. Касательная к окружности образует с хордой угол 60°. Найдите площадь круга, если известно, что хорда равна 6 см.
36. В трапеции два угла прямые. Основания равны 4см и 6см. Найти площадь вписанного в трапецию круга.
37. Дано: ABCD – трапеция, AB=CD=c, r – радиус вписанной окружности. Найдите площадь трапеции.
38. Дано: ABCD – трапеция, BD=6, средняя линия KL=7,5, ∆ АВС АСD. Найдите AD и ВС.
39. Из вершины тупого угла В ромба АВСD опущены перпендикуляры ВЕ и ВF на стороны АD и DС, пересекающие диагональ АС в точках М и N. Точка Е соединена с точкой F. Определите площадь MNFE, если диагонали ромба равны 160 и120.
40. Две параллельные хорды равны 14см и 40см, а расстояние между ними 39см. Найти площадь круга.
41. К двум касающимся окружностям проведена общая внешняя касательная, которая пересекается с продолжением линии центров в точке, удаленной от центров на 24 и 72. Определите радиусы.
42. В прямоугольном треугольнике АВС СМ и АD – медианы, СМ= и АD= . Найдите гипотенузу АС.
43. Катеты прямоугольного треугольника равны 3 и 4. Найдите расстояние между центрами вписанной и описанной окружностей.
44. В равнобокой трапеции отношение оснований равно 0,75. Средняя линия трапеции равна её высоте и равна 7см. Вычислите радиус окружности, описанной около трапеции.
45. В сегмент круга с хордой, равной 6см, вписан квадрат. Сторона квадрата 2 см. Найдите радиус круга.
46. Дан равносторонний треугольник со стороной 6 см. В него вписан равносторонний треугольник, площадь которого в 3 раза меньше площади данного треугольника. Определите расстояние между вершинами (смежными) этих треугольников.
47. Дан прямоугольный треугольник. Найдите гипотенузу, если R – радиус вписанной окружности, — угол.
48. Дан равнобедренный треугольник АВС с углом при вершине α и площадью S. Найдите высоту h.
49. Сумма оснований АD и ВС равнобокой трапеции равна 16 см, боковая сторона равна 3 см, . Вычислите: а) площадь трапеции; б) расстояние от вершины В до диагонали АС.
50. Основания равнобокой трапеции 4см и 6см. Найдите радиус вписанной окружности.

Видео:4K Как вписать окружность в ромб, видео 2023-2024 годСкачать

Нахождение радиуса вписанной в ромб окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Видео:Радиус вписанной в ромб окружности (6701)Скачать

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

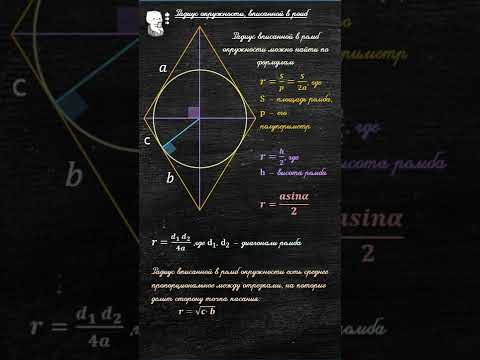
Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

• d₁ и d₂ – диагонали ромба;
• a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

Видео:Радиус и диаметрСкачать

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:

🌟 Видео

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Геометрия В ромб, который делится своей диагональю на два равносторонних треугольника, вписанаСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Построение 12 угольника циркулемСкачать

Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Школа для родителей. Циркуль, окружность, радиус, диаметр.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ОКРУЖНОСТЬ (радиус окружности, вписанной в ромб) ЧАСТЬ 11Скачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать