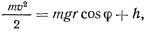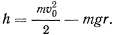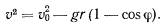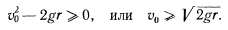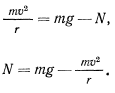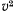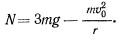Вдоль цеха по рельсам с постоянной скоростью 0,1 м/с перемещается мостовой кран АВ, по которому с постоянной скоростью 0,2 м/с движется тележка М. Определить абсолютную скорость тележки.
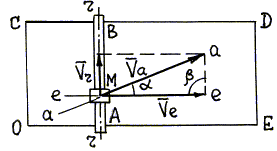 Рис. 4.14. Рис. 4.14. | 1. На расчетной схеме (рис. 4.14) изображена точка М (тележка), совершающая сложное движение и подвижное тело – кран АВ в заданный момент времени. 2. Результаты анализа сложного движения тележки (пример 1): |
- относительное движение – движение тележки М по крану АВ;
- переносное движение – движение крана АВ относительно цеха ОСDE;
- абсолютное движение – движение тележки М относительно цеха.
3. Проводим через точку М линии скоростей. Траектория относительного движения точки М – прямая АВ, поэтому линия r–r совпадает с АВ; переносным движением является поступательное движение крана вдоль стороны ОЕ цеха, поэтому линия e–e проведена параллельно OE; траекторию абсолютного движения точки М установить по условию задачи нельзя, поэтому линию а–а проводим под некоторым углом a к линии е–е, считая a искомой величиной.
4. Построим параллелограмм скоростей: по условию задачи известны направления относительной скорости точки (она равна скорости движения тележки по крану) и переносной скорости (она равна скорости точки крана, с которой в данный момент совпадает тележка); откладываем от точки М по линии r–r вектор относительной скорости` Vr, а по линии е–е – вектор переносной скорости ` Vе; затем достраиваем параллелограмм скоростей.
5. По условию задачи имеем Vr = 0,2 м/с, Vе = 0,1 м/с, угол b = 90° .
6. Решая треугольник Меа (рис. 4.14), находим
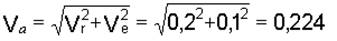

Задача 4.2
По трубке, изогнутой в форме окружности радиуса R = 20 см (рис. 4.15), течет жидкость с постоянной относительно трубки скоростью 40 см/с. Трубка вращается вокруг оси О с постоянной угловой скоростью w = 1 1/с. Найти абсолютную скорость частицы жидкости, когда она занимает в трубке положение, определяемое углом ОСМ, равным 120° . Направления вращения трубки и течения жидкости (по трубке) – против хода стрелки часов.
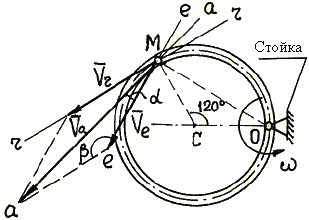 Рис. 4.15. Рис. 4.15. | 1. Расчетная схема с указанием частицы М жидкости в заданном положении изображена на рис. 4.15. 2. Результаты анализа сложного движения частицы М (пример 2):
|
3. Проводим через точку М линии скоростей: траектория относительного движения точки М – окружность с центром в точке С, поэтому линия r–r проведена по касательной к этой окружности; переносным движением здесь является вращение трубки вокруг оси О, поэтому линия е–е проведена перпендикулярно ОМ, т.е. по направлению скорости точки М’ трубки; траекторию абсолютного движения точки М здесь, как и в задаче 4.1, заранее установить нельзя, поэтому линию а–а проводим под углом a к линии е–е, считая a искомой величиной.
4. Построение параллелограмма скоростей: по условию задачи известны направления` Vr (` Vr – скорость движения по трубке) и` Vе (` Vе – скорость точки М’ трубки), откладываем от точки М векторы ` Vr и` Vе по линиям r–r и e–e; затем достраиваем параллелограмм скоростей.
5. Предварительные вычисления: по условию задачи имеем Vr = 40 см/с, модуль переносной скорости определяем по формуле
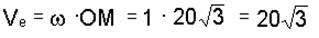
из схемы на рис. 4.15 следует, что b = 150° .
6. Решая треугольник Mea, находим
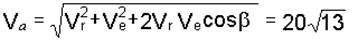
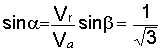
Задача 4.3
На неподвижную проволочную окружность радиуса20 см надето колечко М (рис. 4.16); через него проходит стержень ОА, который вращается вокруг оси О против часовой стрелки с угловой скоростью w = 1 1/с. Найти относительную, переносную и абсолютную скорости колечка М в момент, когда угол ОСМ равен 90° .
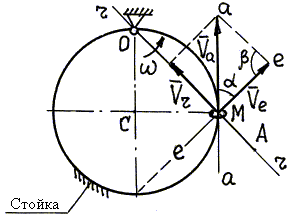 Рис. 4.16. Рис. 4.16. | 1. Расчетная схема с указанием колечка М в заданном положении (угол ОСМ равен 90° ) изображена на рис. 4.16. 2. Результаты анализа сложного движения колечка М (пример 3):
|
3. Проводим через точку М линии скоростей: линия r–r проведена вдоль ОА – траектории относительного движения; линия е–е проведена перпендикулярно ОА, – так направлена скорость точки М’ стержня ОА (переносная скорость` Ve); траектория абсолютного движения колечка М – окружность с центром в точке С, поэтому линия а–а проведена по касательной к этой окружности.
4. Построение параллелограмма скоростей: по условию задачи известно направление` Ve (` Ve – скорость точки М’ стержня ОА), откладываем ее от точки М по линии е–е; далее достраиваем параллелограмм скоростей, чтобы` Vа была диагональю.
5. Предварительные вычисления: по условию задачи определяем
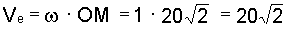
из схемы на рис. 4.16 следует, что a = 45° , b = 90° .
6. Решая треугольник Меа, находим 
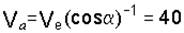
Задача 4.4
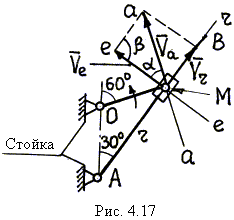 | В кулисном механизме (рис. 4.17) при вращении кривошипа ОМ вокруг оси О ползун М, перемещаясь вдоль стержня АВ, приводит этот стержень во вращательное движение вокруг оси А. Для положения механизма, изображенного на рисунке, определить скорость перемещения ползуна М по стержню АВ и угловую скорость стержня АВ, если угловая скорость кривошипа ОМ w ОМ = 2 1/с, длина кривошипа ОМ равна 10 см. Кривошип вращается против часовой стрелки. |
1. Расчетная схема механизма изображена на рис. 4.17.
2. Результаты анализа сложного движения ползуна М (пример 4):
- относительное движение – движение ползуна М по стержню АВ;
- переносное движение – вращение стержня АВ вокруг оси А стойки;
- абсолютное движение – движение ползуна М относительно стойки по окружности радиуса ОМ.
3. Проводим через точку М линии скоростей: линия r–r проведена вдоль АВ, т.е. по траектории относительного движения ползуна М; линия е–е проведена перпендикулярно АВ – так направлена скорость точки М’ стержня АВ (или переносная скорость); линия а–а проведена перпендикулярно ОМ, что соответствует направлению касательной к окружности радиуса ОМ – траектории абсолютного движения ползуна М.
4. Построение параллелограмма скоростей: по условию задачи известно направление` Vа, откладываем ее от точки М по линии а–а. Далее достраиваем параллелограмм скоростей, в котором` Vа – диагональ.
5. Предварительные вычисления: по условию задачи определяем
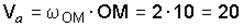
из схемы на рис. 4.17 следует a = 30° , b = 90° .
6. Решая треугольник Меа, находим
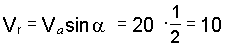
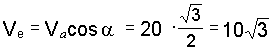
После этого определяем угловую скорость стержня АВ
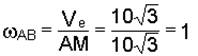
Задача 4.5
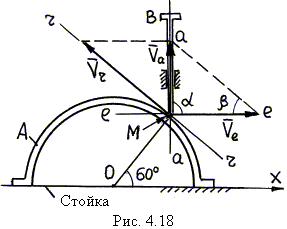 | Кулачок А (рис. 4.18), перемещаясь по горизонтальной плоскости вдоль оси х, приводит в движение толкатель ВМ, скользящий в вертикальных направляющих. Определить скорость толкателя в вертикальных направляющих в положении механизма, изображенного на рис. 4.18, если в этот момент скорость кулачка равна 30 см/с. |
1. Расчетная схема изображена на рис. 4.18.
2. Результаты анализа сложного движения точки М (см. пример 5):
- относительное движение – движение точки М по поверхности кулачка А;
- переносное движение – движение кулачка А относительно стойки;
- абсолютное движение – движение точки М относительно стойки по вертикали.
3. Проводим через точку М линии скоростей: линия r–r проведена по касательной к поверхности кулачка или иначе – по касательной к траектории относительного движения; линия e–e проведена параллельно оси х – так направлена скорость точки кулачка, с которой в данный момент совпадает конец М толкателя ВМ (или переносная скорость` Vе); линия а–а проведена по вертикали – по траектории абсолютного движения.
4. Построение параллелограмма скоростей: по условию задачи известно направление` Vе, откладываем ее от точки М по линии е–е; далее достраиваем параллелограмм скоростей, в котором` Vа – диагональ.
5. По условию задачи имеем Vе = 30 см/с. Из схемы на рис. 4.18 следует, что a = 90° , b = 30° .
6. Решая треугольник Меа, находим искомую скорость толкателя
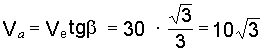
Задача 4.6
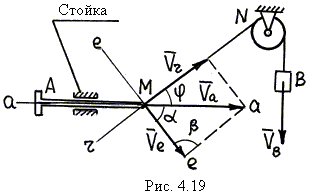 | В механизме на рис. 4.19 определить зависимость между скоростью штока АМ и скоростью опускания груза В (угол j задан). Решение 1. Расчетная схема изображена на рис. 4.19. 2. Результаты анализа сложного движения точки М (см. пример 6): |
- относительное движение – движение точки М вдоль троса МN;
- переносное движение – вращение троса MN вокруг точки N;
- абсолютное движение – движение точки М относительно стойки по горизонтали.
3. Проводим через точку М линии скоростей; линии а–а и r–r совпадают с прямолинейными траекториями абсолютного и относительного движений; линия е–е проведена перпендикулярно MN – так направлена скорость точки M’ троса в переносном вращательном движении вокруг N.
4. Построение параллелограмма скоростей: по условию задачи известно направление скорости` VВ (вниз), для точки М это соответствует заданию` Vr; откладываем` Vr по линии r–r, а затем достраиваем параллелограмм скоростей, в котором` Va – диагональ.
5. Из схемы на рис. 4.19 следует, что a = 90° – j , b = 90° .
6. Решая треугольник Меа, находим
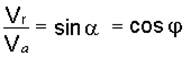
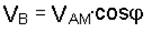
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

На проволочной окружности радиуса
2018-03-18 
Бусинка массой $m$ надета на гладкое проволочное кольцо радиусом $R$, плоскость которого наклонена под углом $30^$ к горизонту. Кольцо жесткое и закреплено неподвижно. Какая сила действует со стороны кольца на бусинку в момент прохождения ею нижнего положения, если бусинка соскользнула без начальной скорости из верхней точки?
Напишем 2-й закон Ньютона для бусинки:
где $vec$ — сила, действующая со стороны кольца, $vec$ — ускорение свободного падения. В нижней точке ускорение бусинки направлено к центру кольца, так как тангенциальное ускорение здесь равно нулю. Проектируя векторное уравнение на оси x (направленную по диаметру кольца) и y (перпендикулярную плоскости кольца), см. рис., выражаем компоненты силы $vec$:
$N_ = m frac <V^> + mg sin alpha$,
$N_ = mg cos alpha$.
Скорость бусинки в нижней точке найдем из закона сохранения энергии (трения нет):
$V^ = 2g(2R sin alpha)= 4gR sin alpha$.
Подставляя $V^$ в выражение для $N_$ и учитывая, что $alpha = 30^$, имеем для $N$:
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Тяжелое колечко массы надето на гладкую вертикально расположенную проволочную окружность радиуса
Задача №50.
Тяжелое колечко массы 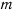
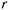
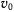
Решение:
На точку действует только одна активная сила — сила тяжести 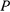
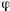
где 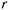
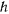
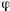
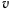
Тогда для скорости точки получим уравнение
Чтобы колечко совершило полный оборот, скорость в верхней точке окружности должна быть отлична от нуля. Отсюда получаем условие для определения начальной скорости точки
Давление колечка в верхней точке окружности определится из уравнения
Таким образом, будем иметь после подстановки
Здесь положительное значение реакция 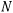
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Возможно эти дополнительные задачи вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📽️ Видео
Длина окружности. Математика 6 класс.Скачать

КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте СегментаСкачать

Радиус описанной окружностиСкачать

КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Физика - движение по окружностиСкачать

Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Найти центр и радиус окружностиСкачать

КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

+Как найти длину окружностиСкачать

Дистанционный урок по Технологии - "Технология работы с проволокой".Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать