Стереометрия изучает фигуры в пространстве. Наше пространство трехмерно, в нем есть три измерения — это длина, ширина и высота. Однако это не значит, что все окружающие нас тела имеют три измерения. Плоские фигуры имеют только два измерения, но также могут рассматриваться в стереометрии. Хотя стереометрия обычно акцентируется на объемных (трехмерных) телах.
Объемные тела называются геометрическими телами. У таких тел есть поверхности, которые отделяют их от окружающего пространства. Эти поверхности представляют собой плоские фигуры. Например, куб — это объемное тело, его поверхность состоит из шести квадратов. Шар — объемное тело, его поверхность — сфера.
Поверхности многих геометрических тел (но не всех) являются многоугольниками (четырехугольниками, шестиугольниками, треугольниками и др.). Здесь под многоугольником понимается фигура, состоящая из сторон и ограниченной ими внутренней области. Поверхность, состоящую из многоугольников (или фигуру, чья поверхность состоит из многоугольников), называют многогранником.
Поверхности многогранника называют гранями. По-сути грани представляют собой плоскости, ограниченные сторонами многоугольников, из которых состоит многогранник. Сами стороны многоугольников называются ребрами. По-сути они представляют собой отрезки. Концы ребер соединены между собой, эти точки соединения называют вершинами многогранника.
Также в многогранниках выделяют диагонали. Это отрезки, которые соединяют вершины разных граней.
- Треугольник
- Типы треугольников
- По величине углов
- Остроугольный треугольник
- Тупоугольный треугольник
- Прямоугольный треугольник
- По числу равных сторон
- Разносторонний треугольник
- Равнобедренный треугольник
- Равносторонний (правильный) треугольник
- Вершины, углы и стороны треугольника
- Свойства углов и сторон треугольника
- Сумма углов треугольника равна 180°
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Формулы сторон через медианы
- Медианы треугольника
- Свойства медиан треугольника
- Формулы медиан треугольника
- Формулы медиан треугольника через стороны
- Биссектрисы треугольника
- Свойства биссектрис треугольника
- Формулы биссектрис треугольника
- Формулы биссектрис треугольника через стороны
- Формулы биссектрис треугольника через две стороны и угол
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Формулы высот треугольника через сторону и угол
- Формулы высот треугольника через сторону и площадь
- Формулы высот треугольника через две стороны и радиус описанной окружности
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
- Радиус вписанной в треугольник окружности через три стороны
- Формулы высот треугольника через две стороны и радиус описанной окружности
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Свойства углов
- Формулы радиуса окружности описанной вокруг треугольника
- Радиус описанной окружности через три стороны и площадь
- Радиус описанной окружности через площадь и три угла
- Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
- Связь между вписанной и описанной окружностями треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Радиус описанной окружности через площадь и три угла
- Средняя линия треугольника
- Свойства средней линии треугольника
- Признаки
- Периметр треугольника
- Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
- Формула площади треугольника по трем сторонам
- Формула площади треугольника по двум сторонам и углу между ними
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
- Равенство треугольников
- Определение
- Свойства
- Признаки равенства треугольников
- По двум сторонам и углу между ними
- По стороне и двум прилежащим углам
- По трем сторонам
- Подобие треугольников
- Определение
- Признаки подобия треугольников
- Свойства
- Прямоугольные треугольники
- Свойства прямоугольного треугольника
- Признаки равенства прямоугольных треугольников
- Свойства
- Тетраэдр
- Поэтому на вопрос — «что такое тетраэдр?», можно дать следующее определение: » Тетраэдр это геометрическое тело из четырех граней, каждая их которых — правильный треугольник «.
- Математические характеристики тетраэдра
- Вариант развертки
- Видео. Тетраэдр из набора «Волшебные грани»
- Видео. Вращение всех правильных многогранников
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

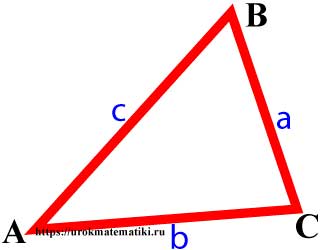
Треугольник
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Типы треугольников
По величине углов
Остроугольный треугольник
— все углы треугольника острые.
Тупоугольный треугольник
— один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник
— один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник
— все три стороны не равны.
Равнобедренный треугольник
— две стороны равны.
Равносторонний (правильный) треугольник
— все три стороны равны.
Видео:Подсчёт количества граней и рёбер у трёхмерных фигур | Фигура | ГеометрияСкачать

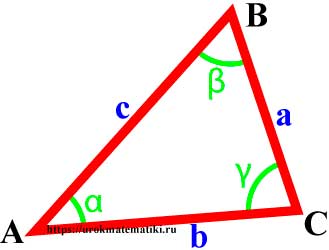
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
- если α > β , тогда a > b
- если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
a sin α = b sin β = c sin γ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 b c · cos α
b 2 = a 2 + c 2 — 2 a c · cos β
c 2 = a 2 + b 2 — 2 a b · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a = 2 3 2 m b 2 + m c 2 — m a 2
b = 2 3 2 m a 2 + m c 2 — m b 2
c = 2 3 2 m a 2 + m b 2 — m c 2
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Медианы треугольника
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AO OD = BO OE = CO OF = 2 1
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников
S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE
Формулы медиан треугольника
Формулы медиан треугольника через стороны
m a = 1 2 2 b 2 + 2 c 2 — a 2
m b = 1 2 2 a 2 + 2 c 2 — b 2
m c = 1 2 2 a 2 + 2 b 2 — c 2
Видео:Виды треугольниковСкачать

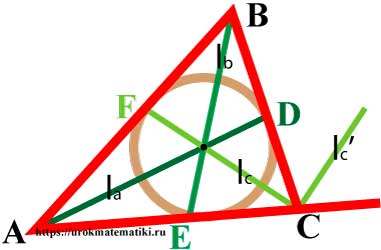
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника
- Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AE AB = EC BC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°
Угол между l c и l c ‘ = 90°
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
l a = 2 b c p p — a b + c
l b = 2 a c p p — b a + c
l c = 2 a b p p — c a + b
где p = a + b + c 2 — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
l a = 2 b c cos α 2 b + c
l b = 2 a c cos β 2 a + c
l c = 2 a b cos γ 2 a + b
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

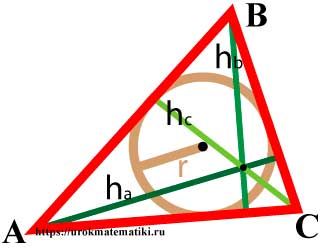
Высоты треугольника
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
1 h a : 1 h b : 1 h c = 1 r
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
h a = b sin γ = c sin β
h b = c sin α = a sin γ
h c = a sin β = b sin α
Формулы высот треугольника через сторону и площадь
Формулы высот треугольника через две стороны и радиус описанной окружности
Видео:Задача. Сколько вершин граней и ребер у многогранника?Скачать

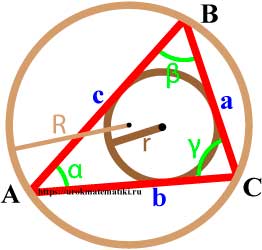
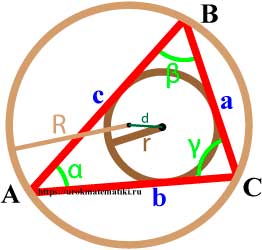
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
Радиус вписанной в треугольник окружности через три стороны
Формулы высот треугольника через две стороны и радиус описанной окружности
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

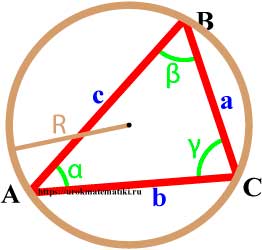
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
- Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
- Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
Радиус описанной окружности через площадь и три угла
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
Видео:Построение натуральной величины треугольника методом вращенияСкачать

Связь между вписанной и описанной окружностями треугольника
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
d 2 = R 2 — 2 R r
Радиус описанной окружности через площадь и три угла
Видео:ЗАРАБОТАЙ на ПЛОХИХ НОВОСТЯХ из АМЕРИКИ. Форекс обзор 22.01.2024Скачать

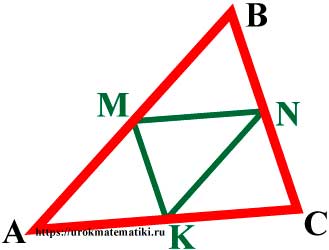
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
- Любой треугольник имеет три средних линии.
- Средняя линия треугольника параллельна основанию и равна его половине.
MN = 1 2 AC ; KN = 1 2 AB ; KM = 1 2 BC
MN || AC ; KN || AB ; KM || BC
S ∆MBN = 1 4 S ∆ABC ; S ∆MAK = 1 4 S ∆ABC ; S ∆NCK = 1 4 S ∆ABC
∆MBN
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S = 1 2 a · h a ,
S = 1 2 b · h b ,
S = 1 2 c · h c ,
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
S = 1 2 b · c · sin α ,
S = 1 2 a · c · sin β ,
где a, b, c — стороны треугольника,
γ — угол между сторонами a и b ,
α — угол между сторонами b и c ,
β — угол между сторонами a и c .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Видео:Треугольники. 7 класс.Скачать

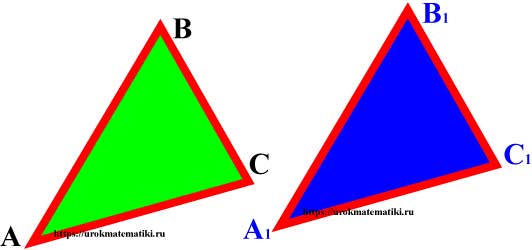
Равенство треугольников
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Видео:№238. Докажите, что в равнобедренном треугольнике отрезок, соединяющий любую точку основания,Скачать

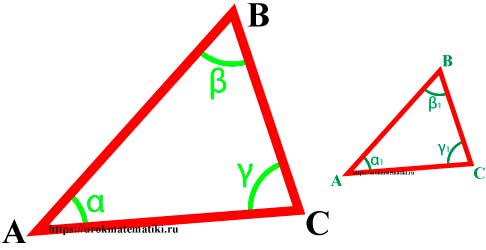
Подобие треугольников
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
∆MNK => α = α 1 , β = β 1 , γ = γ 1 и AB MN = BC NK = AC MK = k
где k — коэффициент подобия.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S ∆АВС S ∆MNK = k 2
Видео:Уравнения стороны треугольника и медианыСкачать

Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∠ 1 + ∠ 2 = 90° .
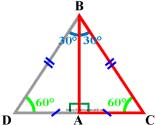
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.
Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.
Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Тетраэдр
Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» — означает грань (тетраэдр – четырехгранник).
Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Поэтому на вопрос — «что такое тетраэдр?», можно дать следующее определение: » Тетраэдр это геометрическое тело из четырех граней, каждая их которых — правильный треугольник «.
Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .
Тетраэдр имеет следующие характеристики:
- Тип грани – правильный треугольник;
- Число сторон у грани – 3;
- Общее число граней – 4;
- Число рёбер, примыкающих к вершине – 3;
- Общее число вершин – 4;
- Общее число рёбер – 6;
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.
Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.
Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.
Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Математические характеристики тетраэдра
Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы тетраэдра определяется по формуле:
, где a — длина стороны.
Сфера может быть вписана внутрь тетраэдра.
Радиус вписанной сферы тетраэдра определяется по формуле:
Площадь поверхности тетраэдра
Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:
Объем тетраэдра определяется по следующей формуле:
Высота тетраэдра определяется по следующей формуле:
Расстояние до центра основания тетраэдра определяется по формуле:
Видео:Хитрый периметрСкачать

Вариант развертки
Тетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.
Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.
Заметим, что это не единственный вариант развертки.
Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
— если Вы предполагаете распечатать на цветном принтере — цветная развертка
— если Вы предполагаете использовать для сборки цветной картон — развертка
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Видео. Тетраэдр из набора «Волшебные грани»
Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора «Волшебные грани».
Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
вращение готового многогранника:











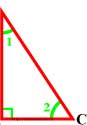 Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма двух острых углов прямоугольного треугольника равна 90°.