§ 12. Параллельное проектирование и его свойства.
В начале учебника на плоскости изображены некоторые фигуры, расположенные в пространстве. Эти изображения строились с целью придать наглядность тому, о чём шла речь в соответствующей теореме или задаче.
Однако изображения пространственных фигур на плоскости строятся по определённым правилам и в школьном курсе геометрии обычно осуществляются с помощью метода параллельного проектирования, сущность которого состоит в следующем.
В пространстве выбирается произвольная плоскость π Плоскость проекций в начертательной геометрии чаще всего обозначают π . , которую называют плоскостью проекций или плоскостью изображения , и прямая l , пересекающая эту плоскость (рис. 71, а ).
Пусть M ′ — произвольная точка пространства. Через эту точку проведём прямую p , параллельную l . Точка M пересечения прямой p с плоскостью π называется параллельной проекцией точки M ′ на плоскость π в направлении прямой l . Если M ′ — точка плоскости π , то M совпадает с M ′ .
При этом часто пользуются обозначением: M = П 
Прямую l и все прямые пространства, параллельные ей, называют проектирующими прямыми ; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью .
Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, её определяющих. На рисунке 71, б треугольник ABC является параллельной проекцией треугольника A ′ B ′ C ′ на плоскость π в направлении прямой l .
Замечание. Наряду с параллельным проектированием рассматривается также центральное проектирование фигур на плоскость. В этом случае проектирующие прямые проходят через одну точку — центр проектирования , произвольно выбранную вне плоскости проекций (рис. 71, в ).
Параллельное и центральное проектирование можно наблюдать в реальном пространстве: тень, которую отбрасывает предмет в солнечный день, является параллельной проекцией этого предмета, так как солнечные лучи можно считать приближённо параллельными вследствие большого удаления Солнца от Земли. А изображение на экране кинотеатра фигуры, заснятой на киноплёнку, является центральной проекцией этой фигуры.
На рисунках 72, 73, 74 изображены в параллельной проекции соответственно квадрат, треугольник и каркас тетраэдра. По этим рисункам можно сделать предположение, что ни величина угла, ни длина отрезка при параллельном проектировании, вообще говоря, не сохраняются.
Рассмотрим некоторые свойства параллельного проектирования.
1. Все точки проектирующей прямой проектируются в одну точку — точку пересечения этой прямой с плоскостью проекций (рис. 75).
В дальнейшем мы будем рассматривать проекции прямых, не параллельных проектирующим прямым.
2. Проекция прямой есть прямая. Действительно, все прямые, проектирующие точки данной прямой m ′ (рис. 76), принадлежат некоторой проектирующей плоскости, которая пересекает плоскость проекций по некоторой прямой m — параллельной проекции прямой m ′ .
Причём, так как через точку, не лежащую на данной прямой, можно провести лишь одну прямую, параллельную этой прямой (т. 6) (мы проводим прямые, параллельные прямой l ), то каждая точка прямой m ′ проектируется в единственную точку своей проекции — прямой m , и наоборот, каждая точка прямой m является проекцией единственной точки прямой m ′ .
Из доказательства этого свойства следует: три точки, лежащие на одной прямой, проектируются в три точки, также лежащие на одной прямой .

3. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Действительно, если прямые a ′ и b ′ лежат в одной проектирующей плоскости, то они проектируются в одну и ту же прямую, а именно, в прямую, по которой эта проектирующая плоскость пересекает плоскость проекций.
Пусть теперь прямые a ′ и b ′ параллельны (рис. 77) и не лежат в одной проектирующей плоскости.
Обозначим через α и β плоскости, образованные прямыми, проектирующими точки прямых соответственно a ′ и b ′ . Прямые a и b , по которым плоскости α и β пересекают плоскость проекции, не могут пересекаться, так как если бы эти прямые имели общую точку M , то и прямые a ′ и b ′ по свойству 2 имели бы общую точку M ′ , что невозможно в силу параллельности прямых a ′ и b ′ . А так как прямые a и b лежат в одной плоскости (плоскости проекций) и не имеют общей точки, то они параллельны, т. е. параллельными проекциями параллельных прямых, не лежащих в одной проектирующей плоскости, являются параллельные прямые.
Заметим, что плоскости α и β , проектирующие параллельные прямые a ′ и b ′ , не лежащие в одной проектирующей плоскости, параллельны (в п. 9.1 показано, что параллельные плоскости существуют; о свойствах параллельных плоскостей речь пойдёт в следующей главе).
4. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков.
Если отрезки A ′ B ′ и B ′ C ′ лежат на одной прямой a ′ и проектируются на отрезки соответственно AB и BC прямой a (рис. 78), то по обобщённой теореме Фалеса в плоскости, определяемой прямыми a и a ′ , получаем A ′ B ′ : B ′ C ′ = AB : BC = m : n .
Пусть теперь отрезки A ′ B ′ и C ′ D ′ расположены соответственно на данных параллельных прямых a ′ и b ′ , не лежащих в одной проектирующей плоскости, и A ′ B ′ : C ′ D ′ = m : n ; AB и CD , a и b — соответственно их параллельные проекции на плоскость π (рис. 79).
Так как a ′ ‖ b ′ , то (по свойству 3) a ‖ b . Пусть E — такая точка прямой a , что четырёхугольник BCDE — параллелограмм. Тогда на прямой a ′ существует (единственная!) такая точка E ′ , что E ′ E ‖ DD ′ и A ′ B ′ : B ′ E ′ = AB : BE . А так как BC ‖ ED , то B ′ C ′ ‖ E ′ D ′ (по свойству 3), значит, B ′ C ′ D ′ E ′ — параллелограмм. Поэтому A ′ B ′ : C ′ D ′ = A ′ B ′ : B ′ E ′ = AB : BE = AB : CD , т. е. A ′ B ′ : C ′ D ′ = AB : CD = m : n .
Из этого свойства, очень важного для теории построений изображений пространственных фигур на плоскости, следует не менее важный вывод: если отрезок A ′ C ′ параллельно проектируется на отрезок AC и точка B ′ делит отрезок A ′ C ′ в отношении A ′ B ′ : B ′ C ′ = m : n , то точка B — проекция точки B ′ — делит отрезок AC в том же отношении m : n , т. е. AB : BC = A ′ B ′ : B ′ C ′ = m : n . В частности, середина отрезка A ′ C ′ параллельно проектируется в середину отрезка AC ( m : n = 1 : 1) (рис. 80).
Пусть M — внутренняя точка отрезка AB .
Определение. Число λ , равное отношению длин отрезков AM и MB , на которые точка M делит отрезок AB , называется простым отношением трёх точек A , B и M , лежащих на одной прямой, и обозначается ( AB ; M ), т. е. ( AB ; M ) = λ = AM : MB .
При этом точки A и B называются базисными , а точка M — делящей точкой.
Упорядоченность точек простого отношения необходима. Например, если AA 1 — медиана треугольника ABC , M — его центроид (точка пересечения медиан треугольника), то ( AA 1 ; M ) = AM : MA 1 = 2 : 1, но ( A 1 A ; M ) = A 1 M : MA = 1 : 2 (рис. 81). Поэтому, если AM ≠ MA 1 , то
( AA 1 ; M ) ≠ ( A 1 A ; M ).
Учитывая свойство 4 параллельного проектирования, можно сделать вывод: простое отношение трёх точек, лежащих на одной прямой, при параллельном проектировании сохраняется . В этом случае также говорят, что простое отношение трёх точек, лежащих на одной прямой, — инвариант параллельного проектирования .
Свойства фигуры, сохраняющиеся при параллельном проектировании, называются аффинными свойствами этой фигуры. Например, свойства прямых быть параллельными — аффинное свойство этих прямых; инвариантность простого отношения трёх точек одной прямой — аффинное свойство таких точек.
Подробнее о параллельном проектировании и изображениях фигур на плоскости читайте в конце учебника.
Определение. Проектирование в направлении прямой, перпендикулярной плоскости проекций, называется ортогональным.
Удобно пользоваться обозначением: M = П 
Ортогональное проектирование является частным случаем параллельного и обладает всеми его свойствами. Однако, если при параллельном проектировании, не являющимся ортогональным, длина проекции отрезка может быть меньше, больше или равна длине самого отрезка, то при ортогональном проектировании длина проекции отрезка не больше, чем длина самого отрезка, и длины этих отрезков связаны соотношением: П 
Задания для работы с интернет-ресурсами
1. Наберите в поисковой системе слова «Перпендикулярность прямой и плоскости», «Перпендикуляр и наклонная к плоскости», «Наклонная и её проекция на плоскость», «Теорема о трёх перпендикулярах». На изображениях куба, параллелепипеда найдите рёбра и диагонали, перпендикулярные граням и сечениям этих многогранников. Найдите видеоролики с лекциями опытных педагогов и геометров, в которых выражаются различные взгляды как на теорию, так и на решение задач по этим вопросам.
2. Наберите в поисковой системе слова «угол между наклонной и плоскостью». Поищите задачи ЕГЭ типа С-2, в которых используется нахождение угла между прямой и плоскостью, посмотрите, как они решаются, попробуйте решить их самостоятельно. Если вам удалось найти в Интернете тренинг по решению задач этой темы, то попытайтесь им воспользоваться. Однако решать такие задачи целесообразнее после изучения темы «Расстояния в пространстве». Скоро вы изучите эту тему.
3. Изображения фигур на плоскости и в живописи подчиняются определённым законам. Найдите в Интернете такие имена, как Филиппо Брунеллески (1377—1446), Леонардо да Винчи (1452—1519) и Альбрехт Дюрер (1471—1528). Вы увидите творчество этих великих художников. Однако существует направление, которое называется импоссибилизм (impossibility — невозможность) — изображение невозможных фигур, парадоксов. Представителем этого направления живописи является известный голландский художник Мауриц Эшер (1898—1972). Найдите статьи, посвящённые его творчеству, а главное, найдите сами репродукции картин, которые представляют большой интерес и с точки зрения геометрии.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Школьная лекция по теме «Параллельность в пространстве» 10 класс
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Тема: «Параллельность в пространстве» Урок-лекция 10 класс
Основные определения: две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются. две плоскости называются параллельными, если они не пересекаются. плоскость и прямая называются параллельными, если они не пересекаются.
Теоремы-признаки Две прямые параллельны между собой, если они каждая параллельны третьей прямой. Если прямая, не принадлежащая плоскости параллельна какой-либо прямой в этой плоскости, то она параллельна самой плоскости. Если две пересекающихся прямых одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны между собой.
Теорема –признак параллельности прямой и плоскости. Если прямая, не лежащая в плоскости , параллельна какой-то прямой в плоскости, то она параллельна всей плоскости. Доказательство: Пусть есть прямая а в плоскости α , а вне её есть прямая в, причём а//в. Докажем , что в//α. Пусть не параллельна, тогда прямая в пересекает плоскость в некоторой точке С. Так как через две пересекающиеся прямые проходит плоскость β, то плоскость α имеет с плоскостью β общую точку С, а значит пересекается по прямой а. Тогда через точку С проходят две различные прямые, которые по предположению пересекаются, а по условию параллельны. Этого быть не может, значит, предположение не верно, и прямая а//α.
Теорема-признак параллельности плоскостей Если две пересекающихся прямых одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны между собой. Пусть плоскости пересекаются. Тогда прямая с принадлежит и плоскости α и плоскости β. Получается, что если сα, то с//а и с//в, лежащих в плоскости β , так как если прямая параллельна плоскости, тогда она параллельна любой прямой этой плоскости. Значит, через точку С проходит две различные параллельные прямые. Что является противоречием, а значит плоскость α параллельна плоскости β.
Теоремы (для построения) Через точку вне прямой можно провести прямую параллельную данной и только одну. Через точку вне плоскости можно провести плоскость параллельную данной и только одну. Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны. Отрезки параллельных прямых, заключённые между двумя параллельными прямыми равны между собой .
Изображение пространственных фигур. Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая. Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка. Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой. Свойство 4. Если плоская фигура F лежит в плоскости, параллельной плоскости проектирования π, то ее проекция F’ на эту плоскость будет равна фигуре F. Пусть F — некоторая фигура в пространстве. Проекции ее точек на плоскость α образуют фигуру F ‘, которая называется параллельной проекцией фигуры Ф на плоскость α в направлении прямой l. Говорят также, что фигура F ‘ получена из фигуры F параллельным проектированием.
Основное правило: параллельность и отношение длин сохраняется, длины отрезков и углы, не сохраняются . на основании этого правила скажите квадрат изображается? прямоугольник изображается? параллелограмм изображается? медиана изображается? высота изображается? Круг изображается овалом или эллипсом .
Из свойств параллельного проектирования следует, что параллельной проекцией многоугольника является или многоугольник с тем же числом сторон или отрезок. Причем, если в многоугольнике какие-нибудь две стороны параллельны, то их проекции также будут параллельны. При параллельном проектировании длины отрезков и углы, не сохраняются, проекцией равностороннего треугольника может быть треугольник с разной длиной сторон, проекцией прямоугольного треугольника может быть не прямоугольный треугольник. Проекцией параллелограмма является параллелограмм, проекцией прямоугольника может не быть прямоугольник, проекцией ромба не обязательно является ромб, проекцией правильного многоугольника может быть неправильный многоугольник.
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами параллелепипед куб Прямоугольный параллелепипед
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий ее основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы
Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий ее основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить ее с вершинами многоугольника. Полученные отрезки будут изображать боковые ребра пирамиды.
Упражнения 1. В каком случае параллельной проекцией прямой будет точка? Ответ: Если прямая параллельна направлению проектирования. 2. В каком случае параллельной проекцией двух параллельных прямых является одна прямая? Ответ: Если плоскость, в которой лежат эти прямые, параллельна направлению проектирования. 3. Какие фигуры могут быть параллельными проекциями двух скрещивающихся прямых? Ответ: Две пересекающиеся прямые; две параллельные прямые; прямая и точка, ей не принадлежащая. 4. Сохраняются ли при параллельном проектировании: а) длины отрезков; б) величины углов? Ответ: а), б) Нет.
5. Верно ли, что если длина отрезка равна длине его параллельной проекции, то отрезок параллелен плоскости проектирования? Ответ: Нет. 6. Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в) разносторонний треугольник? Ответ: а), б), в) Да. 7. Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция? Ответ: а), б), в) Да; г) нет. 8. Верно ли, что при параллельном проектировании треугольника: а) медианы проектируются в медианы; б) высоты проектируются в высоты; в) биссектрисы проектируются в биссектрисы? Ответ: а) Да; б), в) нет.
Параллельными проекциями каких многогранников являются фигуры, изображенные на рисунке? Ответ: а), б) 4-я пирамида; в) тетраэдр; г), д) 6-я пирамида; е) параллелепипед.
Верно ли? Для любых двух прямых можно провести плоскость, параллельную каждой из них.(нет, случай перпендикулярности прямых). Все прямые , проходящие через данную точку, параллельно данной плоскости, лежат в одной плоскости.(да). Сохраняется ли при параллельном проектировании отрезков одной плоскости их отношение?(да) Может ли при параллельном проектировании трапеции получиться прямоугольник? (нет). Может ли при параллельном проектировании параллелограмма получиться прямоугольник?(да) Может ли параллельная проекция произвольного параллелограмма быть ромбом? (нет) Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в плоскости? (нет)
Какая из указанных фигур не может быть параллельной проекцией правильного треугольника, в котором построена одна высота?
Какая из указанных фигур не может быть проекцией пространственного четырёхугольника?
Каково взаимное расположение а и в?АДα. ВС по отношению к α?
АДα..МNпо отношению к ВС?
В пространстве даны прямая и точка А. Сколько существует прямых, которые проходят через А и параллельны прямой. Через стороны АВ и СД четырёхугольника АВСД и точку К вне его проведены две плоскости , пересекающиеся по прямой параллельной каждой из прямых АВ иСД. Установите вид четырёхугольника АВСД, если известно, что АВ=СД.
С А В F N M К Дано: F ∉ АВС. FА, FВ, FС. АМ=MF, BK=FK, FN=NC. Выбрать три пары параллельных прямых. Доказать, что они параллельны.
С А В F N M К Дано:∆ АВС, F ∉ (АВС) M∈AF, K∈FB, N∈FC FM:MF=FK:KB=FN:NC Доказать, что (ABC)||(MNK)
В С С₁ В₁ А α Дано :α ∩ AB=B₁; α ∩ AC=C₁ AB₁:B₁C₁=2:3, BC=15 см, ВВ₁=6 см BC||α Найти: В₁С₁
α M N A B C D Дано : АВСD- трапеция α││АD; α∩АВ=М ,α∩ СД=N AM=MB, CN=ND. BC=9 см , AD= 17см Найти :MN
Отрезок АВ не пересекает плоскость α. Через середину отрезка С и концы отрезка А и В проведены прямые, параллельные между собой и пересекающие плоскость α в точках А1 , В1 и С1. Вычислить длину отрезка СС1, если АА1= 5, ВВ1= 7. α А В С А1 В1 С1
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

$ AlexLat $
Изображение пространственных фигур на плоскости
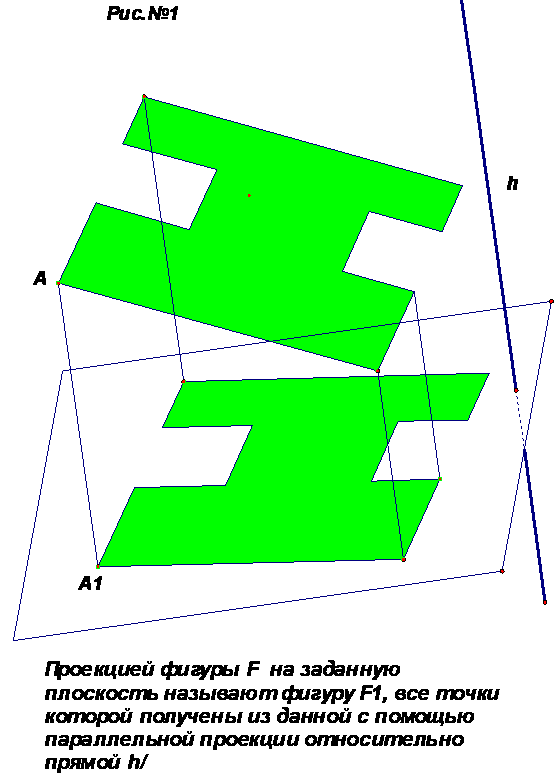
Д ля изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием (в черчении говорят «проецированием»). Этот способ изображения фигур состоит в следующем: берём произвольную прямую «h», пересекающую плоскость чертежа «α», проводим через произвольную точку А фигуры прямую, параллельную прямой «h.» Точка А1 пересечения этой прямой с плоскостью чертежа будет изображением точки А (см. рис.1)
Построим, таким образом, изображение каждой точки фигуры, получим изображение самой фигуры. Такой способ изображения пространственной фигуры на плоскости соответствует зрительному восприятию фигуры, при рассмотрении её издали.
Уточняющий вопрос к объяснению:
Может ли прямая, проведённая через точку А параллельно прямой «h» , не пересечь плоскость «α»?
Ответ: обязательно пересечёт, т.к. если плоскость пересекает одну из двух параллельных прямых, то она пересекает и другую.
Свойства параллельного проектирования.
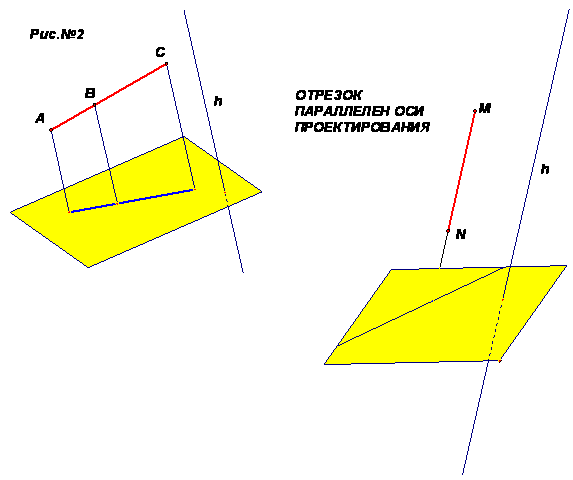
1)Чем может быть изображён отрезок на плоскости?
2)Какой фигурой может оказаться параллельная проекция отрезка?
Ответ: отрезком или точкой, если этот отрезок параллелен прямой проектирования «h».
•Таким образом: прямолинейные отрезки фигуры изображаются на плоскости чертежа отрезками (см. рис2)
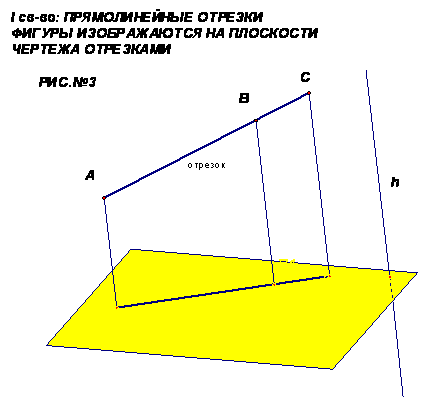
Действительно, все прямые, проектирующие точки отрезка АС, лежат в одной плоскости, пересекающей плоскость чертежа «α» по прямой А1С1. Произвольная точка В отрезка АС изображается точкой В1 отрезка А1С1.(рис.№3)
Замечание. В только что доказанном свойстве и далее предполагается, что, конечно, что проектируемые отрезки не параллельны направлению проектирования.
То есть мы показали, что проекцией каждой точки отрезка АС является точка отрезка А1С1.
Следствие I свойства:
Многогранники ( плоские или пространственные) изображаются на плоскости чертежа многогранниками (или, в исключительных случаях, отрезками)
1)Может ли при параллельном проектировании многоугольника получиться многоугольник с меньшим числом сторон?
Ответ: Да, если многоугольник пространственный.
Для плоских многоугольников ответ отрицательный (нет).
Как изобразятся при параллельном проектировании параллельные прямые (отрезки).
Ответ: параллельными или совпадающими прямыми (параллельными или лежащими на одной прямой отрез
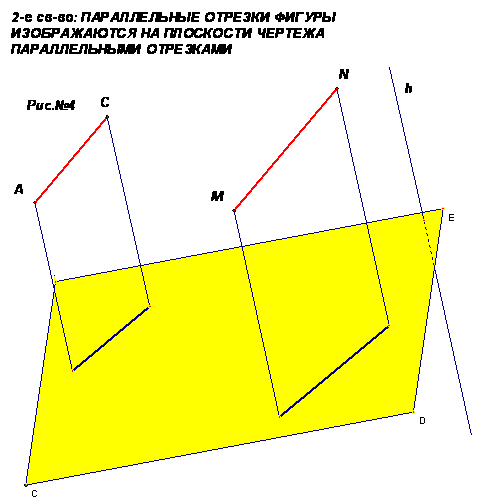
• Параллельные отрезки фигуры изображаются на плоскости чертежа параллельными отрезками (см. рис4)
Действительно, пусть АС ║ А′С′. Прямые А1С1 ║ А′1С′1 т.к. они получаются при пересечении параллельных плоскостей с плоскостью «α». Первая проходит через АС и АА1 , вторая через А′С′ и А′А′1 .
Вопрос: Почему указанные плоскости параллельны?
(если две параллельные плоскости параллельны, то линии их пересечения параллельны)
Может ли при параллельном проектировании параллелограмма получиться трапеция?
Так как при параллельном проектировании параллельные прямые изображаются параллельными, то параллельной проекцией параллелограмма будет параллелограмм (или отрезок).
1)Сохраняются ли длины отрезков при параллельном проектировании? (если отрезки параллельны плоскости, то сохраняются).
2)Сохраняются ли отношения длин?
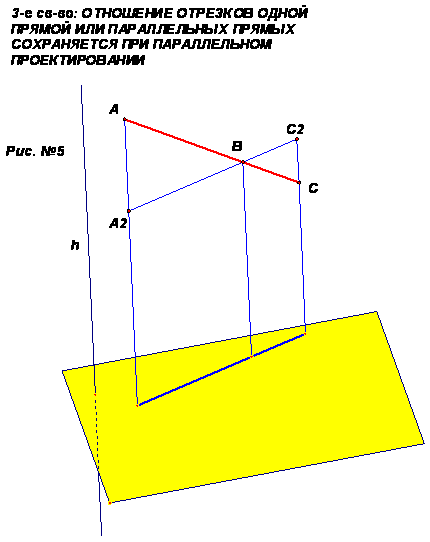
Так как мы уже достаточно поработали устно, то для доказательства третьего свойства сделаем чертёж(см. рис.№5).
• Отношение отрезков одной прямой или параллельных
прямых сохраняются при параллельном проектировании.
Рассмотреть доказательство третьего свойства по чертежу.
Дано: отрезок АС, который разделён точкой В в отношении 2:1 (считая от точки А).
Доказать, что проекция отрезка А1 С1 делится точкой В1 в отношении 2:1 (считая от точки А1)
А теперь рассмотрим задачу по готовому чертежу.
Дана параллельная проекция треугольника. Как построить проекции медиан этого треугольника
При параллельном проектировании сохраняется отношение отрезков прямой, поэтому, середина стороны треугольника проектируется в середину проекции этой стороны. Следовательно, проекции медиан треугольника будут медианами его проекций.
Эта задача имеет довольно неожиданное применение. Очевидно, в правильном (равностороннем) треугольнике медианы пересекаются в одной точке – в центре треугольника. Но произвольный треугольник АВС можно спроектировать в правильный треугольник АВС1 (см. рис).Достаточно построить такой правильный треугольник АВС1 в плоскости, не проходящей через точку С и проектировать параллельно прямой h = СС1 Рассматривая эту проекцию видим, что медианы любого треугольника пересекаются в одной точке.
Докажите, что параллельная проекция центрально — симметричной фигуры также является центрально – симметричной.
Назвать известные центрально симметричные фигуры.
Ответ: квадрат, окружность, круг.
Так как при параллельном проектировании середина отрезка переходит в середину его проекции, проекция центра симметрии фигуры будет являться центром симметрии проекции этой фигуры.
🌟 Видео
10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Параллельность прямых. 10 класс.Скачать

тема 8 3 Параллельное проектирование и его свойстваСкачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Параллельные прямые циркулемСкачать

8 класс, 19 урок, Пропорциональные отрезкиСкачать

Отношение отрезков и площадей (Задача №324623)Скачать
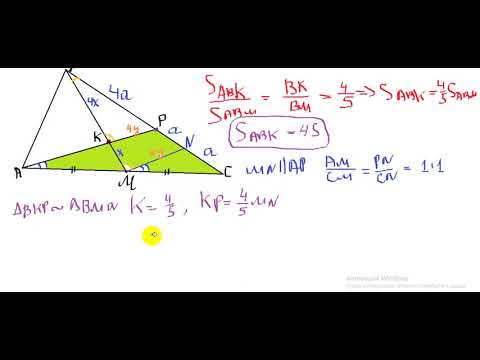
КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Занятие 7 Площадь и отношения отрезковСкачать

10. Проецирование одной прямой на другуюСкачать

Параллельное проектирование и его свойства Изображение пространственных фигурСкачать

виды проецирования и свойства параллельного проецированияСкачать
7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать