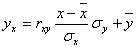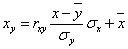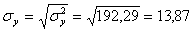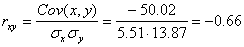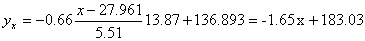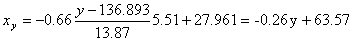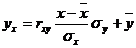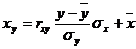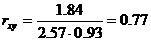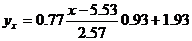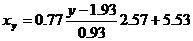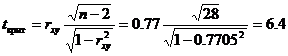Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
а уравнение регрессии с x на y, использовав формулу:
где x x , y — выборочные средние величин x и y, σx, σy — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
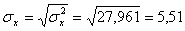
Определим коэффициент корреляции:
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
и уравнение x(y):
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | 0 | 0 |
| 2 | 0 | 6 | 3 | 3 | 0 |
| 3 | 0 | 0 | 1 | 2 | 3 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 0 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 0 | 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 25 | 108 | 44 | 8 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | 0 | 0 | 0 | 0 |
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | 0 | 0 |
| 4 | 0 | 5 | 5 | 13 | 13 | 7 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Скачать
Видео:Математика #1 | Корреляция и регрессияСкачать

Корреляционная таблица
Первоочередной задачей статистической обработки опытных данных является систематизация полученных результатов. Допустим, что в результате исследований для дискретных случайных величин X и У экспериментально определены соответствующие пары значений (х,,)>,). Тогда результаты первичных наблюдений случайных величин X и У с объемом выборки п [равно числу пар (х„у/)] удобно записать в виде табл. 8.1.
Таблица 8.1. Результаты наблюдений случайных величин^ и У
Пусть в результате экспериментов величина X в выборке принимает значения xi, хг, хз,. , х*, а величина У — у, у2, уз, ,yi, где ки I- количество различающихся между собой значений X и У соответственно, причем в общем случае каждые из них в выборке могут повторяться.
Если число наблюдений над случайными величинами X и У велико, то их удобно предварительно сгруппировать и представить в виде табл. 8.2, которую называют корреляционной. Корреляционную таблицу можно рассматривать как статистическое распределение выборки при исследовании двумерного признака объектов генеральной совокупности. В первой строке и столбце таблицы в порядке возрастания перечисляются все встречающиеся в выборке значения величин X и Yсоответственно. На пересечении соответствующих строк и столбцов указываются частоты mlf (i = 1,2,3. #; j = 1,2,3. /), равные количеству появлений пары в выборке. Для иллюстрации частота т2 представляет собой количество появлений в выборке пары (х1уу2). Пустые клетки означают, что соответствующие им частоты равны нулю.
В последней строке таблицы указываются числа тх , равные количеству появлений в выборке значений xh а в последнем столбце -числа mv значенийyj.
Очевидно, что объем выборки
» аблица 8.2. Корреляционная таблица
На основании табл. 8.2 для каждого значения д:„ где / = 1,2,3. можно записать индивидуальный закон эмпирического распределения случайной величины Y (табл. 8.3).
Таблица 8.3. Эмпирическое распределение случайной величины Y
Используя данные этой таблицы, можно определить условное среднее значение ух случайной величины Y, соответствующее значению Х=х,:
Зависимость условного среднего значения ух случайной величины У от величины X, т.е. эмпирическую корреляционную зависимость Уд, удобно представлять в форме табл. 8.4. В первой строке этой таблицы перечислены все встречающиеся в выборке значения величины X, а во второй — вычисленные на основании формулы (8.4) условные средние значения ух величины У.
Таблица 8.4. Эмпирическая корреляционная зависимость
Если при большом объеме выборки содержится немалое число различных значений х, и у, то имеет смысл представить результаты наблюдений случайных величин X и У в виде интервальной корреляционной таблицы (табл. 8.5).
Таблица 8.5. Интервальная корреляционная таблица
Здесь тч — количество появления пары (ад) в выборке, для которых значение х попадает в интервал [x;-i,x/], значение у — в интервал [y,-i,y)]. Количество интервалов, их длина, а также граничные значения хо.уо и хад определяются так же, как и для статистического интервального ряда распределения случайных величин.
Для дальнейших вычислений информацию, представленную в виде интервальной корреляционной табл.8.5, можно преобразовать в обычную корреляционную табл. 8.6, взяв в качестве значений признаков X и Y середины интервалов.
Таблица 8.6. Корреляционная таблица
Здесь х’ = (х, + х,_,) / 2, у. = (у, + у )/2 — центры соответствующих интервалов. В дальнейшем для единообразия корреляционной таблицы удобно от х’,у* перейти к новым переменным
Для наглядности данные корреляционной таблицы изображают в виде так называемого корреляционного поля. Корреляционное поле — это нанесенное в прямоугольной системе координат (рис. 8.1) множество всех п экспериментальных точек с координатами (xij/i). На корреляционном поле строят ломанную линию, соединяющую точки с координатами (х,,ух). Эта линия
называется выборочной ломаной линией регрессии Y на X
(рис. 8.1, г). Если эта линия — прямая (рис. 8.1, а и в), то корреляционная связь между признаками X и Y называется линейной, а если нет (рис.8.1, б) — нелинейной. Если с увеличением X значение ух возрастает, то корреляционная связь называется
прямой (рис. 8.1, а), а если уменьшается — обратной (рис. 8.1, в).
Может случиться, что в данной точке содержится не одна (рис. 8.1, г), а несколько пар точек с координатами (х,у,), извлеченным из корреляционной таблицы. В этом случае эти точки следует немного отделить друг от друга так, чтобы они образовали компактную группу из т,, пар, окружающих данную точку (х,у<). Точки вокруг линии регрессии символизируют разброс возможных значений у, величины У вокруг линии регрессии. Линия регрессии У на X демонстрирует, как в среднем меняется случайная величина У при изменении случайной величины X. По характеру поведения выборочной линии регрессии можно визуально оценить наличие корреляционной эмпирической зависимости по всем статистическим совокупностям X и У.
Рис. 8.1. Корреляционное поле
Пример 8.1. Изучалась зависимость между массой новорожденных павиан-гамадрилов X (в кг) и массой их матерей У (в кг). Результаты наблюдений приведены в табл. 8.7 в виде двумерной выборки.
Таблица 8.7, Массы новорожденных павиан и их матерей
Видео:Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

Как построить корреляционную таблицу
Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
а уравнение регрессии с x на y, использовав формулу:
где x x , y – выборочные средние величин x и y, σx, σy – выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 – 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 – 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения: 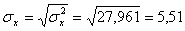
Определим коэффициент корреляции:
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 – 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
и уравнение x(y):
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | ||
| 2 | 6 | 3 | 3 | ||
| 3 | 1 | 2 | 3 | ||
| 5 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 – 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 – 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 – 5.53 • 1.93 = 1.84
Определим коэффициент корреляции: 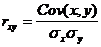
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 – количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X – величина месячной прибыли в тыс. руб., Y – месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y – усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 3 | 6 | ||||||||
| 1 | 25 | 108 | 44 | 8 | 2 | ||||
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | |||
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | |
| 4 | 5 | 5 | 13 | 13 | 7 | 2 | |||
| 5 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | ||
| 6 | 1 | 1 | 2 | 1 | 1 | ||||
| 7 | 1 | 1 | 1 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Видео:Корреляционная таблицаСкачать
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Видео:Функция распределения дискретной случайной величиныСкачать

Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
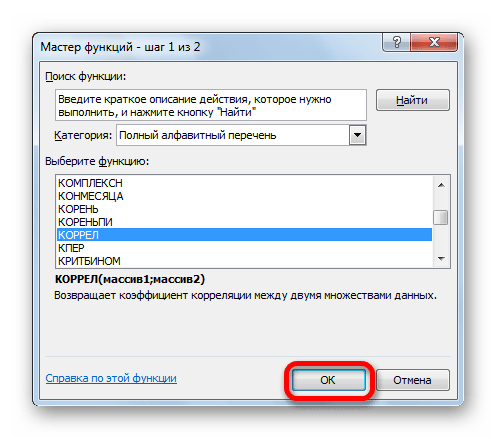
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
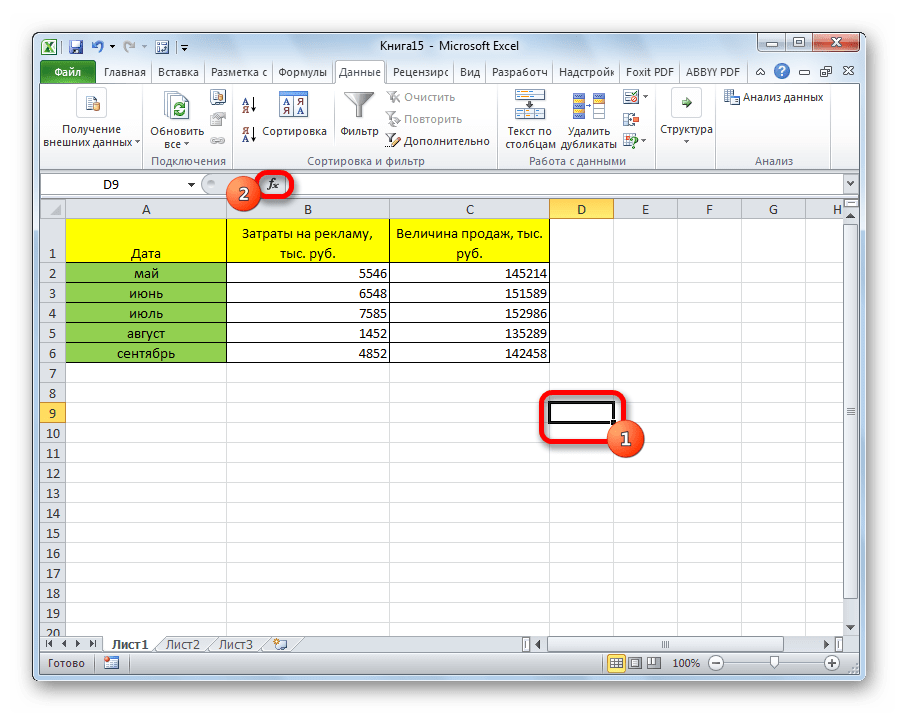
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
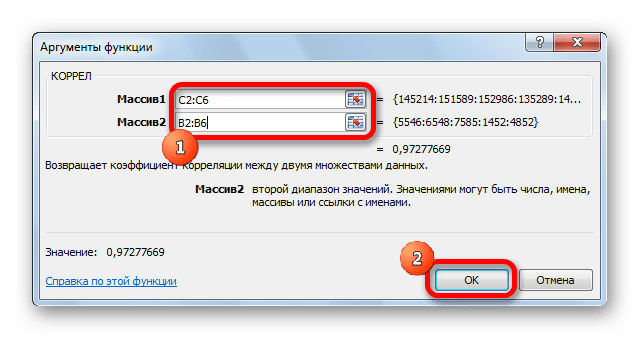
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
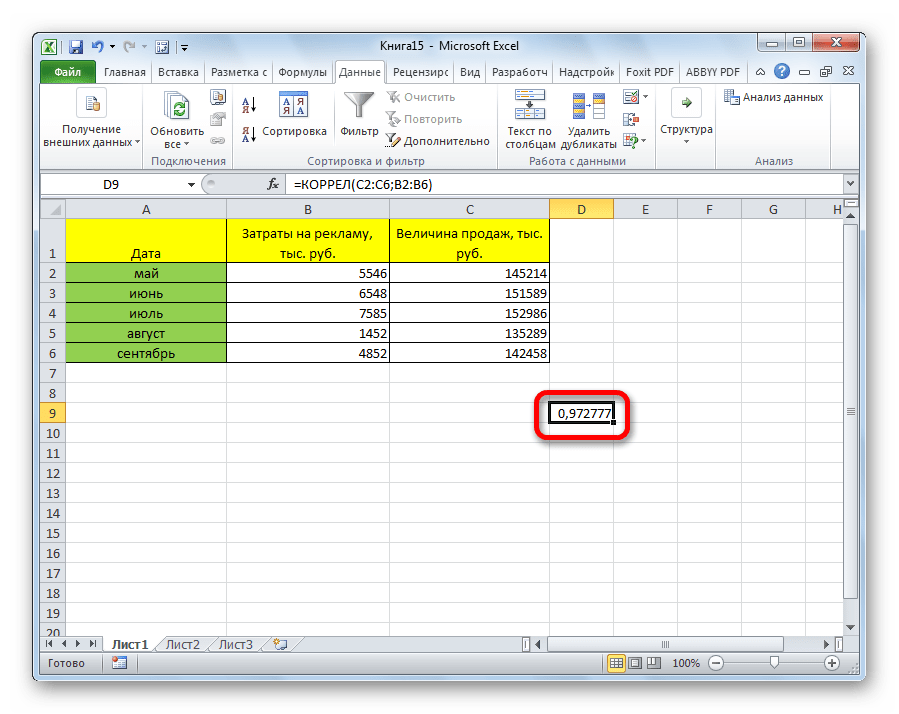
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
В открывшемся окне перемещаемся в раздел «Параметры».
Далее переходим в пункт «Надстройки».
В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
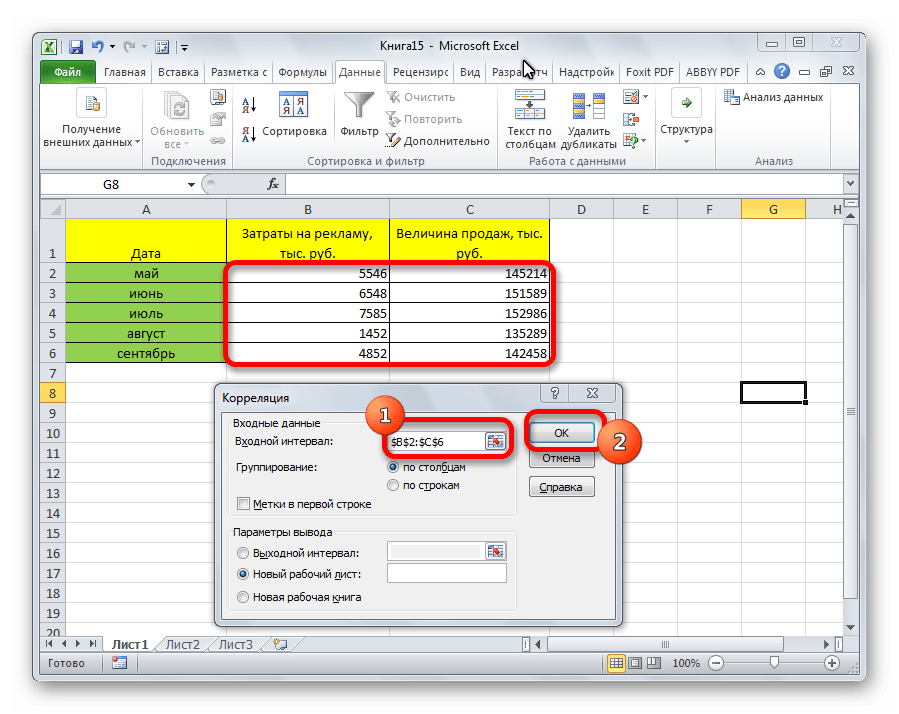
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
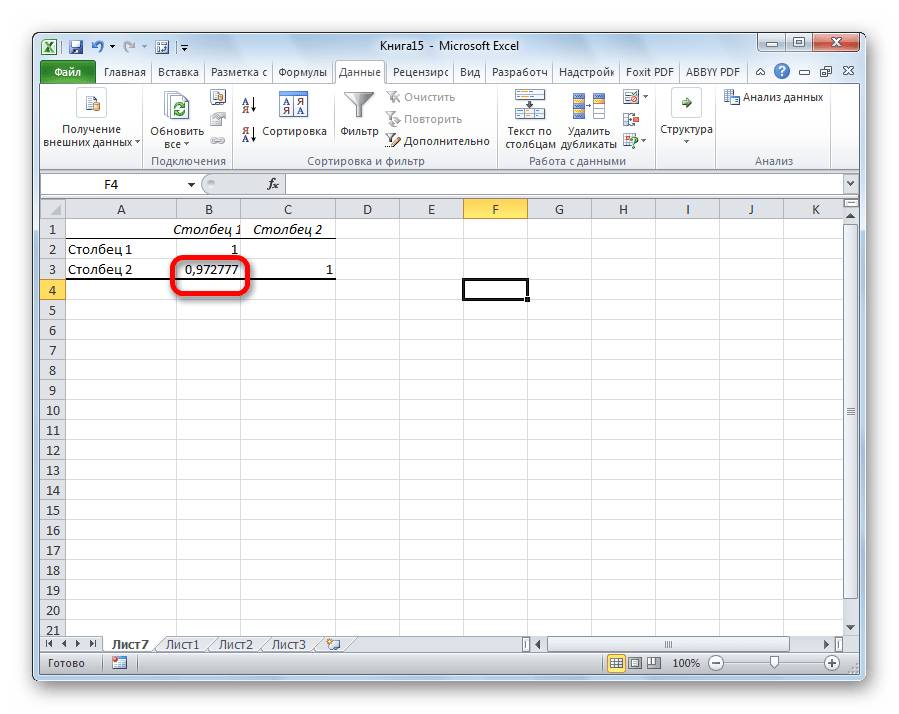
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Корреляционная таблица позволяет изложить материал сжато, компактно и наглядно.
Построение корреляционной таблицы начинают с группировки значений фактического и результативного признаков. Для этого надо разбить все данные значения на требуемое количество интервалов (если количество интервалов не оговаривается в задании, можно выбрать k = 7, 8 или 10). Длина интервала вычисляется по формулам 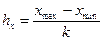
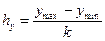
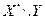 | [ymin, ymin + hy) | [ymin + hy, ymin + 2hy) | … | [ymax – hy, ymax ] | n(y) | 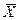 |
| [xmin, xmin + hx) | n11 | n12 | … | n1k | 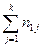 | 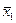 |
| [xmin + hx, xmin + 2hx) | n21 | n22 | … | n2k | 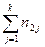 | 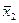 |
| … | … | … | … | … | … | … |
| [xmax – hx, xmax ] | nk1 | nk2 | … | nkk |  | 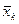 |
| n(x) | 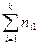 | 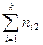 | … | 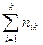 | n | |
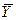 | 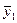 | 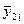 | … | 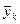 |
Таблица 1. Корреляционная таблица.
Числа nij, полученные на пересечении строк и столбцов, означают частоту повторения данного сочетания значений X и Y, 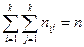
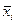
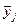
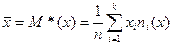
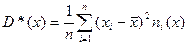
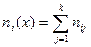
Дата добавления: 2015-09-11 ; просмотров: 3232 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📺 Видео
Корреляция и ковариация двумерной случайной величиныСкачать

Случайный вектор двумерной случайной величиныСкачать

Коэффициент корреляции Пирсона в ExcelСкачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Лекция №12 по теории вероятностей. Нормальные случайные векторы. Широков М.Е.Скачать

Расчет коэффициента корреляции в ExcelСкачать

Лекция 7. Корреляционный анализСкачать

Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать

Стрим с Борисом Надеждиным, Екатериной Дунцовой и Дмитрием КисиевымСкачать

Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Коэффициент корреляции. ТемаСкачать

Случайные процессы Лекция 1Скачать

Коэффициент корреляции. Дискретное распределениеСкачать

Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать

О корреляционной функции и её аналитическом вычисленииСкачать