Вписанная и описанная окружность 8 класс конспект урока атанасян (7 видео)

Конспект урока по геометрии на тему «ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Содержание

УРОКИ-КОНСПЕКТЫ ПО ГЕОМЕТРИИ 8 КЛАСС
Вписанная и описанная окружность
Просмотр содержимого документа «вписанная и описанная окружность»
Конспект урока по геометрии в 8 классе «Вписанная окружность»
Просмотр содержимого документа «Конспект урока по геометрии в 8 классе «Вписанная окружность»»
🎬 Видео

Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

УРОКИ-КОНСПЕКТЫ ПО ГЕОМЕТРИИ 8 КЛАСС

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ

Цели: ввести понятие вписанной окружности и описанного около окружности многоугольника; рассмотреть теорему о том, что в любой треугольник можно вписать окружность.

I. Проверка домашнего задания.

1) а) Докажите, что АВМ = МСА.

б) АМ = 4, МD = 3, ВD = 4.

Найдите расстояние от точки М до стороны АС.

2) Найдите МKN и расстояние MN, если ОМ = , KМ = 3.

3) Найдите углы АВС, если ОАС = 20° и АОС = 120°.

4) стороны угла А касаются окружности радиуса r с центром О.

а) Найдите ОА, если r = 5 см, А = 60°.

б) Найдите r, если ОА = 14 дм, А = 90°.

II. Изучение нового материала.

Изложить в виде лекции п. 74 до замечания 2.

III. Закрепление изученного материала.

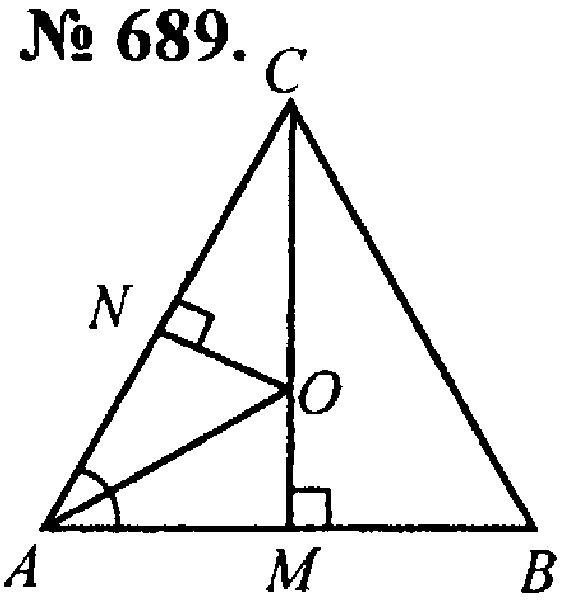
Выполнить №№ 701 (для остроугольного треугольника), 689, 691.

1) Центр О вписанной окружности искомого радиуса r лежит на биссектрисе СМ треугольника АВС, а так как СМ АВ, то вписанная окружность касается отрезка АВ в точке М. Поэтому ОМ = r.

Далее обсудить с учащимися различные способы решения этой задачи:

1. АМ = AB = 5 см.

2. M и N – точки касания, следовательно, AN = АМ = 5 см, откуда CN = АС – АN = 8 cм.

3. В АСМ : СМ = = 12 (см).

4. В СON : СО2 = СN2 + ON2, то есть (12 – r )2 = 82 + r 2

144 – 24r + r2 = 64 + r2.

r = 3 .

ОМ = ON = 3 см .

1. В АСМ : АМ = AB = 5 см.

СМ = = 12 (см).

2. Отрезок АО – биссектриса треугольника АМС (так как О – центр вписанной окружности), поэтому или ; 13r = 60 – 5r, r = 3.

ОМ = ОN = 3 см.

1) Центр вписанной в треугольник окружности в точке пересечения биссектрис;

2) ОМ = ON = ОK – радиусы вписанной окружности;

3) окружность единственная для данного треугольника.

Домашнее задание: вопросы 21, 22, с. 188; №№ 701 (для прямоугольного и тупоугольного треугольников), 637, 690, 693 (а), 693 (б) – по желанию и используя № 697 III способ решения № 698.

1) О – центр вписанной окружности в треугольник АВС, который лежит на высоте (биссектрисе) равнобедренного треугольника, проведенной к основанию.

2) ОМ = ОD – радиусы этой окружности.

3) Пусть k – коэффициент пропорциональности, тогда ОВ = 12k см, ОD = ОМ = 5k см.

4) Прямоугольные треугольники ВDС и ВМО имеют общий угол В, и, значит, ВDС ВМО по первому признаку.

5) .

6) Из прямоугольного треугольника ВDС по теореме Пифагора имеем:DС = .

7) ; 5 = ;

625 = 3600 – 289k2

k2 = .

8) DC = = 25 (cм).

1) АС || ОN, так как АС СВ и ON CВ.

СВ || ОK, так как СВ АС и OK АС, значит, четырехугольник KONC – прямоугольник, а так как KО = CN = r = ON = KC, то KONC – квадрат.

2) АKО = АМО (по катету и гипотенузе), поэтому АK = АМ.

3) ВNO = ВМО (по катету и гипотенузе).

4) РАВС = АВ + ВС + АС = АМ + МВ + NB + CN + KC + АK.

РАВС = 2АМ + 2MВ + 2CN = 2(АМ + МВ + СN).

а) РАВС = 2(АВ + СN) = 2(26 + 4) = 60 (см).

б) Из АВС, С = 90° имеем по теореме Пифагора:

АС2 = АВ2 – СВ2 = АВ2 – (CN + NB) = 172 – (5 + r)2

ВС2 = АВ2 – АС2 = АВ2 – (АK + KС) = 172 – (12 + r)2

172 = 172 – (5 + r)2 + 172 – (12 + r)2

2r2 + 34r – 120 = 0

r = 3 (второй корень не удовлетворяет условию задачи).

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная и описанная окружность

представляет собой конспект урока по теме «Вписанная и описанная окружность» для учащихся 8 класса (геометрия, учебник Атанасян Л. С.). Цель: обобщить и систематизировать знания по теме «Вписанная и описанная окружность»; уметь применять их в стандартных ситуациях и при решении задач.

Просмотр содержимого документа
«вписанная и описанная окружность»

ПЛАН-КОНСПЕКТ УРОКА
по геометрии по теме «Вписанная и описанная окружность»

Тема – «Вписанная и описанная окружность»(4 урок в теме)

Базовый учебник «Геометрия», 7-9 классы, Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

Цель и задачи урока

Цель: обобщить и систематизировать знания по теме «Вписанная и описанная окружность»; уметь применять их в стандартных ситуациях и при решении задач;

обобщить и систематизировать знания по теме «Вписанная и описанная окружность»; уметь применять их в стандартных ситуациях и при решении задач;

научиться выдвигать гипотезы, уметь преобразовывать теоретический материал в способы деятельности, обобщать изученный материал;

-формирование эмоционально-целостного отношения к предмету; превращение предметного знания в личностное знание;

урок обобщения и систематизации знаний

Формы работы учащихся: групповая, фронтальная, дифференцированная.

Необходимое техническое оборудование: доска и мел; компьютер, экран и проектор;10 компьютеров с выходом в Интернет (по 2 ученика за компьютером)

СТРУКТУРА И ХОД УРОКА

Название используемых ЭОР

(с указанием порядкового номера из Таблицы 2)

(с указанием действий с ЭОР, например, демонстрация)

Проверка готовности к уроку

Готовятся к уроку, проверяют наличие чертежных инструментов

На дом вам было дано задание: поработать с интерактивными задачами и упражнениями. Давайте проверим выполнение этих заданий. Работаем в парах.

Учащиеся работают с интерактивными приложениями, демонстрируя друг другу выполнение заданий.

Мы изучили тему »Вписанная и описанная окружность». Повторим основные теоретические вопросы. На доске предложен ряд задач. (Слайд 1-3)

«Предложи свой вариант решения задачи», найдите рациональный вариант решения.

Задачи на готовых чертежах

Параллельно задаются вопросы:

Можно ли в параллелограмм вписать окружность?

А описать около него окружность?

Чтобы хорошо решать задачи, нужно ориентироваться в теории. Давайте повторим основные разделы изучаемой темы.

(Предлагается решить небольшой тест)(Слайд4)

Работа в режиме презентации-

фронтальный устный опрос

Учащиеся выполняют устно задание.

( Не всегда, надо чтобы суммы противоположных сторон были равны)

( Нет, не всегда, сумма противоположных углов должна быть 180 0 )

Учащиеся выполняют тест на листочках с последующей устной фронтальной проверкой.

Мы повторили и еще раз озвучили основные факты по теме. Предлагаю вам в тетради решить задачу, лежащую на столе, для каждой группы.(слайд 5)

Задание: каждый из вас в тетради решает предложенную задачу,

затем в своей группе вы обсуждаете, сверяете своё решение, к доске выходит 1 человек и дает алгоритм решения задачи.

Вы имеете право задать вопрос о ходе решения задачи и должны услышать правильный ответ на него.

Задача: Угол, противолежащий основанию равнобедренного треугольника, равен 120 0 , боковая сторона 8 см. Найти: диаметр описанной окружности.

Задача: Два угла треугольника равны 80 0 и 70 0 . Под каким углом видна каждая его сторона из центра вписанной окружности?

(105 0 , 130 0 , 125 0 )

Задача: Три стороны описанного четырехугольника относятся (в последовательном порядке) как 1:2:3. Найти: его стороны, если Р=24см.

1) Четырехугольник ABCD вписан в окружность, сторона AD — диаметр окружности, 0 , 0 . Найти: 0 , 50 0 , 90 0 )

2) Можно ли описать окружность около четырехугольника, углы которого относятся как 2:4:5:3?

Учащиеся разбиваются на группы по 4 человека и решают предложенные задачи.

Помогают друг другу.

Решение и обсуждение

Внимание! Время истекло. К доске: представитель I группы, II группы, III группы и IVгруппы.

Учитель руководит работой ученика у доски, корректирует его деятельность, задает вопросы по теории, исправляет ошибки, выставляет оценки.

Рассказывают решение задачи, отвечают на вопросы остальных учащихся.

— Дайте характеристику вашей сегодняшней деятельности в соответствии с темой урока.

– В каких новых ситуациях вы использовали свои знания?

— Какой ценный опыт приобрели?

— Проанализируйте свою работу в группах, обратите внимание, что более успешно выполнила задания группа, которая правильно организовала свой труд. Учтите это в будущем.

В качестве домашнего задания предлагается интерактивный тест (приложение3)

— Сегодня на уроке мы повторили свойства вписанной и описанной окружности, решали задачи на применение этих свойств. Эти умения помогут нам при выборе более рационального пути в решении задач.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Конспект урока по геометрии в 8 классе «Вписанная окружность»

Конспект урока по геометрии в 8 классе «Вписанная окружность».

Интеркативный тест на закрепление знаний.

Просмотр содержимого документа
«Конспект урока по геометрии в 8 классе «Вписанная окружность»»

Урок по геометрии в 8 классе

Тема урока: «Вписанная окружность»

Цели урока: доказательство теоремы об окружности, вписанной в треугольник.

Образовательные: создать условия для введения понятий вписанной и описанной окружностей, сформулировать и доказать теорему об окружности, вписанной в треугольник. Рассмотреть задачи на применение доказанного утверждения. Выполнить тест на проверку.

Развивающие: развитие умений учебно-познавательной деятельности, умение анализировать, обобщать полученные знания, развитие гибкости мыслительных процессов, развивать математическую речь.

Воспитательные: воспитание инициативности, самостоятельности, способности к творческой деятельности, воспитание культуры математического мышления.

Тип урока: комбинированный урок.

Формы организации урока: индивидуальная, фронтальная, работа в парах.

Метод обучения: лекция, практические задания.

Учебник: Геометрия7-9, Л.С. Атанасян, В.Ф.Бутузов М.: «Просвещение».

1.Организационные моменты. Озвучивание темы урока.

2. Актуализация знаний учащихся.

3. Изучение нового материала.

4. Закрепление изученного материала.

5. Домашнее задание.

1. Организационные моменты. Озвучивание темы урока.

Здравствуйте, ребята! Сегодня на уроке мы познакомимся с понятием вписанная окружность.

2. Актуализация знаний учащихся.

Повторить теоретический материал: окружность, касательная, вписанные и описанные фигуры, биссектриса, равноудаленная точка, перпендикуляр.

Предложить решить задачи по готовым чертежам (дать учащимся 2-3 минуты на обдумывание, а далее обсудить возможные варианты решений)

Задача 1

Задача 2

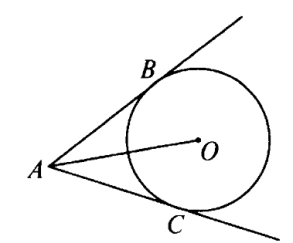
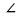
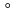
Дано: АВ, АС – касательные, В, С – точки касания. ВАС = 56 , ОС = 4 см.

Найти: 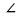АОВ, ОВ.

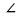
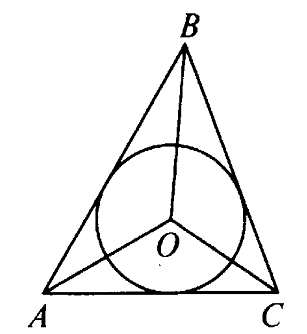
Решение: АОВ = 28 (доказываем равенство треугольников АОВ и АОС); ОС=ОВ= 4 см.

Дано: АВ, ВС, АС – касательные, ВОС = 120 , АВО = 25 , АОС = 115 .

Найти: углы треугольника АОВ.

Доказать: О – точка пересечения биссектрис треугольника АОВ.

Решение: ВОА=360-120-115=125 ; ОАВ=180-25-125=30 .

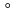
3. Изучение нового материала.

Вводим понятие окружности, вписанной в многоугольник.

На доске демонстрация чертежей (презентация, чертеж мелом, интерактивная доска).

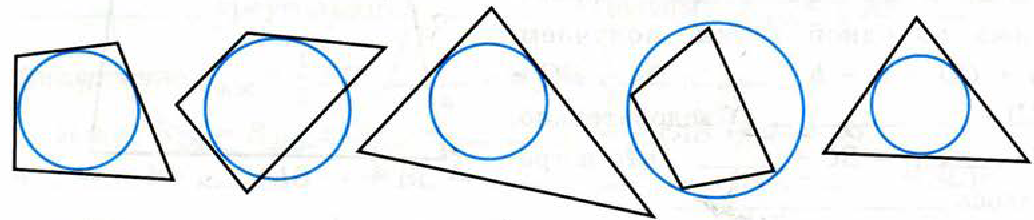
Определение: Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

Вопрос: в Задаче 2 (см. выше) какой будет являться окружность? (Вписанной)

Рассмотреть примеры на доске, ответить на вопросы (Можно ли вписать окружность в многоугольник? (да) Как располагается окружность относительно сторон многоугольника? (стороны многоугольника являются касательными к окружности)).

Т еорема: В любой треугольник можно вписать окружность.

Ответим вместе на вопрос: Как построить вписанную окружность в заданный треугольник? Для этого докажем теорему.

Рассмотрим произвольный треугольника АВС. Проведем биссектрисы углов ∆. Они пересекутся в точке О. Проведем из точки О перпендикуляры ОК, ОL и ОМ. Т.к. точка О равноудалена от сторон треугольника АВС, то ОК=ОМ=ОL.

Скажите, что из этого следует?

(ОК, ОМ и ОL являются радиусами окружности; треугольники АКО и АМО — прямоугольные, АО- общая сторона, углы КАО и МАО равны т.к. АО биссектриса)

Видим, что треугольники КАО и МАО равны, почему? Верно, окружность проходит через точки К, L, М, а стороны треугольника касаются окружности в этих точках (т.к. они перпендикулярны к радиусам ОК, ОL, ОМ). Значит окружность с центром в точке О является вписанной в треугольник АВС. Теорема доказана.

Открываем учебник стр. 179-180 и записываем Замечание 1 и Замечание 2.

В треугольник можно вписать только одну окружность.

Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности.

4. Закрепление изученного материала.

Разберем задачу по готовому чертежу (условие задачи и чертеж: раздаточный материал):

Ответ: 28 см. (Взаимопроверка в парах).

Решаем задачи из учебника №691, №689:

№ 689: у доски работает один ученик, остальные в тетрадях.

Указание к задаче: в данной задаче радиус вписанной окружности лучше находить, используя формулу S=1/2 Pr. Сначала найдите площадь треугольника по формуле S=1/2 ha или по формуле Герона (стр. 130), найдите периметр треугольника и вычислите радиус r=S/(1/2 P) или r=2S/P.

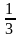
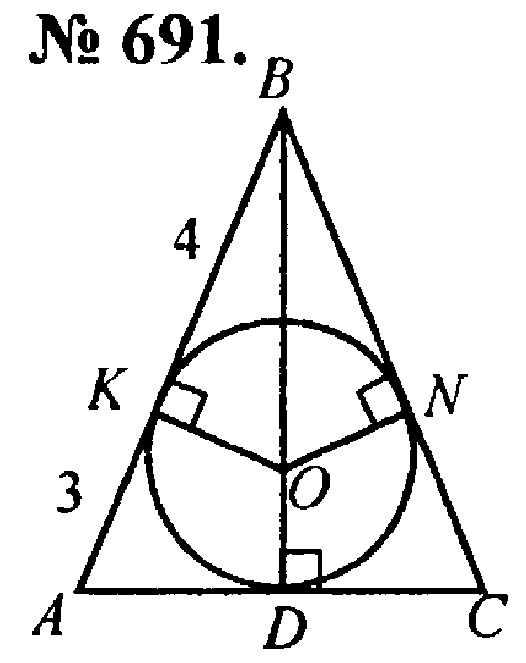
Ответ: r=3 см.

№ 691: ученики решают самостоятельно (учитель контролирует работу учащихся, которым требуется помощь и консультирует остальных):

Решение: Т.к. АВ, ВС, АС- касательные, К, N, D- точки касания, то АК=АD, СD=CN, BK=BN.

Т.к. АВ=ВС, то СN=CD=3см, следовательно

Итог урока: После решения задач учитель задает классу вопросы (участвует весь класс).

Мы отлично поработали.

Подведем итоги, что нового мы узнали на уроке?

(что такое вписанная окружность, доказали теорему, свойства вписанной окружности)

Чему научились на уроке? (применять новые знания к решению задач)

5. Домашнее задание: № 690, № 693, вопросы к главе 21, 22; пройти интерактивный тест по ссылке https://docs.google.com/forms/d/1wTVnIYol2WKMi_LWDsekMSJxJu44N5v0Ha1d8g3_Fkc/edit

Вопросы в тесте:

Периметр треугольника равен 36, а радиус вписанной окружности равен 7. Найдите площадь этого треугольника. (Ответ: 126)

Площадь треугольника равна 132, а радиус вписанной окружности равен 6. Найдите периметр этого треугольника. (Ответ: 44)

Боковые стороны равнобедренного треугольника равны 13, основание равно 24. Найдите радиус вписанной окружности. (Ответ: 2,4)