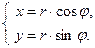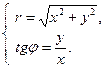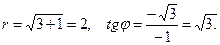Читайте также:
|
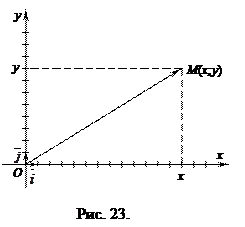 |
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба берут обычно одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения О – началом координат. Одну из осей называют осью абсцисс (осью Оx), другую – осью ординат (осью Оy) (рис. 23).
На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат − вертикально и направленной снизу вверх. Оси координат делят
плоскость на четыре области – четверти (или квадранты).
Единичные векторы осей обозначают 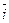
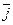
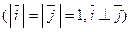
Систему координат обозначают Oxy (или 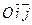
Рассмотрим произвольную точку М плоскости Oxy. Вектор 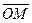
Координатами точки М в системе координат Oxy ( 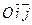
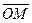
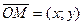
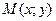
Эти два числа х и у полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка М плоскости, и наоборот.
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Оp,
называемой полярной осью, и единичным вектором 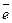
Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием r от полюса О и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24).
Числа r и φ называются полярными координатами точки М, пишут 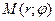
Для построения всех точек плоскости достаточно полярный угол φ ограничить промежутком 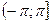
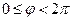
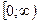
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось с положительной полуосью Ох. Пусть х и у – прямоугольные координаты точки М, а r и φ – ее полярные координаты.
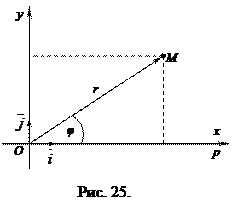 |
Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:
Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами:
Определяя величину φ, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что 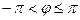
Пример 9.1. Дана точка 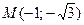


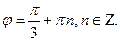
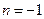
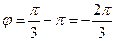
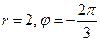
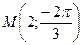
Дата добавления: 2015-01-15 ; просмотров: 11 ; Нарушение авторских прав
Видео:Правые и левые тройки векторовСкачать

3.5.5 Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
Видеоурок: Опыты Герца. Свойства электромагнитных волн
Лекция: Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
Опыты Максвелла доказали, что электрический ток в вакууме распространяется со скоростью, с которой движется свет, то есть 3*10 8 м/с.
При движении зарядов, которые создают ток, образуется две составляющих поля — электрическое и магнитное поле.

Чем быстрее будет происходить перемещение заряда, тем выразительнее будут электромагнитные волны. То есть, чем больше частота, тем большая интенсивность электромагнитных волн.
На частоту колебательного контура влияет индуктивность и ёмкость составляющих элементов цепи. Определить её можно по следующей формуле:
Электромагнитные волны являются поперечными. Это значит, что колебания магнитного и электрического поля происходят в плоскостях, которые являются параллельными к распространению волны.
На графике можно рассмотреть электрическую и магнитную составляющую электромагнитной волны.
Стоит отметить, что силовые характеристики магнитного и электрического поля находятся под углом 90 градусов друг к другу.
На графике показана длина волны, которая обозначается λ. Для её определения необходимо воспользоваться формулой:

Электромагнитным волнам присущи все правила, справедливые для механических волн:
1. Стоит отметить, что электромагнитная волна способна отразиться от плотного металла.
2. Через диэлектрик электромагнитная волна проходит достаточно проблематично, поскольку она им поглощается.
3. Если электромагнитная волна переходит из одной среды в другую, которая отличается плотностью, то она способна преломиться.
Видео:Векторное произведение векторовСкачать

Что такое взаимная ориентация векторов
Для дальнейшего изучения свойств пространства необходимо ввести определение ориентации пространства. Строгая теория, касающаяся этого понятия не очень сложна, но достаточно суха. В связи с этим ограничимся лишь некоторыми “качественными” пояснениями.
Итак, все упорядоченные некомпланарные тройки векторов могут быть разбиты на два непересекающихся класса: правые тройки и левые тройки.
Определение 1: Упорядоченная тройка некомпланарных векторов а 1 , а 2 , а 3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а 1 к а 2 и от а 2 к а 3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.
Есть и ещё один способ разделить эти два класса:
Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая.
Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададим ориентацию пространства.
Далее будем считать положительными правые тройки векторов. Все дальнейшие определения будем давать с учетом этого
Определение 2: Скалярное произведение ставит в соответствие паре векторов a и b число ( a , b )=| a | · | b | · cosφ a , b .
Свойства скалярного произведения:
1. коммутативность: ( a , b )=( b , a )
3. ( a , b )=0 a 
4. Дистрибутивность: ( a 1 + а 2 , b )= ( a 1 , b )+ ( a 2 , b )
5. ( а , λ ·b )= λ · ( a , b ) 

Утверждение 1: В декартовом базисе если а =, b =, то ( a , b )= x 1 · x 2 + y 1 · y 2 + z 1 · z 2 .
Пример 1. Найти угол между векторами.
Определение 3: Векторным произведением упорядоченной пары векторов a и b называется вектор [ a , b ], такой что
- | [ a , b ] |=S a , b , где S a , b – площадь параллелограмма, построенного на векторах a и b . (Если a || b , то S a , b =0.)
- a
[ a , b ]
b .
- a, b , [ a , b ] – правая тройка.
Свойства векторного произведения:
- [ a , b ] = -[ b , a ]
- [ a , b ] = θ ó a || b
- [ a 1 + a 2 , b ] = [ a 1 , b ]+[ a 2 , b ]
- λ·[ a , b ] = [λ ·a , b ] = [ a ,λ ·b ]
λ
R .
Утверждение 2: В декартовой системе координат (базис i , j , k ), a =, b =
=> [ a , b ] =
=
Пример 2. Вычислить площадь параллелограмма, построенного на векторах a и b.
Определение 4: Смешанным произведением упорядоченной тройки векторов a , b и c называется число , b , c> , т.ч. a , b , c >=([ a , b ], c ).
Утверждение 3: a , b , c >=V a , b , c , если a , b , c – правая тройка, или a , b , c >= -V a , b , c , если a , b , c – левая тройка. Здесь V a , b , c – объём параллелепипеда, построенного на векторах a , b и c . (Если a , b и c компланарны, то V a , b , c =0.)
Утверждение 4: В декартовой системе координат, если a =, b =,
с =, => a , b , c >=
Пример 3. Проверка компланарности векторов.
Пример 4. Принадлежность 4 точек одной плоскости.
Пример 5. Вычислить объем тетраэдра и его высоту.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
📹 Видео
§11 Ориентация векторов в пространствеСкачать

Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Смешанное произведение векторовСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Аналитическая геометрия, 3 урок, Векторное произведениеСкачать

Разложение вектора по базису. 9 класс.Скачать

Линейная зависимость векторов на примерахСкачать

Тема: Движения. Урок: Что такое векторыСкачать

§18 Свойства смешанного произведенияСкачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Как разложить вектор по базису - bezbotvyСкачать

Свойства электромагнитных волн | Физика 11 класс #21 | ИнфоурокСкачать

 ,
,  и
и 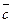 основано на следующих соображениях. Если
основано на следующих соображениях. Если 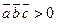 , то
, то 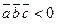 , то
, то 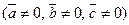 :
: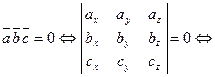 векторы
векторы 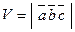 , а объем треугольной пирамиды, построенной на этих же векторах, равен
, а объем треугольной пирамиды, построенной на этих же векторах, равен 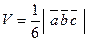 .
.
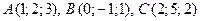 и
и 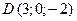 . Найти объем пирамиды.
. Найти объем пирамиды. Решение. Находим векторы
Решение. Находим векторы 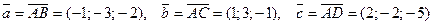 .
.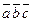 :
: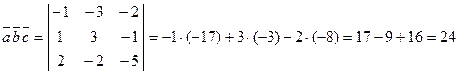 .
. Следовательно,
Следовательно, 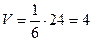 .
.