Основание равнобедренного треугольника через высоту

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Онлайн калькулятор

Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

• длину двух равных сторон (a) и длину основания (b)
• длину двух равных сторон (a) и угол α
• длину двух равных сторон (a) и угол β
• длину основания (b) и угол α
• длину основания (b) и угол β

Введите их в соответствующие поля и получите результат.

Если известны длина стороны а и основания b

Чему равна высота h равнобедренного треугольника если длина сторон , а длина основания

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?

Формула

h = √ a 2 — ( b /₂) 2

Пример

Если сторона a = 10 см, а сторона b = 5 см, то:

h = √ 10 2 — ( 5 /₂) 2 = √ 100 — 6.25 ≈ 9.68 см

Если известны длина стороны а и угол α

Чему равна высота h равнобедренного треугольника если длина сторон , а угол

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?

Формула

Пример

Если сторона a = 5 см, а ∠α = 45°, то:

h = 5⋅sin 45 ≈ 3,53 см

Если известны длина стороны а и угол β

Чему равна высота h равнобедренного треугольника если длина сторон , а угол

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?

Формула

Пример

Если сторона a = 5 см, а ∠β = 30°, то:

Если известны длина стороны b и угол α

Чему равна высота h равнобедренного треугольника если длина основания , а угол

Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?

Формула

Пример

Если сторона b = 20 см, а ∠α = 35°, то:

Если известны длина стороны b и угол β

Чему равна высота h равнобедренного треугольника если длина основания , а угол

Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол β?

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Видео:№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Видео:№261. Докажите, что в равнобедренном треугольнике высоты, проведенные из вершин основания, равны.Скачать

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

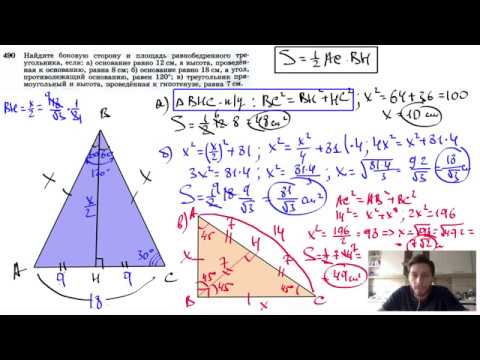
Видео:№490. Найдите боковую сторону и площадь равнобедренного треугольника, если: а) основание равноСкачать

Высота и сторона «A» равнобедренного треугольника

Видео:№255. В равнобедренном треугольнике CDE с основанием СЕ проведена высота CF.Скачать

Свойства

Так как высота равнобедренного треугольника, опущенная на основание, является одновременно и биссектрисой и медианой, следовательно, она делит основание и угол при вершине на две равные части, образуя прямоугольный треугольник со сторонами a и b/2. Из теоремы Пифагора в таком треугольнике можно найти само основание, а затем рассчитать все остальные возможные данные. (рис.88.2) h^2+(b/2)^2=a^2 b=√(a^2-h^2 )/2

Чтобы вычислить периметр равнобедренного треугольника, надо к двум боковым сторонам прибавить основание или приведенный выше радикал через высоту. P=2a+b=2a+√(a^2-h^2 )/2

Площадь равнобедренного треугольника через высоту и основание по определению вычисляется как половина их произведения. Заменив основание на соответствующее ему выражение, получаем площадь через высоту и боковую сторону равнобедренного треугольника. S=hb/2=(h√(a^2-h^2 ))/4

В равнобедренном треугольнике равны не только боковые стороны, но и углы при основании, а так как в сумме они дают всегда 180 градусов, то любой из углов можно найти, зная другой. Первый угол вычисляется по теореме косинусов, приведенной для равных боковых сторон, а второй можно найти через разность от 180. (рис.88.1) cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 ) α=(180°-β)/2 β=180°-2α

Центральные медиана и биссектриса, опущенные на основание совпадают с высотой, а боковые медианы, высоты и биссектрисы можно найти по следующим формулам для равнобедренных треугольников. Чтобы вычислить их через высоту и боковую сторону, нужно заменить основание на эквивалентное ему выражение. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

Высота, опущенная на боковую сторону, через высоту, опущенную на основание и боковую сторону равнобедренного треугольника. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a=(√(a^2-h^2 ) √((4a^2-a^2+h^2)))/2a=√((a^2-h^2)(3a^2+h^2))/2

Биссектрисы, направленные в боковые стороны, также могут быть выражены через боковую сторону и центральную высоту треугольника . (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=√(a(a^2-h^2)(2a+√(a^2-h^2 )) )/(a+√(a^2-h^2 ))

Средняя линия проводится параллельно любой стороне треугольника, соединяя середины боковых в ее отношении сторон. Таким образом, она всегда оказывается равна половине параллельной ей стороны. Вместо неизвестного основания в формулу можно подставить используемый радикал, чтобы найти среднюю линию через высоту и боковую сторону равнобедренного треугольника(рис. 88.5) M_b=b/2=√(a^2-h^2 )/2 M_a=a/2

Радиус окружности, вписанной в равнобедренный треугольник, начинается от точки на пересечении биссектрис и уходит перпендикулярно в любую из сторон. Чтобы его найти через высоту и боковую сторону треугольника, надо заменить основание в формуле на радикал. (рис. 88.6) r=1/2 √(((a^2-h^2)(2a-√(a^2-h^2 )))/(2a+√(a^2-h^2 )))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы путем подстановки радикала через высоту и боковую сторону вместо основания. (рис. 88.7) R=a^2/√(3a^2-h^2 )

🎥 Видео

Уравнения стороны треугольника и медианыСкачать

Задача на самую забываему теорему планиметрии | Планиметрия 81 | mathus.ru #егэ2024Скачать

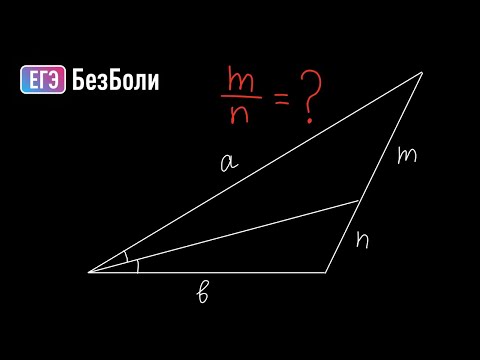
Геометрия Основание равнобедренного треугольника относится к его высоте опущенной на основание какСкачать

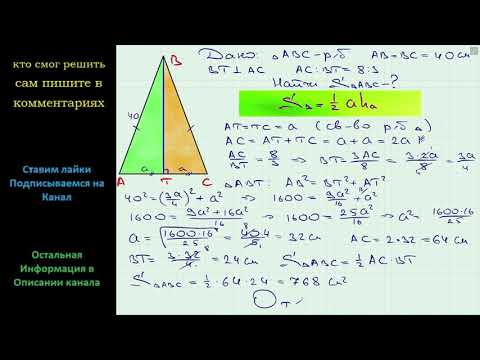
НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

В равнобедренном треуг один из углов 120 , основание 4см, найдите высоту проведенную к бок сторонеСкачать

№487. Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 смСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

№265. В равнобедренном треугольнике ABC с основанием АС проведены биссектриса AF и высота АН.Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

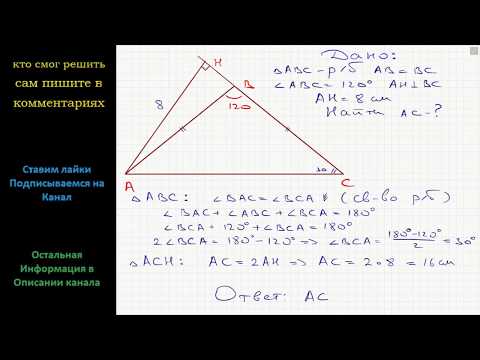
Геометрия Угол, противолежащий основанию равнобедренного треугольника, равен 120, а высотаСкачать