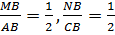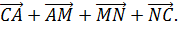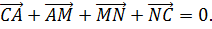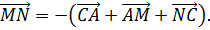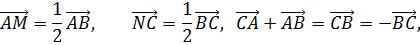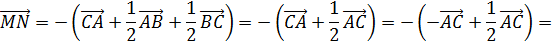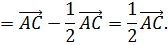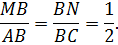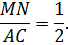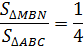Km средняя линия треугольника abc укажите для каждого из векторов в левом столбце (4 видео)

Диагностическая работа по геометрии в 8 классе (Погорелов А.В.)

Контрольные измерительные материалы позволяют осуществить оценку предметных и метапредметных компетенций, в том числе овладение межпредметными понятиями и способность использования УУД в учебной и познавательной практике.

Содержание

Содержимое разработки
Средняя линия треугольника — свойства, признаки и формулы
Определение и признаки средней линии треугольника
Теорема о средней линии треугольника
Доказательства
Следствия из теоремы с доказательствами
Следствие №1
Следствие №2
Свойства средней линии треугольника
Средняя линия прямоугольного треугольника
Пример решения задачи
Что такое средняя линия треугольника
Определение средней линии треугольника
Свойства средней линии треугольника
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Признак средней линии треугольника
Пример задачи
🎥 Видео

Содержимое разработки

Описание контрольных измерительных материалов для осуществления оценки качества образования по геометрии обучающихся 8 классов

На основании письма Федеральной службы по надзору в сфере образования и науки (Рособнадзор) №05-71 от 16.03.2018 «О направлении рекомендаций по повышению объективности оценки образовательных результатов».

Контрольные измерительные материалы позволяют осуществить оценку предметных и метапредметных компетенций, в том числе овладение межпредметными понятиями и способность использования универсальных учебных действий (УУД) в учебной и познавательной практике.

Результаты могут быть использованы общеобразовательными организациями, муниципальными и региональными органами исполнительной власти, осуществляющими государственное управление в сфере образования, для анализа текущего состояния муниципальных и региональных систем образования и формирования программ их развития.

2. Документы, определяющие содержание работы

Содержание и структура диагностической работы определяются на основе Федерального государственного образовательного стандарта основного общего образования (приказ Минобрнауки России от 17.12.2010 № 1897) с учётом Примерной основной образовательной программы основного общего образования (одобрена решением федерального учебно-методического объединения по общему образованию (протокол от 08.04.2015 № 1/15).

Задания КИМ ориентированы на учебник А.В. Погорелова «Геометрия 7-9 классы», включённого в Федеральный перечень Минобрнауки РФ на 2018–2019 учебный год.

3. Структура работы

Вариант диагностической работы состоит из 10 заданий, которые различаются по содержанию и проверяемым требованиям.

Задания 1-7 решить и дать ответ.

В заданиях 8-10 требуется самостоятельно записать правильное решение в развернутом виде.

4. Кодификаторы проверяемых элементов содержания и требований к уровню подготовки участников

В табл.1 приведен кодификатор проверяемых элементов содержания

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Средняя линия треугольника — свойства, признаки и формулы

Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.

Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.

Видео:9 кл Геометрия КР№1 ВекторыСкачать

Определение и признаки средней линии треугольника

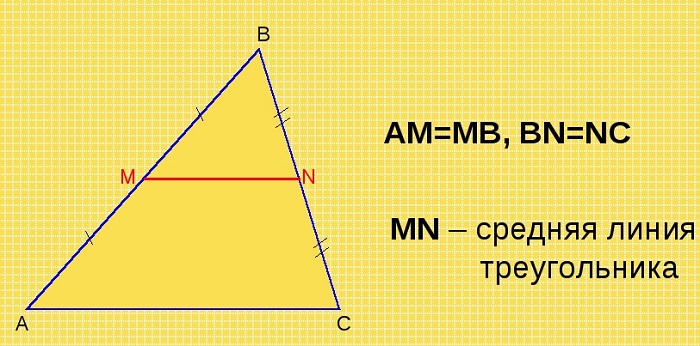
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.

Доказательство следует из теоремы Фалеса.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Теорема о средней линии треугольника

Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.

Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.

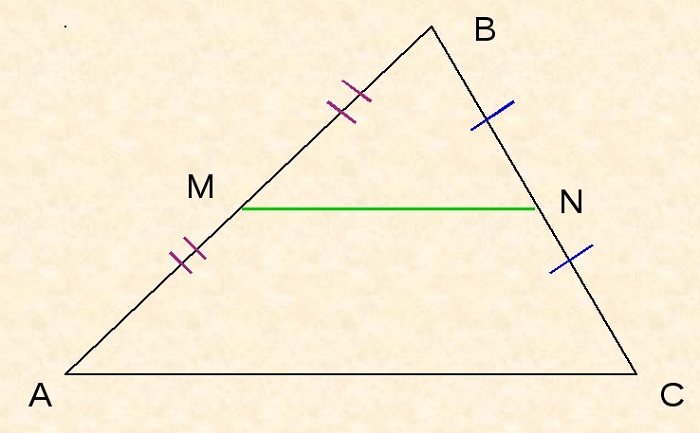
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.

По определению, MN – средняя линия ΔABC.

Необходимо доказать, что MN II AC, MN = ½AC.

Доказательства

Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.

Следовательно, MN II AC.

Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.

Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.

Рассматриваются треугольники MBN и ABC. В них угол B является общим,

По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.

Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.

Формула MN = ½AC следует из условий

поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.

Рассматривается сумма векторов

Поскольку в результате образуется замкнутая ломаная, то

Отсюда следует, что

Из последнего равенства следуют условия теоремы.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Следствия из теоремы с доказательствами

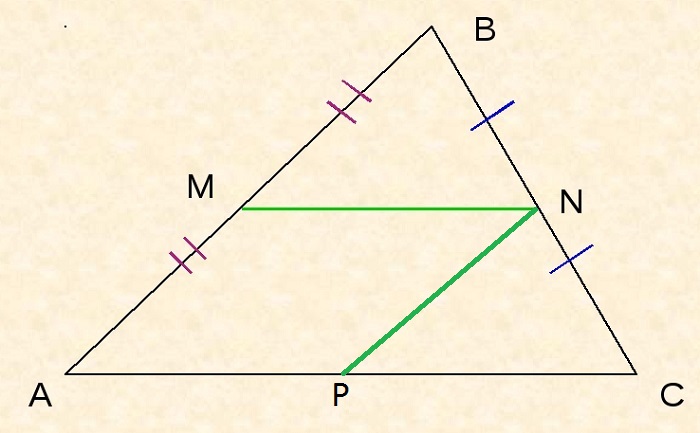
Следствие №1

Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому

Из третьего признака подобия вытекает рассматриваемое свойство.

Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как

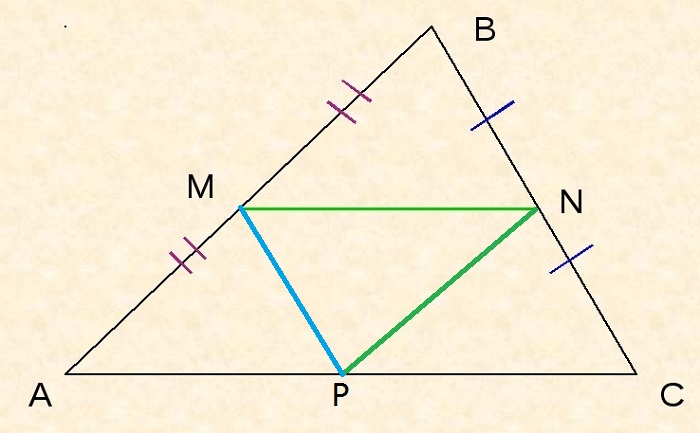
Следствие №2

Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.

Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.

Таким образом: ∠BNM = ∠BCA = ∠MPA.

Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.

Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.

Равенство остальных пар треугольников доказывается аналогично.

По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.

Видео:9 класс, 18 урок, Скалярное произведение векторовСкачать

Свойства средней линии треугольника

Теорема и следствия из неё составляют основные свойства средней линии треугольника.

Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.

Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.

Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.

Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Средняя линия прямоугольного треугольника

Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.

Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.

Видео:8 класс, 49 урок, Средняя линия трапецииСкачать

Пример решения задачи

Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.

Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.

Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.

Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.

Видео:Задача 5. Компланарны ли векторы a, b, c.Скачать

Что такое средняя линия треугольника

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

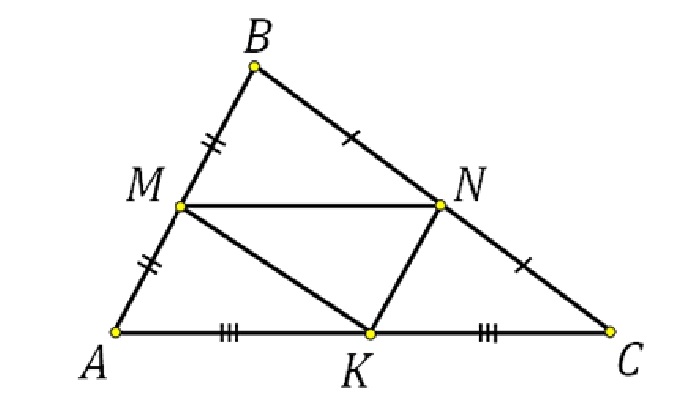
Определение средней линии треугольника

Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

KL – средняя линия треугольника ABC
K – середина стороны AB: AK = KB
L – середина стороны BC: BL = LC

Видео:Геометрия 9. Подготовка к КР по теме ВекторыСкачать

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:

Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:

△KBL ∼ △ABC (подобие по пропорциональности всех сторон)
Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL.
S_△ABC = 4 ⋅ S_△KBL

Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.

Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

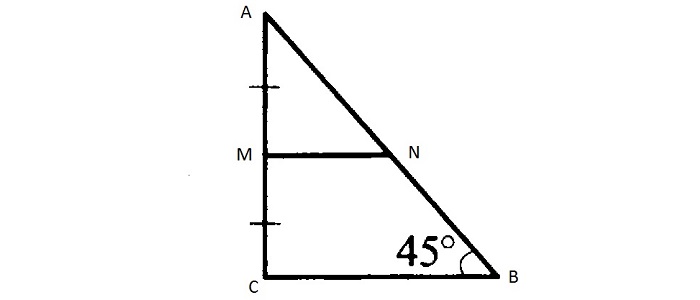
Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.