Каждая координата вектора равна (6 видео)

Векторы

Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется вектором.

Вектор с началом в точке A и концом в точке B обозначают $↖$ или строчной (маленькой) буквой, например $↖$

Любая точка плоскости является вектором. В этом случае вектор называется нулевым.

Модуль (длину) вектора обозначают $|АВ|↖$.

Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Два коллинеарных вектора называются сонаправленными, если они направлены в одну сторону.

Векторы называются равными , если они сонаправлены и их длины равны.

Сумма векторов — это вектор, который можно получить двумя способами.

Правило треугольника (А)
Правило параллелограмма (Б)

Для любых векторов $a↖, b↖, c↖$ справедливы равенства:

Разность векторов тоже можно получить двумя способами:

Если надо найти разность двух векторов, их необходимо отложить из одной точки. Результирующий вектор направлен к уменьшаемому.

Для любых $a↖$ и $b↖$ справедливо равенство $a↖-b↖=a↖+(↖)$

Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними.$a↖⋅b↖=|a↖|·|b↖|·cos⁡α$

Ненулевые векторы $a↖$ и $b↖$ перпендикулярны, если их произведение равно нулю.

Содержание

Метод координат
Каждая координата вектора равна одноименных координат его конца и. Действительно. Рассмотрим вектор HP. Пусть Р(х; у) и Р(х; у). Векторы ОН и являются радиус
Ваш ответ
решение вопроса
Похожие вопросы
Координаты вектора в математике
Координаты вектора
Свойства координат вектора
💡 Видео

Видео:Геометрия 9 класс (Урок№8 - Связь между координатами вектора и координатами его начала и конца.)Скачать

Метод координат

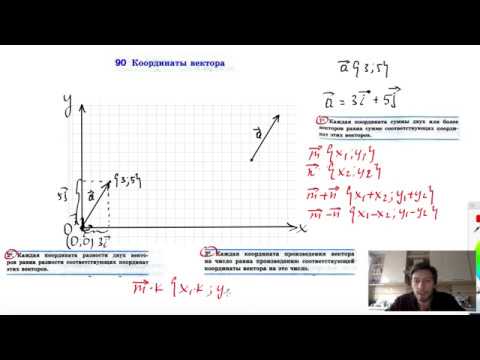
Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.

Для того чтобы векторы $a↖$ и $b↖$ были коллинеарными, необходимо и достаточно, чтобы выполнялось равенство $a↖=k·b↖$, где $k$ — это некоторое число.

Координаты середины вектора равны средним арифметическим координат его концов.

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Скалярное произведение векторов $a↖$ и $b↖$ в координатах находится по формуле $a↖·b↖= x1·x2+y1·y2$

Длина вектора $a↖$ вычисляется по формуле: $|a↖|=√$

Расстояние между двумя точками $M1(x1;y1)$ и $M2(x2; y2)$ находится по формуле $|M1M2|=√$

Найдите угол между векторами $a↖$ и $b↖$

Сначала нужно найти координаты векторов $a↖$ $b↖$
Найдем скалярное произведение векторов $a↖·b↖ = 2·8+6·4=16+24=40$
Найдем длины каждого вектора $|a↖|= √=√; |b↖|=√=√$
Найдем косинус угла между векторами $cosα=/<√·√>=/<√>=/=/$
Найдем угол $α=arccos/=45$

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Каждая координата вектора равна одноименных координат его конца и. Действительно. Рассмотрим вектор HP. Пусть Р(х; у) и Р(х; у). Векторы ОН и являются радиус

Видео:Координаты вектора. 9 класс.Скачать

Ваш ответ

Видео:Координаты точки и координаты вектора 1.Скачать

решение вопроса

Видео:Координаты вектора | Геометрия 7-9 класс #86 | ИнфоурокСкачать

Координаты вектора в математике

Координаты вектора ― это коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

Содержание:

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Координаты вектора

Для введения понятия координат вектора следует рассмотреть возможность разложения вектора по осям координат. Мы хотим каждый вектор задать парой чисел — проекциями этого вектора на оси координат. При таком подходе действия над векторами можно свести к действиям с парами чисел.

Определим проекции вектора на координатную ось. Пусть задана координатная ось Ох. Единичный отрезок ОЕ теперь будем считать единичным вектором , т. е. вектором, длина которого равна 1 (рис. 2.506).

Возьмем любой вектор и отложим его от некоторой точки А:

Спроектируем точки А и В на ось Ох. Получим точки и составляющую вектора по оси Ох (рис. 2.507). Ее длина со знаком «плюс» или «минус» и называют проекцией вектора на ось Ох.

Определение. Проекцией вектора на ось Ох называют длину его составляющей по этой оси, взятую со знаком «плюс» или «минус». При этом берется знак «плюс», если направление вектора совпадает с направлением оси Ох, и знак «минус», если эти направления противоположны. Если = 0, т. е.

Проекция точки — точка, проекция отрезка — отрезок (или точка), а проекция вектора — число.

Вектор получается из коллинеарного ему единичного вектора умножением на . При этом если сонаправлен с , то Если же противоположно направлен , то

Следовательно, имеет место равенство

Можно доказать следующие свойства проекций векторов на ось.

1. Равные векторы имеют равные проекции на заданную ось.

2. При сложении векторов их проекции на ось складываются.

3. При умножении вектора на число его проекция умножается на это число.

Прежде чем ввести понятие координат вектора, докажем теорему.

Теорема 6. Пусть на плоскости введена прямоугольная система координат с единичными векторами координатных осей Ох и Оу. Пусть — некоторый вектор, а — его проекции на оси координат. Тогда вектор единственным образом представляется в виде (рис. 2.508).

Выше получена формула для разложения вектора а по векторам (с учетом обозначения): .

Пару чисел называют координатами вектора в данной системе координат.

Координаты вектора в пространстве определяются так же, как на плоскости. Справедлива следующая теорема.

Теорема 7. Пусть в пространстве введена прямоугольная система координат с единичными векторами координатных осей Ох, Оу, Oz. Тогда вектор единственным образом представляется в виде (рис. 2.509).

Числа называются координатами вектора относительно векторов, которые называются базисными векторами или, короче, базисом.

Введенные координаты вектора позволяют получить формулу длины вектора.

Рассмотрим рисунок 2.508.

1. Если точка А не лежит на координатных осях, то треугольник прямоугольный.

2. (1, теорема Пифагора).

3. Так как то получаем, что (2).

4. Но поэтому

(3, 4).

Формула справедлива и в тех случаях, когда точка А лежит на какой-то оси координат.

Свойства координат вектора

В курсе геометрии нам практически не приходится работать с векторами в координатах (это приходится делать в курсе физики). Можно доказать различные свойства координат вектора:

1. Координаты равных векторов соответственно равны. Обратно: векторы, имеющие соответственно равные координаты, равны.

2. При сложении векторов их соответствующие координаты складываются. А именно, если

3. При умножении вектора на число его координаты умножаются на это число. А именно, если

Координаты вектора связаны с координатами точки по следующему правилу: чтобы найти координаты вектора, нужно от координат конца вектора отнять координаты начала вектора.

В частности, если вектор отложен от начала координат, то координаты вектора равны координатам его конца.

Возьмем в пространстве некую прямоугольную систему координат с началом в точке О и координатными осями х, у, z (рис. 2.510). Пусть А, В, С — точки с единичными координатами на этих осях, т. е. А(1, 0, 0), В(0, 1, 0), С(0, 0, 1).

Тогда векторы — это направляющие единичные векторы координатных осей х, у, z.