Какой четырехугольник называется ромбом сформулируйте особое свойство

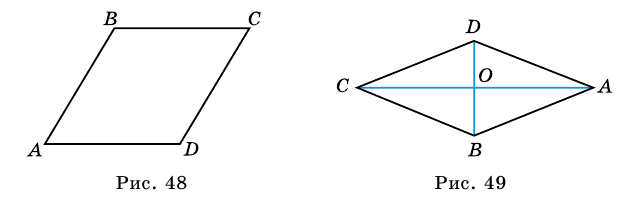
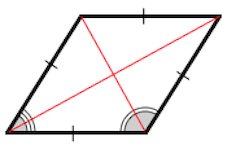
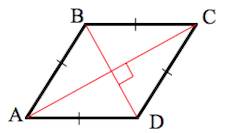
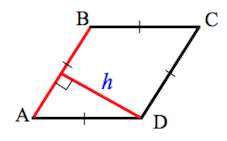
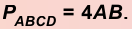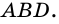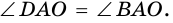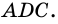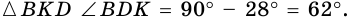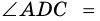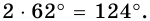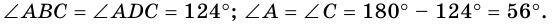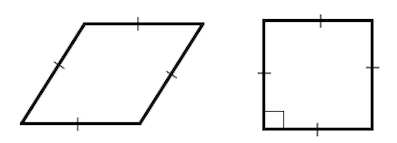Ромбом называют параллелограмм, у которого все стороны равны (рис. 48).

Так как ромб является параллелограммом, то он имеет все свойства параллелограмма.

1. Сумма любых двух соседних углов ромба равна 180°.

2. У ромба противолежащие углы равны.

3. Диагонали ромба точкой пересечения делятся пополам.

4. Периметр ромба

Кроме того, ромб имеет еще и такое свойство.

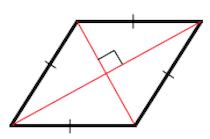
5. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Доказательство:

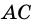
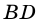
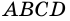
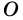
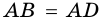
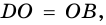
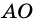
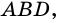
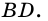
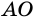
Пусть и — диагонали ромба (рис. 49), — точка их пересечения. Поскольку и то — медиана равнобедренного треугольника проведенная к основанию Поэтому является также высотой и биссектрисой треугольника

Следовательно, 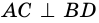и

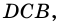
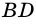
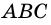
Аналогично можно доказать, что диагональ АС делит пополам угол а диагональ делит пополам углы и

Пример:

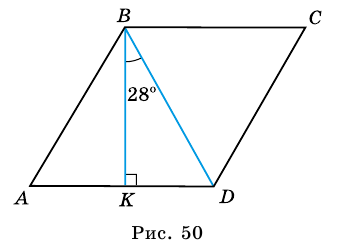
Угол между высотой и диагональю ромба проведенными из одной вершины, равен 28°. Найдите углы ромба.

Решение:

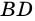
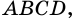
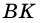
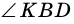
Пусть — диагональ ромба а — его высота (рис. 50), = 28°.

1) В

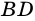
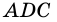
2) Так как делит угол пополам, то

3) Тогда

Ответ. 124°, 56°, 124°, 56°.

Рассмотрим признаки ромба.

Теорема (признаки ромба). Если в параллелограмме: 1) две соседние стороны равны, или 2) диагонали пересекаются под прямым углом, или 3) диагональ делит пополам углы параллелограмма, — то параллелограмм является ромбом.

Доказательство:

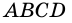
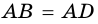
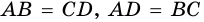
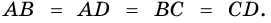
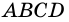
1) Пусть — параллелограмм (рис. 48). Так как (по условию) и (по свойству параллелограмма), то Следовательно, — ромб.

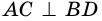
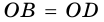
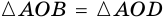
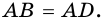
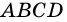
2) Пусть (рис. 49). Поскольку (по свойству параллелограмма), то (по двум катетам). Следовательно, По п. 1 этой теоремы — ромб.

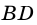
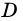
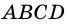
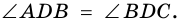
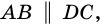
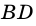
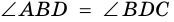
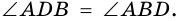
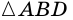
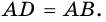
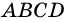
3) Диагональ делит пополам угол параллелограмма (рис. 49), то есть Так как — секущая, то (как внутренние накрест лежащие). Следовательно, Поэтому по признаку равнобедренного треугольника — равнобедренный и По п. 1 этой теоремы — ромб.

Пример:

Докажите, что если в четырехугольнике все стороны равны, то этот четырехугольник — ромб.

Доказательство:

Пусть 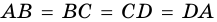(рис. 48).

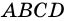
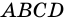
1) Так как противолежащие стороны четырехугольника попарно равны, то — параллелограмм по признаку параллелограмма.

2) У параллелограмма 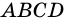соседние стороны равны. Поэтому — ромб (по признаку ромба).

Слово «ромб» греческого происхождения, которое в древние времена означало вращающееся тело, веретено, волчок. Ромб тогда связывали с сечением веретена, на которое намотаны нити.

В «Началах» Евклида термин «ромб» встречается единожды, а свойства ромба Евклид вообще не рассматривал.

• Квадрат и его свойства
• Трапеция и ее свойства
• Площадь трапеции
• Центральные и вписанные углы
• Четырехугольники и окружность
• Параллелограмм, его свойства и признаки
• Площадь параллелограмма
• Прямоугольник и его свойства

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Ромб. Свойства и признаки ромба

Ромб – это параллелограмм, у которого все стороны равны.

Если у ромба – прямые углы, то он называется квадратом.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Свойства ромба

1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.

Помимо этого:

2. Диагонали ромба перпендикулярны.

3. Диагонали ромба являются биссектрисами его углов.

4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Признаки ромба

Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:

1. Все стороны параллелограмма равны между собой ().

2. Диагонали пересекаются под прямым углом ().

3. Диагонали параллелограмма являются биссектрисами его углов.

Видео:Площадь ромба. Легче понять...Скачать

Площадь ромба

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Геометрические фигуры. Ромб.

Ромб — это параллелограмм с равными сторонами. Ромб с прямыми углами является квадратом.

Ромб рассматривают как вид параллелограмма, с двумя смежными равными сторонами либо с взаимно перпендикулярными диагоналями, либо с диагоналями делящими угол на 2 равные части.

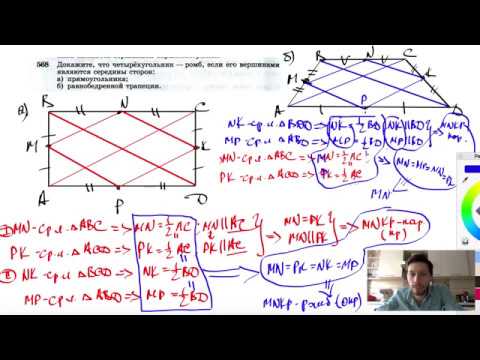
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать

Свойства ромба.

1. Ромб – это параллелограмм, поэтому противоположные стороны имеют одинаковую длину и параллельны попарно, АВ || CD, AD || ВС.

2. Угол пересечения диагоналей ромба является прямым (AC ⊥ BD) и точкой пересечения делятся на две одинаковые части. То есть диагонали делят ромб на 4 треугольника — прямоугольных.

4. Сумма квадратов диагоналей равняется квадрату стороны, умноженному на четыре (вывод из тождества параллелограмма).

Видео:Ромб. 8 класс.Скачать

Признаки ромба.

Параллелограмм ABCD будет называться ромбом только в случае выполнения хотя бы одного из условий:

1. 2 его смежные стороны имеют одинаковую длину (то есть, все стороны ромба равны, AB=BC=CD=AD).

2. Угол пересечения диагоналей прямой (AC⊥BD).

3. 1-на из диагоналей делит углы, которые ее содержат пополам.

Пусть мы заранее не знаем, что четырёхугольник оказывается параллелограммом, однако известно, что все его стороны равны. Значит этот четырёхугольник является ромбом.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Симметрия ромба.

Ромб симметричен относительно всех своих диагоналей, зачастую его используют в орнаментах и паркетах.

Видео:РОМБ . §5 геометрия 8 классСкачать

Периметр ромба.

Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры. У периметра та же размерность величин, что и у длины.

Периметр ромба равняется сумме четырех длин его сторон либо произведению длины всякой из его стороны на 4 (т.к. у ромба все стороны равны).

🎦 Видео

Ромб, признаки. 8 класс.Скачать

Миникурс по геометрии. ЧетырехугольникиСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Четырехугольники. Вебинар | МатематикаСкачать

8 класс, 8 урок, Ромб и квадратСкачать

Геометрия Признак ромба Если диагонали параллелограмма перпендикулярны, то этот параллелограмм ромбСкачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

8 класс, 4 урок, ПараллелограммСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Доказательство первого признака параллелограммаСкачать