Какие из следующих утверждений верны в любой четырехугольник можно вписать окружность если стороны (7 видео)

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

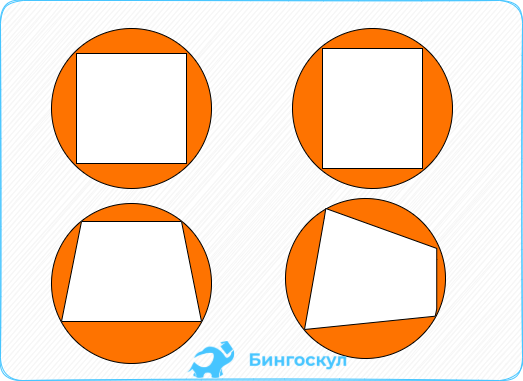
Окружность, точно можно вписать в такие геометрические фигуры, как:

Треугольник
Выпуклый, правильный многоугольник
Квадрат
Равнобедренная трапеция
Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

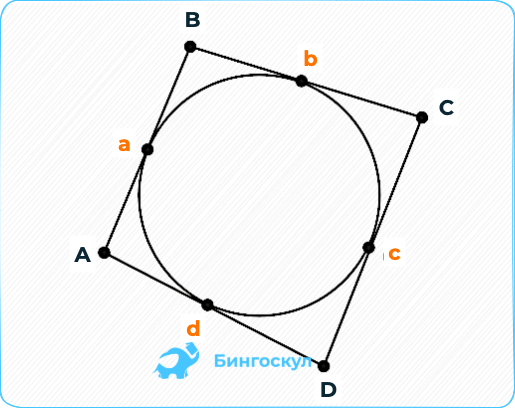
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Содержание

Свойства вписанной окружности
В треугольник
В четырехугольник
Примеры вписанной окружности
Верные и неверные утверждения
Окружность вписанная в угол
Какие из следующих утверждений верны в любой четырехугольник можно вписать окружность если стороны
Можно ли вписать четырёхугольник в окружность? Когда можно вписать?
Содержание:
Вписанный
Задача
В какой четырехугольник можно вписать окружность
Задача
📺 Видео

Свойства вписанной окружности

В треугольник

В любой треугольник может быть вписана окружность, причем только один раз.
Центр вписанной окружности — точка пересечения биссектрис треугольника.
Вписанная окружность касается всех сторон треугольника.
Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

Не во всякий четырехугольник можно вписать окружность.
Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито).
Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
Точка пересечения биссектрис — это центр вписанной окружности.
Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника.
Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

Треугольник
Четырехугольник
Многоугольник

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
Любой параллелограмм можно вписать в окружность. Неверное утверждение.
В любой четырехугольник можно вписать окружность. Неверное утверждение.
В любой ромб можно вписать окружность. Верное утверждение.
Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение.
Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение.
Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать

Какие из следующих утверждений верны в любой четырехугольник можно вписать окружность если стороны

Какие из данных утверждений верны? Запишите их номера.

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны.

2) В любой четырёхугольник можно вписать окружность.

3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны» — верно, по признаку параллельности прямых.

2) «В любой четырёхугольник можно вписать окружность» — неверно, поскольку в выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.

3) «Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника» — верно, по свойству треугольника.

Видео:Какие из СЛЕДУЮЩИХ УТВЕРЖДЕНИЙ верны? Решаем задание 19 из ОГЭ, 4 частьСкачать

Можно ли вписать четырёхугольник в окружность? Когда можно вписать?

Содержание:

Почти в любой четырехугольник можно вписать окружность. Трапеция, прямоугольник и квадрат для этого подходят всегда, тогда как сложные геометрические фигуры с четырьмя углами вписываются в круг избирательно. Рассмотрим условия, при которых 4-угольник может касаться точек на окружности всеми вершинами.

Видео:Если в четырёхугольник можно вписать окружностьСкачать

Вписанный

Вписанной называется фигура, вершины которой располагаются на окружности. Все треугольники и правильные 4-угольники, вроде квадрата и прямоугольника, размещаются внутри круга, причём их вершины совмещаются с точками на окружности. Вокруг неправильной фигуры с четырьмя углами не всегда можно описать круг. Разбираемся, какие условия нужно выполнить для решения проблемы.

У квадрата и прямоугольника все углы прямые – равны 90°, но это не ключ к разгадке. Случай с параллелограммом тому подтверждение. Чем примечательны прямоугольные 4-угольники? Может дело в сумме углов?

Трапеция в круг вписывается, но только равнобедренная. Одно из её свойств – сумма внутренних углов равна 360°, а соседних – 180°. Получается, что четырехугольник можно вписать в окружность, если сумма противоположных углов равняется 180°. Проверим на практике.

Помните: правило применимо только для выпуклых фигур, расположенных по одну сторону от проходящих через все стороны прямых.

Выпуклый дельтоид вписывается в круг, когда имеет пару прямых углов – называется прямоугольным.

Задача

Известны величины двух соседних углов вписанного четырёхугольника: 65° и 83°. Вычислить размеры сразу большего, затем – меньшего из оставшихся.

Известно, что сумма противоположных углов указанной геометрической фигуры равняется 180°. Отнимем от значения сначала большую цифру, затем – меньшую, чтобы выполнить условия задачи – найти неизвестные значения в указанном порядке.

180 – 65 = 115° – больший угол, 180 – 83 = 97° – меньший.

Видео:В любой четырёхугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

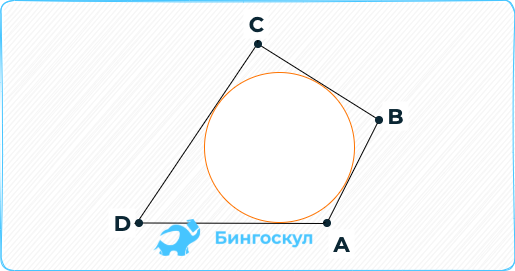
В какой четырехугольник можно вписать окружность

Описанным называют 4-угольник, стороны которого касаются круга. Существует теорема, показывающая, когда в четырехугольник можно вписать окружность: сумма его противоположных сторон должна быть одинаковой: AB + CD = BC + AD. В случае с прямоугольником условие не выполняется.