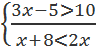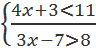Пусть а множество четырехугольников

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами.

Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) Ù В(х). С появлением этого предложения возникает вопрос, как найти его множество истинности, зная множества истинности высказывательных форм А(х) и В (х). Другими словами, при каких значениях х из области определения Х высказывательная форма А(х)ÙВ(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить Т_А – множество истинности предложения А(х), Т_В – множество истинности предложения В(х), а множество истинности их конъюнкции Т_А˄В, то, по всей видимости, Т_А˄В = Т_А Т_В.

Докажем это равенство.

1. Пусть а — произвольный элемент множества Х и известно, что а ∈ Т_А˄В. По определению множества истинности это означает, что высказывательная форма А(х)˄В(х) обращается в истинное высказывание при х = а, т.е. высказывание А(х)˄В(х) истинно. Так как данное высказывание конъюнкция, то, по определению конъюнкции, получаем, что каждое из высказываний А(а) и В(а) также истинно. Это означает, что а ∈Т_А и а ∈ Т_В. Следовательно, по определению пересечения множеств, а ∈ Т_А Т_В. Таким образом, мы показали, что Т_А˄В∈Т_А Т_В.

2. Докажем обратное утверждение. Пусть а – произвольный элемент множества Х и известно, что а ∈ Т_А Т_В. По определению пересечения множеств это означает, что а ∈ Т_А и а ∈ Т_В, откуда получаем, что А(х) и В(х) – истинные высказывания, поэтому конъюнкция высказываний А(х)˄В(х) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х)˄В(х), т.е. а ∈ Т_А˄В. Таким образом, мы доказали, что Т_А Т_В ∈ Т_А˄В.

Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства Т_А˄В = Т_А Т_В, что и требовалось доказать.

Заметим, что полученное правило справедливо и для высказывательных форм, содержащих более одной переменной.

Приведем примериспользования этого правила. Найдем множество истинности конъюнкции двух неравенств 2х > 10 и 4+х 10 ˄ 4+х 10, а Т₂ – множество решений неравенства 4+х

Рассматривая конъюнкцию и дизъюнкцию высказывательных форм, мы установили их тесную связь с пересечением и объединением множеств.

С другой стороны, характеристические свойства элементов пересечения и объединения множеств А и В представляют собой соответственно конъюнкцию и дизъюнкцию характеристических свойств данных множеств:

А B = , А B = , причем каждое свойство представляет собой высказывательную форму.

Упражнения

1. Покажите, что, выполняя следующие задания, мы находим множество истинности конъюнкции и дизъюнкции высказывательных форм:

а) Даны числа: 31,53,409,348,20,3094,233,33,271,143,3,333,14,30.

Выпишите все числа, в записи которых:

1) три цифры и есть цифра 3;

2) три цифры или есть цифра 3.

б) Из ряда 25, 12, 17, 5, 15, 36 выпишите те числа, которые:

1) двузначные или меньше 17;

2) двузначные и меньше 17.

в) Из ряда 72,312,522,483,1137 выпишите те числа, которые:

1) делятся на 3 и 9;

2) делятся на 3 или на 9.

2. Выполните следующие задания и дайте обоснование предложенным ответам:

а) Постройте по два треугольника, принадлежащих множеству А, если оно состоит из:

1) прямоугольных и равнобедренных треугольников;

2) прямоугольных или равнобедренных треугольников.

б) Постройте два четырехугольника, у которых:

1) диагонали равны и есть прямой угол;

2) диагонали равны или есть прямой угол.

в) Запишите три числа, которые:

1) делятся на 4 и больше 12;

2) делятся на 4 или 12.

3. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество ее решений с точки зрения логики:

а)

б)

4. Решите уравнение (х-3)×(х+2) ×(х-7)=0, х ∈ R. Использовалось ли вами понятие дизъюнкции высказывательных форм?

5. Вместо многоточия вставьте «и» либо «или»:

а) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

б) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

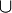
6. Пусть А – множество ромбов, В – множество прямоугольников. Как называется четырехугольник, являющийся одновременно ромбом и прямоугольником? Как можно выразить множество К таких четырехугольников через множества А и В?

Видео:Множество. Элементы множества. 5 класс.Скачать

Алгебра. 8 класс

Даны множества А = , В = и С = . Установите соответствие между множествами и наборами элементов, из которых они состоят

Впишите верный ответ.

Пусть С – множество прямоугольников, а D – множество ромбов. Какие фигуры принадлежат множеству ?

Укажите правильный ответ.

Пусть M – множество двузначных чисел, а N – множество натуральных чисел, кратных 7. Из каких элементов состоит множество ?

Даны два множества. Первое множество состоит из букв слова «пот»,
а второе из букв слова «кот». Укажите все верные утверждения.

Из букв, входящих в объединение указанных множеств, можно составить слово «крот».

Из букв, входящих в пересечение указанных множеств, можно составить слово «то».

Из букв, входящих в объединение указанных множеств, можно составить слово «поток».

Из букв, входящих в пересечение указанных множеств, можно составить слово «поток».

Установите соответствие между множествами и их изображениями с помощью кругов Эйлера.

Укажите верное утверждение.

Нельзя начертить два треугольника, пересечением которых будет четырехугольник.

Пересечение множеств точек прямых у = 1 и х = 2 состоит из двух точек.

Объединение множества параллелограммов и множества трапеций включает в себя все возможные виды четырехугольников.

Пересечение множества равносторонних треугольников и прямоугольных треугольников пусто.

Укажите все верные утверждения.

Пересечение множества чисел, кратных 2, и множества чисел, кратных 9, является множеством чисел, кратных 18.

Пересечение множества целых чисел, кратных 7, и множества чисел, кратных 21, содержит числа, кратные 3.

Объединение множеств отрицательных и положительных целых чисел является множеством всех целых чисел.

Объединение множеств цифр, используемых в записи чисел 24523 и 42563, состоит из пяти элементов.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Пусть А множество натуральных чисел , кратных 4, B множество натуральных чисел , кратных 6 ?

Математика | 5 — 9 классы

Пусть А множество натуральных чисел , кратных 4, B множество натуральных чисел , кратных 6 .

Назовите несколько элементов множества А пересечения с B .

Укажите наименьший элемент этого множества .

Как его называют ?

Это будут те числа которые кратны и 4 и 6 одновременно.

Например это числа :

12, 24, 36, 48, 60, 72.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Опишите множество которое является пересечением множеств А и В если : А — множество простых чисел В — множество четных чисел ; А — множество чисел кратных 9 В — множество чисел кратных 21?

Опишите множество которое является пересечением множеств А и В если : А — множество простых чисел В — множество четных чисел ; А — множество чисел кратных 9 В — множество чисел кратных 21.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ?

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ!

Даны множества А, В, С.

Изобразите отношения между ними.

Укажите характеристическое свойство множеств АUВ, А∩С, А В, А ∩ (В С) : № 11.

А – множество учащихся в школе ;

В – множество девочек в школе ;

С – множество учащихся третьих классов в этой школе.

А – множество натуральных чисел ;

В – множество натуральных чисел, кратных 5 ;

С – множество натуральных чисел, кратных 4.

А – множество параллелограммов ;

В – множество четырехугольников ;

С – множество прямоугольников.

А – множество прямоугольников ;

В – множество четырехугольников ;

С – множество квадратов.

А – множество треугольников ;

В – множество прямоугольных треугольников ;

С – множество равнобедренных треугольников.

А – множество трапеций ;

В – множество параллелограммов ;

С – множество четырехугольников, имеющих прямой угол.

А – множество прямоугольных треугольников ;

В – множество равносторонних треугольников ;

С – множество равнобедренных треугольников.

А – множество натуральных чисел, кратных 5 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 4.

А – множество натуральных чисел, кратных 2 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 5.

А – множество параллелограммов ;

В – множество квадратов ;

С – множество ромбов.

Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Являеться ли А подможеством В, если : 1)А — множество натуральных четных чисел, В — множество натуральных чисел?

Являеться ли А подможеством В, если : 1)А — множество натуральных четных чисел, В — множество натуральных чисел.

2)А — множество делителей числа 12, В — множество делителей числа 18.

3)А — множество чисел кратных 3, В — множество чисел кратных 6.

4)А — множество квадратов, В — множество прямоугольников.

5)А — множество треугольников, В — множество многоугольников.

Всем большое спасибо.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Пусть A — множество двузначных чисел, кратных числу 11?

Пусть A — множество двузначных чисел, кратных числу 11.

Запишите множество A

перечислением его элементов.

Видео:Четырёхугольник и его элементы – 8 класс геометрияСкачать

Задача?

А) Пусть А — множество натуральных делителей числа 18, B — множество натуральных делителей числа 24.

Запишите множество А∩В.

Укажите наибольший элемент этого множества.

Как его назвают?

Б) Пусть А — множество натуральных чисел, кратных 4, В — множество натуральных чисел, кратных 6.

Назовите несколько элементов множество А∩В.

Укажите наименьший элемент этого множества.

Как его назвают?

Видео:Четырехугольники №1 в ЕГЭ | Профильная математика ЕГЭ 2024 | УмскулСкачать

Помогите с домашнией работой?

Помогите с домашнией работой.

Пусть А — множество кратных числа 12, а В — множество кратных числа 15.

Запиши множества А и В с помощью фигурных скобок и найди их пересечение.

Назови наименьшее общее кратное чисел 12 и 15.

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

А)Пусть А — множество натуральных делителей числа 18, В — множество натуральных делителей числа 24?

А)Пусть А — множество натуральных делителей числа 18, В — множество натуральных делителей числа 24.

Запишите множество АnB.

Укажите наибольший элемент этого множества.

Как его называют?

Видео:Симедиана. Гармонические четырехугольники. | Олимпиадная математикаСкачать

Ничего не понимаю) помогите)) а — множество букв гласных звуков русского языка, в — множество натуральных четных однозначных чисел Укажите элементы каждого множества и найдите пересечения и объединени?

Ничего не понимаю) помогите)) а — множество букв гласных звуков русского языка, в — множество натуральных четных однозначных чисел Укажите элементы каждого множества и найдите пересечения и объединения этих множеств.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Множество чисел кратных трем и пяти, которые входят в множество натуральных чисел меньше 50?

Множество чисел кратных трем и пяти, которые входят в множество натуральных чисел меньше 50.

Видео:11 класс, 44 урок, Описанный четырехугольникСкачать

В — множество натуральных однозначных чисел?

В — множество натуральных однозначных чисел.

Запишите множество В перечислением его элементов.

На этой странице сайта, в категории Математика размещен ответ на вопрос Пусть А множество натуральных чисел , кратных 4, B множество натуральных чисел , кратных 6 ?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Х км — расстояние от А до В 0, 3х — проехал за первый час (0, 3х + 4) — проехал за второй час 60 км — осталось х — 0, 3х — (0, 3х + 4) = 60 х — 0, 3х — 0, 3х — 4 = 60 0, 4х = 60 + 4 0, 4х = 64 х = 64 : 0, 4 х = 160 км — расстояние от А до В.

66 / 77 = 0, 857142 7 / 8 = 0, 875 66 / 77 больше чем 7 / 8.

Значит мы сравниваем и . А теперь внимание! Когда нам дают дроби, например, 1 / 2 и 2 / 3, 2 / 3 и 3 / 4, 5 / 6 и 6 / 7, не нужно находить их общий знаменатель. Просто запомните, что дробь, у которой и числитель, и знаменатель больше на 1. Боль..

Наименьшее значение lxl = 0 ⇒ наибольшее значение (13 — lxl) = 13 ⇒ наибольшее значение (13 — lxl) / 6, 5 = 13 / 6, 5 = 2.

1) а) = 3 б) = 5 в) = 4 г) = 5 2 посмотри по таблице 3³ = 27 5³ = 125 2. А) = ³√(2 * 500) = ³√1000 = 10 б) = 4√(324 * 4) = 4√1296 = 6 в) = ∛54 2 = ∛27 = 3 3. Внизу.

135 — 16 = 119 119÷2 = 59, 5 — первое число 59, 5 + 16 = 75, 5 — второе число 75, 5 + 59, 5 = 135.

2 9 * (1, 8m — 5, 4) — 3 7 * (2, 1m — 4, 2) = 0, 4m — 1, 2 — 0, 9m + 1, 8 = 0, 6 — 0, 5m.

2 / 9 * (1, 8m — 5. 4) — 3 / 7 * (2. 1m — 4. 2) = = 2 / 9 * 18 / 10 * m — 2 / 9 * 54 / 10 — 3 / 7 * 21 / 10 * m — 3 / 7 * ( — 42 / 10) = = (2 * 2) / 10 * m — (2 * 6) / 10 — (3 * 3) / 10 * m + (3 * 6) / 10 = = 0. 4m — 1. 2 — 0. 9m + 1. 8 = = — ..

Вот формулы надеюсь помог Удачи.

5 дней. 7х3 м участок. 21 м² — 1м² (дерево) = 20 м² 20 : 4 м² (в день) = 5 дней.

🔥 Видео

Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

Гармония четырехугольников (feat. МО из Школково)Скачать

Миникурс по геометрии. ЧетырехугольникиСкачать

Четырехугольники. Вебинар | МатематикаСкачать

А.5.3 Четырехугольники (+ Д/З)Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Все типы 24 задание 2 часть ОГЭ ПО МАТЕМАТИКЕ 2023 УмскулСкачать

Свойство и признак вписанного четырехугольникаСкачать