Вопрос по алгебре:
1. Плоскость, притом только одна, проходит через а) две пересекающиеся прямые; б) одну прямую; в) две скрещивающиеся прямые.
2. Точка М лежит вне плоскости четырехугольника АВСД. Плоскости МАВ и МВС пересекаются по прямой
. М а) МА;
А В б) МВ;
в) МС;
г) АВ.
3. Точки А, В, С и Д не лежат в одной плоскости, следовательно
а) какие-то три из них лежат на одной прямой;
б) никакие из трех данных точек не лежат на одной прямой;
в) прямые АВ и СД пересекаются.
4. Точки А, В, С лежат на одной прямой, точка D не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных
плоскостей при этом получилось?
а) 2; б) 3; в) 1; г) бесконечно много.
5. Назовите общую прямую плоскостей AFD и DEF.
а) AD; б) DE; в) DF; г) AF.
6. Прямая а лежит в плоскости α и пересекает плоскость β. Каково взаимное расположение плоскостей α и β?
а) они совпадают;
б) имеют только одну общую точку;
в) не пересекаются;
г) пересекаются по некоторой прямой.
7. Если через две параллельные прямые проходят пересекающиеся плоскости, то линия их пересечения
а) параллельна каждой из двух прямых или совпадает с одной из них;
б) пересекается хотя бы с одной из этих прямых;
в) скрещивается хотя бы с одной из прямых.
8. Выберите верное утверждение.
а) Две прямые называются параллельными, если они не имеют общих точек;
б) две прямые, параллельные третьей прямой, параллельны;
в) две прямые, перпендикулярные третьей прямой, параллельны;
г) если углы равны, то их стороны соответственно сонаправлены.
9. Через вершину А параллелограмма ABCD и точку М, не лежащую в плоскости параллелограмма, проведена прямая АМ. Чему равен угол между прямыми АМ и ВС, если угол MAD равен 120˚?
а) определить нельзя; б) 120˚; в) 30˚; г) 60˚; д) 150˚.
10. Точка К не лежит в плоскости треугольника ВДС, точки А, М, и Р – середины отрезков КВ, КД, КС соответственно. Каково взаимное расположение плоскостей ВДС и АМР ?
а) плоскости параллельны; б) плоскости пересекаются; в) их расположение определить нельзя.
11. В кубе АВСДА1В1С1Д1 точка Е лежит на ребре АА1, а точка К – на ребре АВ Точка пересечения прямой ЕК с плоскостью грани ВВ1С1С лежит на прямой а) ВС; б) В1С1; в) ВВ1; г) СС1.
12. Прямая а параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая а параллельна любой прямой, лежащей в плоскости α;
б) прямая а не пересекает ни одну прямую, лежащую в плоскости α;
в) прямая а скрещивается со всеми прямыми плоскости α;
г) прямая а имеет общую точку с плоскостью .
13. В треугольнике АВС точки F и E принадлежат сторонам СВ и АВ соответственно, причём ВЕ : ЕА = 2 : 3. Через эти точки провели плоскость, параллельную АС. Найдите отношение BF : FC.
а) 3 : 2; б) 2 : 3; в) 3 : 5; г) 2 : 5.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Параллельность прямых и плоскостей (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
Т1 Параллельность прямых и плоскостей
Задачи для внеаудиторной самостоятельной деятельности:
3. Дан треугольник ABC и точка М, не принадлежащая его плоскости. Через М и А проведите плоскость а так, чтобы линия пересечения плоскостей ABC и а: 1) разделила [ВС] пополам; 2) разделила угол ВАС пополам.
4. Дана прямая а и точка М. Через данную точку проведите прямую, пересекающую а под прямым углом.
5. Докажите, что середины ребер AD, АВ, BCt CD тетраэдра ABCD принадлежат одной плоскости. Вершинами какого четырехугольника служат эти точки?
6. Даны две различные прямые а и Ь. Через данную точку М проведите прямую, скрещивающуюся с каждой из данных прямых, если известно, что данные прямые: 1) параллельны; 2) пересекаются.
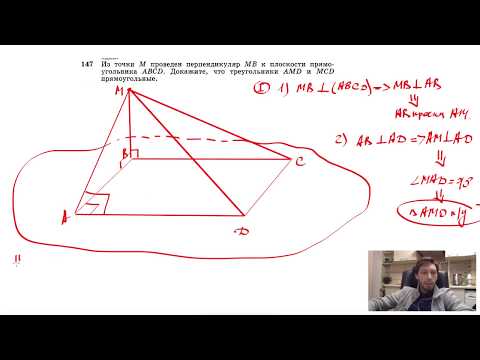
Видео:№147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать
7. Даны скрещивающиеся прямые а и b, прямая с пересекает каждую из данных прямых. Докажите, что любая прямая, параллельная с и отличная от этой прямой, скрещивается, по крайней мере с одной из прямых а и b.
8. Дано: а и b – скрещивающиеся прямые, С принадлежит а. Докажите, что плоскость, проходящая через b и С, пересекает прямую а.
9. Даны скрещивающиеся прямые a, b и точка С. Каково взаимное расположение плоскостей, проведенных через а и С, b и С?
10. Дано: а и b – скрещивающиеся прямые. Через точку М, принадлежащую прямой а, проведите прямую, пересекающую а и скрещивающуюся с b.
11. Верно ли утверждение, что прямая, параллельная плоскости, не пересекает ни одной из прямых, лежащих в этой плоскости?
12. Плоскость b пересекает прямую а, параллельную плоскости а. Докажите, что плоскости а и b пересекаются.
13. Дано: а и b – скрещивающиеся прямые. Через прямую а проведите плоскость, параллельную прямой b.
14. (Устно.) 1) Одна из сторон параллелограмма принадлежит плоскости а. Как расположены по отношению к плоскости а остальные стороны?
2) Сторона АС треугольника ABC принадлежит плоскости а. Как расположена по отношению плоскости а прямая, проходящая через середины сторон АВ и СВ?
15. (Устно.) Дан куб ABCDA1B1C1D1 (рис. 1). Как расположено ребро AA1 по отношению граней BB1CC1 и CC1 D1D? Ребро DC по отношению граней ABCD и AA1B1В?
16. Из внешней точки А проведен к плос — кости а отрезок АВ (В Ì а). Он разделен точкой С в отношении 3:4 (от А к В), и отсюда проведен параллельно плоскости а отрезок CD. = 12 см. Через точку D проведен к плоскости а отрезок ADE (Е Ì а). Найти расстояние между точками В и Е.
Даны прямая а и не лежащая на ней точка А. Провести плоскость, проходящую через точку А и параллельную прямой а.
2) Даны параллельные прямые а и b. Провести через прямую а плоскость, параллельную прямой b.
18. Докажите, что все прямые, пересекающие две параллельные прямые, лежат в одной плоскости.
19. Докажите, что все параллельные прямые, пересекающие данную прямую, лежат в одной плоскости.
20. Докажите, что если плоскость пересекает одну из двух параллельных прямых, то она пересекает и вторую. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1 если АА1 =5м, ВВ1 = 7 м и отрезок АВ не пересекает плоскость.
21. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1 если АА1 =5м, ВВ1 = 7 м и отрезок АВ не пересекает плоскость.
22. Решите задачу 21, если отрезок АВ пересекает плоскость.
23. Дан параллелограмм ABCD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках А1, В1, С1, D1. Найдите длину отрезка DD1, если АА1 — а, ВВ1 = b, СС1 = с.
24. Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма.
25. Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и CD, AC и BD, AD и ВС, пересекаются в одной точке.
26. Через данную точку проведите прямую, параллельную каждой из двух данных пересекающихся плоскостей.
27. Докажите, что через любую из двух скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
28. Докажите, что если две плоскости, пересекающиеся по прямой a, пересекают плоскость а по параллельным прямым, то прямая a параллельна плоскости а.
29. Докажите, что если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и вторую.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

30. Даны две скрещивающиеся прямые. Как провести через них две параллельные плоскости?
31. Плоскости а и b параллельны плоскости у. Могут ли плоскости а и b пересекаться?
32. Плоскости а и b пересекаются. Докажите, что любая плоскость у пересекает хотя бы одну из плоскостей а, b.
33. Докажите, что все прямые, проходящие через данную точку параллельно данной плоскости, лежат в одной плоскости.
34. Через данную точку проведите плоскость, параллельную каждой из двух пересекающихся прямых. Всегда ли это возможно?
35. Докажите, что если параллелограммы ABCD и ABC1D1 лежат в разных плоскостях, то четырехугольник CDD1C1 тоже параллелограмм.
36. Через вершины параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость
1. Прямая EF, не лежащая в плоскости прямоугольника ABCD, параллельна стороне ВС (рис. 1). Докажите, что прямые EF и AD параллельны.
1. Ромб ABCD и трапеция BCMN (ВС — основание трапеции) не лежат в одной плоскости (рис. 1). Как расположены прямые MN и AD?
1. Треугольник ABC и трапеция АВКР (АВ — основание трапеции) не лежат в одной плоскости (рис. 1). Как расположены прямые РК и MN, где MN — средняя линия треугольника ABC?
2. Точка М лежит вне плоскости параллелограмма ABCD (рис. 2). Точки Р, F, Е, К соответственно середины отрезков MA, MB, MC, MD. Определите вид четырехугольника PFEK.
1. Треугольник ABC и трапеция АВКР не лежат в одной плоскости (рис. 1). MN — средняя линия треугольника ABC, MN = РК. Как расположены прямые МР и NK?
1. Прямые а и b лежат в одной плоскости. Могут ли прямые аи b: а) пересекаться; б) быть параллельными; в) скрещиваться?
3. Прямые а и b параллельны. Точки А и В принадлежат прямой а, точки С и D принадлежат прямой b. Лежат ли прямые АС и BD в одной плоскости?
2. Какое положение занимает прямая, лежащая на плоскости, относительно прямой, пересекающей эту плоскость?
3. Прямые а и Ь лежат соответственно в плоскостях а и b, которые пересекаются по прямой с. Прямые а и с, b и с параллельны. Что можно сказать о взаимном расположении прямых а и b?
1. Две параллельные прямые с и Ь соответственно параллельны прямым c и d. Как расположены прямые aиd?
2. Даны скрещивающиеся прямые а и b. Как может быть расположена прямая а относительно прямой с, если: а) с || b; б) прямые с и b пересекаются; в) прямые с и b скрещивающиеся?
3. Даны треугольник ABC и трапеция ABMD (АВ — основание трапеции), не лежащие в одной плоскости. Как расположены средние линии треугольника и трапеции?
2. Докажите, что все параллельные прямые, пересекающие данную прямую, лежат в одной плоскости.
2. Плоскости а и b пересекаются по прямой т. Прямая а лежит в плоскости a и пересекает плоскость b. Пересекаются ли прямые а и m? Почему?
2. Даны пересекающиеся плоскости а и b. Прямая а лежит в плоскости а и пересекает плоскость b в точке А. Прямая b лежит в плоскости b и пересекает плоскость а в точке В. Докажите, что АВ — линия пересечения плоскостей а и b.
1. В чем ошибка чертежа (рис. 9)? Дайте объяснение. Сделайте верный чертеж.
2. По данным рисунка 10 постройте:
1) точки пересечения прямой EF с плоскостями AВС и А1 В1С1;
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

2) линию пересечения плоскостей ADF и EFD;
3) линию пересечения плоскостей EFD и ABC.
1. На рисунке 1 плоскости а и b пересекаются по прямой EF. Прямая АВ лежит в плоскости а. В плоскости b через точку С провести прямую так, чтобы она:
2) была бы скрещивающаяся с прямой АВ;
3) была бы параллельна прямой АВ.
1. На рисунке 5 плоскости аиb пересекаются по прямой EF. Прямая АВ лежит в плоскости а и параллельна EF. В плоскости b через точку С провести прямую так, чтобы она:
2) была бы скрещивающейся с прямой АВ;
3) была бы параллельна прямой АВ.
2. Прямая b лежит в плоскости а. Прямая а не лежит в плоскости а и параллельна прямой b. Через точку М, лежащую в плоскости а (МÎb), проведена прямая с, параллельная а. Докажите, что с лежит в плоскости а.
Задачи на построение сечений, для внеаудиторной самостоятельной деятельности.
1. Докажите, что середины ребер AD, АВ, ВС, CD тетраэдра ABCD принадлежат одной плоскости. Вершинами какого четырехугольника служат эти точки?
2. Дан тетраэдр ABCD. Выберите в грани ABD точки М и N, а в грани ABC точку Р так, чтобы сечение тетраэдра плоскостью MNC было: 1) треугольником; 2) четырехугольником. Постройте эти сечения.
3. Дан тетраэдр ABCD; точки М и N принадлежат внутренней области треугольника ABC, точка Р принадлежит грани ABD. Постройте сечение тетраэдра плоскостью MNP.
4. Дан тетраэдр ABCD, точки М и N принадлежат соответственно ребрам AD и DC. Выберите точку Р в грани BCD так, чтобы сечение MNP было: 1) треугольником; 2) четырехугольником. Постройте эти сечения.
5. Дан тетраэдр ABCD. 1) Постройте его сечение плоскостью, проходящей через вершину D и внутреннюю точку М грани ABC и параллельной ребру АВ. 2) Вычислите площадь сечения, если все ребра тетраэдра имеют длину а, причем ÷СМ÷ : ÷MN÷ = 1, где NÎ[АВ].
Постройте сечение куба плоскостью, проходящей через середины М, N, Р попарно скрещивающихся ребер. 2) Найдите площадь сечения, если ребро куба равно а.
11. Дан параллелепипед ABCDA1 B1C1D1;точка М принадлежит грани ABCD. Постройте сечение параллелепипеда плоскостью:
1) проходящей через точку М и параллельной грани АВВ1А1;
12. В кубе ABCDA1B1C1D1 провести сечение: 1) через ребра AD и В1С1; 2) через ребро АВ и середину ребра DD1;3) через середины ребер АВ и ВС параллельно ребру ВВ1; 4) через середину ребра AA1 параллельно ребрам ВС и C1D1
13. В треугольной пирамиде SABC провести сечение через середину ребра АВ параллельно ребрам: 1) АС и AS; 2) BS и CS; 3) ВС и CS; 4) ВС и AS; 5) АС и ВS.
2. В параллелепипеде ABCDA1B1C1D1 основание ABCD—квадрат со стороной, равной 8 см, остальные грани — прямоугольники. Боковое ребро равно 3 см. Е — середина А1В1. Постройте сечение параллелепипеда плоскостью, проходящей через АС и точку Е, и найдите периметр сечения.
1. В тетраэдре DAВС точка М — середина AD, PÎDC и DP:PC = 1:3. Постройте сечение тетраэдра плоскостью, проходящей через точки М и Р и параллельно ВС. Найдите площадь сечения, если все ребра тетраэдра равны а.
1. Параллелограммы ABCD и ADFE лежат в разных плоскостях и имеют общую сторону AD. Прямая m, параллельная ВС, пересекает плоскости ABE и DCF соответственно в точках Н и Р. Докажите, что HPFE — параллелограмм.
2. Плоскости а и b параллельны, а||а1, (рис. 53). Прямая а пересекает плоскости а и b соответственно в точках А и В, а пря мая а1 пересекает плоскость а в точке А1. Постройте точку пересечения а1 с плоскостью b. Поясните.
3. В тетраэдре DABC ÐDBA = ÐDBC= 90°, DB=6, AB=ВС = 8, AС= 12. Постройте сечение тетраэдра плоскостью, проходящей через середину DB и параллельной плоскости ADC. Найдите площадь сечения.
Видео:№365. Вне плоскости параллелограмма ABCD взята точка О. Точка M — середина АВ, а точка КСкачать

1. Вне плоскости а расположен треугольник ABC, у которого медианы АА1 и ВВ1 параллельны плоскости ее. Через вершины В и С треугольника проведены параллельные прямые, которые пересекают плоскость а соответственно в точках Е и F. Докажите, что ECBF — параллелограмм.
2. Плоскости а и b параллельны (рис. 55). Прямая а пересекает плоскости а и b соответственно в точках А и В, а прямая b — в точках С и D, Найдите взаимное положение прямых а и b. Поясните.
3. Все грани параллелепипеда ABCDA1B1C1D1 квадраты со стороной а. Через середину ребра AD параллельно плоскости DA1B1 проведена плоскость. Найдите периметр сечения.
1. В каком случае три точки в пространстве не определяют положение плоскости, проходящей через эти точки?
2. Могут ли две различные плоскости иметь только одну общую точку?
3. Точка М не лежит на прямой а. Через точку М проводятся прямые, пересекающие прямую а. Лежат ли эти прямые в одной плоскости?
4. Каково взаимное положение прямых (рис. 61):
5. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b пересекаться?
6. Прямая а параллельна плоскости а. Существуют ли на плоскости а прямые, не параллельные а? Если да, то каково их взаимное положение?
10. Плоскость а пересекает только боковые ребра параллелепипеда. Определите вид сечения.
1. Что можно сказать о взаимном положении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой?
2. Могут ли две различные плоскости иметь только две общие точки?
3. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Лежат ли все эти прямые в одной плоскости?
5. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b быть параллельными?
6. Две прямые параллельны одной и той же плоскости. Можно ли утверждать, что эти прямые параллельны между собой? Если нет, то каково их взаимное положение?
7. Прямые m и n параллельны (рис. 65). Точки A и В соответственно принадлежат прямым m и п; b лежит в плоскости а, а||b. Каково взаимное положение прямых b и с?
8. Даны четырехугольник ABCD и плоскость а. Его диагонали АС и BD параллельны плоскости а. Каково взаимное положение АВ и плоскости а?
10. Плоскость а проходит через диагональ основания параллелепипеда и середину одной из сторон верхнего основания. Определите вид сечения.
1. Точки А, В, С и D не лежат в одной плоскости. Выберите верное утверждение:
а) прямая АВ параллельна прямой CD;
б) прямая АВ пересекает прямую CD;
в) прямая АС пересекает прямую BD;
г) прямые АС и BD — скрещиваются.
2. Сторона АВ треугольника ABC принадлежит плоскости a, точка D, не принадлежащая прямой АВ, — проекция точки С на плоскость а. Точка Т — середина АВ. Выберите верное утверждение:
а) прямые СТ и АВ не пересекаются;
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

б) прямые СТ и АВ параллельны;
в) прямые ВТ и AD пересекаются;
г) прямые AT и BD скрещивающиеся.
З. Через концы отрезка АВ, не пересекающего плоскость а и точку С — середину этого отрезка, проведены параллельные прямые, пересекающие плоскость а в точках А1, В1 и С1 соответственно. Найдите длину отрезка СС1, если АА1 = 12 см, а ВВ1 = 6 см.
б) 9 см; г) другой ответ.
4. Плоскость а, параллельная стороне ВС треугольника АВС, пересекает стороны АВ и АС в точках М и N соответственно. Найдите длину отрезка ВС, если MN равен 6 см, а АМ:МВ = 3:5.
а) 16 см; в) 12 см;
б) 4,8 см; г) другой ответ.
5.Через концы отрезка АВ и точку С этого отрезка проведены параллельные прямые, пересекающие некоторую плоскость а в точках А1, B1 и С1 соответственно. Найдите длину отрезка CC1 если АА1 равен 6 см, ВВ1 равен 13 см, a АС:СВ = 2:5. Отрезок АВ не пересекает плоскость а.
б) 7 см; г) другой ответ.
6.Точки М, N и Р — параллельные проекции точек А, В и D на плоскость а, причем точка D принадлежит отрезку АВ. Найдите АВ, если: MN = 12см, NP = 8см, а BD = 14см.
а) 21 см; в) 24 см;
б) 28 см; г) другой ответ.
7. Выберите верное продолжение фразы: проекция трапеции на плоскость при параллельном проектировании может быть.
а) параллелограммом или трапецией;
б) только трапецией;
в) отрезком или трапецией;
г) ромбом или трапецией.
1. Точки A, В, С и D лежат в одной плоскости. Выберите утверждение, которое не может быть верным:
а) прямая АВ параллельна прямой CD;
б) прямая АВ пересекает прямую CD;
в) прямая АС пересекает прямую BD;
г) прямые АС и BD — скрещиваются.
2. Сторона KМ треугольника КМВ принадлежит плоскости а, точка Р, не принадлежащая прямой КМ, — проекция точки В на плоскость а. Точка N — середина MB. Выберите неверное утверждение:
а) прямые МР и NP пересекаются;
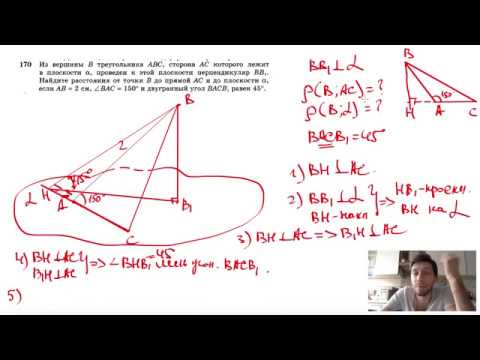
Видео:№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать
б) прямые MB и NP пересекаются;
в) прямые KB и NP пересекаются;
г) прямые КР и NP пересекаются.
3. Через концы отрезка MN, не пересекающего плоскость а, и точку К — середину этого отрезка проведены параллельные прямые, пересекающие плоскость а в точках M1, N1 и К1 соответственно. Найдите длину отрезка NN1,если ММ1 = 16 см, а КК1 = 9 см.
🌟 Видео
№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать

№23. Точка М не лежит в плоскости прямоугольника ABCD.Скачать

№54. Точка В не лежит в плоскости треугольника ADC, точки М, N и Р — середины отрезков ВА, ВССкачать
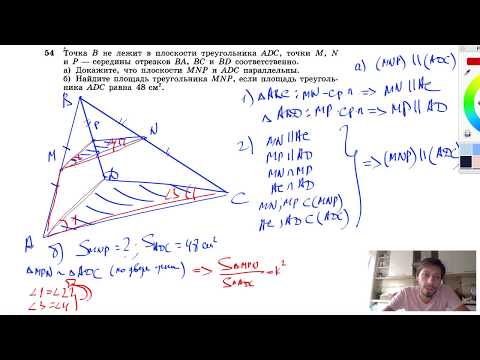
№24. Точка М не лежит в плоскости трапеции ABCD с основанием AD.Скачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Как строить сечения параллелепипедаСкачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

№42. Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости,Скачать
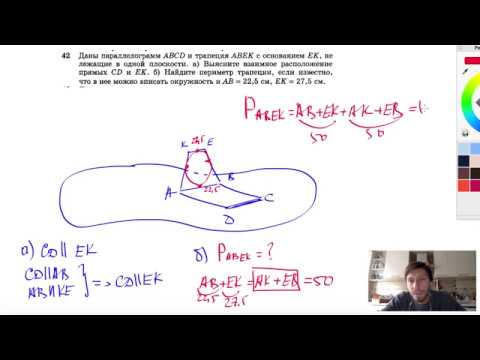
Стереометрия с нуля и до уровня ЕГЭ за 4 часа | Вся теория и задачи по №13 | Математика профильСкачать

Как строить сечения тетраэдра и пирамидыСкачать













