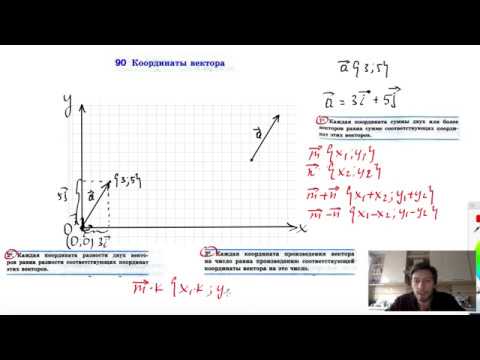
С понятием вектора мы встречаемся чаще,чем сами подозреваем. В данной работе я постаралась максимально изучить, в каких же сферах мы взаимодействуем с ним.
Просмотр содержимого документа
«Применение векторов в повседневной жизни»
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор. Далее, в процессе работы над данным проектом, я приведу ещё множество не менее интересных примеров векторов.
Вообще, я считаю, что математика – это интереснейшая наука, в познании которой нет границ. Я выбрала тему о векторах не случайно, меня очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, я думаю, что эта тема весьма актуальна. В психологии, биологии, экономике и многих других науках употребляют понятие «вектор». Подробнее об этом я расскажу позже.
Целями данного проекта являются приобретение навыков работы с векторами, умение видеть необычное в обычном, выработка внимательного отношения к окружающему миру.
История возникновения понятия вектор
Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.[2]
Векторы в математике
Вектором называется направленный отрезок, который имеет начало и конец.[1]




Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны.
Операции над векторами




В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

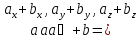

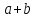


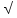
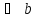
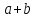

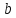
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:
Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же 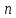

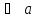
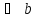
Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:




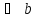
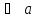
Умножение вектора на число


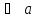

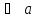
Скалярное произведение векторовСкалярное
Скалярным произведением называют число, которое получается при умножении вектора на вектор. Находится по формуле:

Скалярное произведение можно найти ещё через длину векторов и угол между ними. 
Применение векторов в смежных науках Векторы в физике Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Векторы в литературе Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу сил равна нулю. А сила, как известно, векторная величина. Векторы в химии
Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца.
Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».
Все прямые химических реакций проходят через начало координат. Любую прямую в пространстве нетрудно выразить векторами, но поскольку прямая химической реакции проходит через начало системы координат, то можно принять, что вектор прямой химической реакции находится на самой прямой и называется радиус-вектором. Начало этого вектора совпадает с началом системы координат. Таким образом, можно сделать вывод: любая химическая реакция характеризуется положением ее вектора в пространстве. Векторы в биологии
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы.
Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.
Векторы в экономике
Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора.
Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.
Векторы в психологии
На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов.
Векторы в повседневной жизни
Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора. А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время.
Векторы в знаках дорожного движения
Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителя. В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог.
Базовое понятие «вектор», рассмотренное нами ещё на уроках математики в школе, является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения.
Каждый человек постоянно сталкивается с векторами в повседневной жизни.
Векторы необходимы нам для изучения не только математики, но и других наук.
Видео:Координаты вектора в пространстве. 11 класс.Скачать

Статья по теме «Векторы в нашуй жизни»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:9 класс, 2 урок, Координаты вектораСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Координаты и векторы в нашей жизни
Для древних греков геометрия была неотделима от фигур. Решение задачи с плоскостями, прямыми или более сложными фигурами всегда сопровождалось чертежами. С помощью аналитической геометрии эти задачи можно решать «вслепую». Геометрические фигуры состоят из точек. Соотнесение этих точек с числами позволяет превращать геометрические задачи в алгебраические. Это достигается путем определения одно -, двух- или трехмерной системы координат в зависимости от того, работаем ли мы на прямой, на плоскости или в пространстве.
Почти все хотя бы раз в жизни играли в «морской бой» . Это игра, в которой соперники на листках в клетку закрашивают отдельные ячейки, создавая таким образом целую военную флотилию. Игроки скрывают друг от друга расположение своих судов и ведут разговоры такого плана:
На самом деле игроки передают друг другу координаты, на которых надеются обнаружить вражеский корабль. Его расположение обычно определяется координатами по горизонтали и вертикали . Таким образом, однопалубный корабль может находиться на клетке 3-Е, а четырехпалубное судно занимать клетки с координатами 2-В, 3-В, 4-В и 5-В. Выбор чисел или букв для обозначения той или иной координаты — вопрос чисто условный. Мы могли бы взять цифры для указания как на горизонтальную, так и на вертикальную координату; тогда местонахождение однопалубного судна определялось бы парой (3, 6). Такая система позволяет представить простой рисунок посредством пар чисел. Например, рисунок на иллюстрации справа можно представить следующей последовательностью числовых пар:
(2, 2), (3, 3) (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (6,3), (7,3), (8,3), (9, 2) и (9, 3).
Вектор — одно из основных геометрических понятий. Понятие вектора появилось в работах немецкого математика XIX в. Г. Грассмана и ирландского математика У. Гамильтона; затем оно было охотно воспринято многими математиками и физиками. Векторы применяются в классической механике Галилея — Ньютона (в ее современном изложении), в теории относительности, квантовой физике, в математической экономике и многих других разделах естествознания, не говоря уже о применении векторов в различных областях математики. Вектор — многозначный термин; величина, характеризующаяся размером и направлением. Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках.
Когда в товарищах согласья нет,
На лад их дело не пойдет,
И выйдет из него не дело, только мука.
Однажды Лебедь, Рак да Щука
Везти с поклажей воз взялись
И вместе трое все в него впряглись;
Из кожи лезут вон, а возу все нет ходу!
Поклажа бы для них казалась и легка:
Да Лебедь рвется в облака,
Рак пятится назад, а Щука тянет в воду.
Кто виноват из них, кто прав — судить не нам;
А правда, что воз и нынче там?
Если рассмотреть с точки зрения механики басню о том «как лебедь, рак да щука везти с поклажей воз взялись». Результат получается совсем не похожий на вывод баснописца Крылова.
Перед нами механическая задача на сложение нескольких сил, действующих под углом друг к другу. направление сил определено в басне так:
Лебедь рвется в облака, рак пятится назад, а щука тянет в воду.
Это значит, что одна сила, тяга лебедя, — направлена вверх; другая, тяга щуки, — вбок; третья, тяга рака, — назад. Не забудем, что существует еще и четвертая сила — вес воза, которая направлена отвесно вниз. Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех, приложенных к возу сил равна нулю.
Так ли это? Посмотрим. Лебедь, рвущийся к облакам, не мешает работе рака и щуки, даже помогает им: тяга лебедя направлена против силы тяжести, облегчая вес воза, а может быть даже и уравновешивает его, — ведь груз невелик («поклажа бы для них казалась и легка»). Допустив для простоты последний случай, мы видим, что остаются только две силы: тяга рака и тяга щуки. О направлении этих сил говорится, что «рак пятится назад, а щука тянет в воду». Само собой разумелось, что вода находится не впереди воза, а где-нибудь сбоку. Значит силы рака и щуки направлены под углом одна к другой. Если приложенные силы не лежат на одной прямой, то равнодействующая их никак не может равняться нулю.
Поступая по правилам механики строим на обеих силах ОВ и ОС параллелограмм, диагональ его OD дает направление и величину равнодействующей. Ясно, что эта равнодействующая сила должна сдивинуть воз с места, тем более, что вес его частично или полностью уравновешивается тягой лебедя. Другой вопрос в какую сторону сдивинется воз: вперед, назад или вбок? Это зависит уже от соотношения сил и угла между ними
Видео:Координаты вектора. 9 класс.Скачать

Векторы вокруг нас
С темой «Вектор» я познакомилась на уроке математики в 8-ом классе. Особого интереса она у меня не вызвала, но без неё я не могла изучать раздел физики «Механика» в 9-ом классе. После предпрофиля в 9-ом классе я решила продолжить обучение в 10-ом классе естественнонаучного профиля, где встретилась с векторами не только на физике уже в теме «Электричество», но и на химии, биологии и опять на математике, но уже в пространстве. Тогда я решила посмотреть, в каких ещё областях знаний можно встретить это понятие и насколько оно актуально в жизни.
Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| vektory.doc | 981.5 КБ |
Видео:11 класс, 2 урок, Координаты вектораСкачать

Предварительный просмотр:
НАЦИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
«ИНТЕЛЛЕКТУАЛЬНО-ТВОРЧЕСКИЙ ПОТЕНЦИАЛ РОССИИ»
Конкурс исследовательских работ «ЮНОСТЬ, НАУКА, КУЛЬТУРА-СЕВЕР»
Векторы вокруг нас
СОШ №8, 11 класс, г. Елизово, Камчатский край
Голованева Любовь Викторовна
учитель математики, высшая квалификационная категория,
почётный работник общего образования РФ,
победитель конкурса лучших учителей РФ
2008-2009 учебный год
- Введение 3
- Векторы в предметах естественнонаучного цикла 5
- Векторы вокруг нас 8
- Векторы в знаках дорожного движения 9
- Заключение 10
- Список литературы 11
- Приложение 12
ХХI ВЕК – век новых технологий и я, уже нынешняя одиннадцатиклассница, продолжаю усердно «грызть» гранит науки.
С темой «Вектор» я познакомилась на уроке математики в 8-ом классе. Особого интереса она у меня не вызвала, но без неё я не могла изучать раздел физики «Механика» в 9-ом классе. После предпрофиля в 9-ом классе я решила продолжить обучение в 10-ом классе естественнонаучного профиля, где встретилась с векторами не только на физике уже в теме «Электричество», но и на химии, биологии и опять на математике, но уже в пространстве. Тогда я решила посмотреть, в каких ещё областях знаний можно встретить это понятие и насколько оно актуально в жизни.
Проект назвала «Векторы вокруг нас». Я работала по следующим направлениям:
- «Векторы в предметах естественнонаучного цикла»
- «Векторы вокруг нас»
- «Векторы в знаках дорожного движения».
Я поставила перед собой цели:
- Проследить важность понятия «Вектор» в предметах естественно-научного цикла
- Рассмотреть при получении, каких специальностей будет происходить развитие понятия «вектор» в высшей школе.
- Обратить внимание одноклассников и окружающих на векторы вокруг нас.
Внимательно изучив различные материалы из книг, поработав в Интернете, я узнала, что понятие «Вектор» — относительно новое математическое понятие и его изучает раздел математики «Векторное исчисление».
Векторное исчисление, математическая дисциплина, в которой изучают свойства операций над векторами евклидова пространства. При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и направленностью (например, сила, ускорение, скорость).
Я проделала эксперименты по химии, посетила строящийся мост через реку Авача, прошла с фотоаппаратом по магазинам и улицам г. Елизова, проехала по дорогам Елизовского района и, используя собственные наблюдения, я пришла к выводу, что понятия вектора очень распространены, и мы буквально сталкиваемся с ними на каждом шагу. Кроме того, мне предстоит продолжить их изучение в высших учебных заведениях (например, в векторной алгебре). В жизни векторы помогают найти нужный объект, сэкономить время, они даже выполняют предписывающую функцию (в знаках дорожного движения), тем самым, предотвращая аварии на дорогах и сохраняя жизни участников движения.
Меня заинтересовала книга «Правила дорожного движения», а если конкретно, то:
- дорожные знаки и их значение;
- пешеходные переходы и места остановок маршрутных транспортных средств;
- обязанности пешеходов;
- обязанности пассажиров;
- дополнительные требования к движению велосипедистов, мопедов;
- таблица штрафов;
- оформление квитанции оплаты штрафов ГИБДД.
Векторы в предметах естественнонаучного цикла.
Возникновение векторного исчисления тесно связано с потребностями механики и физики. До XIX в. для задания векторов использовался лишь координатный способ, и операции над векторами сводились к операциям над их координатами. Лишь в середине XIX в. усилиями ряда учёных было создано векторное исчисление, в котором операции проводились непосредственно над векторами, без обращения к координатному способу задания .
Сам термин «вектор» впервые появился в 1845 году у английского математика и астронома Уильяма Гамильтона . Основы векторного исчисления были заложены исследованиями английского математика У. Гамильтона и немецкого математика Г. Грассмана. Их идеи были использованы английским физиком Дж. К. Максвеллом в его работах по электричеству и магнетизму. Современный вид векторам придал американский физик Дж. Гиббс ( рис . 1 ).
Я учусь в классе естественнонаучного профиля, а значит, буду связывать свои профессии с химией, физикой, биологией. Поэтому, мне предстоит изучать математику и в высших учебных заведениях. Я побеседовала с выпускниками 2003 г. нашей школы, которые учатся в КамГТУ и КамГУ на физико-математическом факультете и факультете «управление и информатика в технических системах». И выяснила, что одним из многих предметов будет «Векторная алгебра», элементы которой я уже изучила в школьном курсе математики и использую в физике в разделе «Механика», «Электричество», химии при составлении реакций, биологии и др.
Направленным отрезком или вектором называется отрезок, для которого указано какая из его граничных точек считается началом, а какая – концом . Направление вектора (от начала к концу) на рисунках отмечается стрелкой ( рис .2 ). Длиной ненулевого вектора называется длина отрезка . В векторной алгебре важную роль играют линейные операции над векторами: операция сложения векторов и умножения вектора на действительное число. Суммой векторов и называют вектор, идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора ( рис. 2 ). Это правило используется нами при сложении сил в физике (векторных величин, рис .3 ).
Применение векторной алгебры тесно связано с различными типами векторных произведений: скалярного, векторного и смешанного. Понятие скалярного произведения векторов применяется, например, в физике, при рассмотрении работы силы F на заданном пути S : работа равна | F || S | cosj, где j — угол между векторами F и S . В механике, физике широко используются понятия векторного поля. Примерами векторных полей могут служить также поле силы тяжести, магнитное и электрическое напряжение электромагнитного поля ( рис .5 ).
Векторы, изучаемые в математике, помогают мне в физике. Физические формулы, законы, чаще всего изображаются математическими знаками, в частности векторами. Любая сила, например F тяжести, раскладывается по векторам. Это необходимо при расчётах в строительстве различных сооружений, например в построении моста, через реку Авача в г. Елизово ( рис .4,6 ). Так неправильные расчёты могут привести к трагедиям и многочисленным жертвам ( рис .7 ). Разложение векторов применяют при расчётах летательных аппаратов, например вектор скорости для круговых орбит ( рис .8 ), в навигации морского и воздушного флота ( рис . 9 ). Планирую вместе с классом в этом учебном году совершить экскурсию в аэропорт в аэронавигационную службу и посмотреть практическое применение векторов при расчётах полётов истребительных самолётов.
Своё широкое применение векторы получили в химии. Например, рассмотрим электронное строение атома азота ( рис .10,11 ). Каждый электрон имеет свою собственную характеристику – спин. Спин – собственный момент импульса электрона, не связанный с движением в пространстве. Спины электронов складываются как вектора. Сумма спинов данного числа электронов на подуровне должна быть максимальной. Если в квантовой ячейке находятся два спаренных электрона, то их изображают противоположно направленными векторами.
Векторная модель атома. Модель основана на рассмотрении векторного сложения угловых моментов электронов в атоме. Силовой угловой момент имеет (2I+1) различных компонентов ( рис.23 ).
Обратимость реакции. Обратимыми называются реакции, протекающие в двух взаимно противоположных направлениях. Такие реакции не доходят до конца и заканчиваются установлением химического равновесия, при котором скорости прямой и обратной реакций равны между собой.
Обратимые реакции не доходят до конца. Концентрации реагентов уменьшаются, что приводит к уменьшению скорости прямой реакции . Скорость же обратной реакции постоянно возрастает, поскольку увеличиваются концентрации продуктов. Когда скорости прямой и обратной реакции станут одинаковыми ( ), наступает состояние химического равновесия. Человек научился направлять обратимые химические реакции в нужную для себя сторону, используя действие таких факторов, как температура, давление, концентрация.
Диссоциация. Диссоциация – распад молекул на ионы. Ассоциация – соединение ионов в молекулу.
Уравнения химических реакций в органической химии. В органической химии уравнения химических реакций записывают, использую вектор между левой частью уравнения и правой. Объяснение этому факту состоит в том, что большинство химических реакций между органическими веществами имеют несколько направлений течения. Могут образовываться различные продукты реакции при взаимодействии одних и тех же веществ, только количественное соотношение продуктов реакций различно, поэтому записывают то уравнение химической реакции, в котором продуктами реакции являются вещества, выход которых больше. Это и будет являться основным уравнением. Чтобы указать на существование побочных процессов, используют знак вектора.
CH 3 CH 2 CH 2 Cl
CH 3 CH CH 2 + HCl
Электролиз. Электролиз — это окислительно-восстановительный процесс, протекающий на электропроводах при прохождении электрического тока через расплав или раствор электролита.
Знаком вектора обозначается осадок, т.е. нерастворимое вещество, которое выпадает на дно сосуда, или газ, который уходит вверх, в атмосферный воздух ( рис .12 ). Для проведения опыта я взяла мелко измельченный мрамор и прилила соляную кислоту, происходит бурная реакция c выделением углекислого газа, описываемая уравнением
CaCO 3 +2HCl=CaCl 2 +CO 2 +H 2 O
Второй опыт я провела, используя раствор сульфата меди и гидроксида натрия, в котором наблюдала выпадение голубого осадка гидроксида меди:
CuSO 4 +2NaOH=Cu(OH) 2 +Na 2 SO 4 ( рис .13 )
Интересно, но понятие «вектор» встречается даже в биологии. И вы будете ещё больше удивлены, когда узнаете, что эти векторы изображены на рисунках ( рис . 14 ). Это вошь, клещ, крыса…
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы, а клещи являются переносчиками вируса, вызывающего энцефалит. Так эти заболевания являются очень опасными для человека, поэтому необходимо досконально изучить механизм их передачи во избежание заражения. Существует ещё одно значение слова «вектор» в биологии. На этот раз немножко коснёмся генной инженерии.
Вектор – это автономная молекула ДНК, используемая в генной инженерии, для переноса генов от организма-донора в организм-реципиент, а также для клонирования нуклеиновых последовательностей ( клонирующий вектор ).
Вектором, например, является бактериальная плазмида. Плазмиды дают бактериям большие преимущества, например способность синтезировать вещества опасные для других бактерий – антибиотики, а так же быть устойчивыми к антибиотикам своих собратьев ( рис.15 ). Эти свойства научился использовать в своей деятельности человек, но они так же могут и вредить ей. Например, был получен антибиотик против бактерии, вызывающей туберкулёз, но эта бактерия эволюционировала и приобрела к нему невосприимчивость. Поэтому необходимо снова искать средство, что бы справиться с этой болезнью. Человек создаёт также искусственные векторы.
С помощью векторов синтезируются различные лекарства и антибиотики. Синтезируются ферменты или даже целые каскады ферментов, необходимые человеку (например, инсулин). В генной инженерии существует такое молодое развивающееся направление, как генотерапия, где векторы позволяют исправлять генетические дефекты. Эти молекулы ДНК (векторы) используются также при создании трансгенных растений и животных (например, генетически модифицированные овцы продуцируют человеческий ген альфа 1-антитрипсина в молоке). Люди, наследующие два нефункционирующих гена этого белка, страдают болезнью, называемой альфа 1-антитрипсиновой недостаточностью. Она поражает легкие и иногда печень. Векторы применяются также при клонировании.
В обычном понимании клоном считается идентичная копия высшего организма. Молекулярные биологи, однако, клоном считают популяцию генетически идентичных организмов, клеток, вирусов или молекул ДНК. В генетической инженерии цель клонирования, как правило, — получение значительного количества копий специфического гена. Первый шаг на этом пути – создание библиотеки, для которого понадобятся векторы. Идеальный вектор для генетической инженерии должен иметь три характеристики:
- Хороший потенциал клонирования. То есть должен давать большое количество реплик в хозяйской клетке.
- Его геном должен иметь один сайт узнавания для каждого из многих ферментов рестрикции. Таким образом, чужой ген сможет встраиваться только в одну точку вектора.
- он должен иметь полезную информацию в клетке, например нести ген устойчивости к антибиотику, чтобы можно было легко отличить клетки, несущие вектор, и выделить встроенный в него ген.
Векторы вокруг нас.
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Я люблю свой город Елизово и часто гуляю по его улицам, хожу в магазины, посещаю театр, выставки, музеи и т. д. Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора ( рис . 16 ). А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время. Но большинство векторов я встречаю на вывесках или баннерах на улицах. На баннере, например, можно увидеть преимущество того или иного банка (% кредита или накопительный) ( рис .17 ). Вывески помогают мне найти местонахождение нужного магазина, службы или другого необходимого объекта ( рис . 18 ).
Векторы в знаках дорожного движения.
Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителей ( рис . 19 ). В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. На примере знаков: 4.1.1 «Движение прямо», 4.1.2 «Движение направо», 4.1.3 «Движение налево», 4.1.4 «Движение прямо и налево» и другие ( рис . 20,21 ). Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог. Не соблюдение этих правил и пренебрежение знаками приводит к необратимым последствиям (автокатастрофам), что, конечно же, не обходится без человеческих жертв, в том числе и детей ( рис . 22 ).
Базовое понятие «вектор», рассмотренное на уроках математики, является основой для дальнейшего изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию (в знаках дорожного движения), и избежать опасных ситуаций на дороге. Призываю всех, серьёзно отнестись к правилам дорожного движения, быть внимательными на дорогах, не проходить мимо детей, нарушающих их, и самим этого не делать.
- Атанасян Л. С., В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 7-9. Издательство «Просвещение», 2007г., 384с.
- Атанасян Л. С., В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 10-11. Издательство «Просвещение», 2007г., 285с.
- Малугин В. А., Математика для экономистов: Линейная алгебра. Курс лекций. Глав 3. Векторная алгебра. Москва; Эксмо, 2006г., 224с.
- Беклемишев Д. В., Курс аналитической геометрии и линейной алгебры. Москва; Наука, 1988г.
- Перышкин А. В., Физика 9 класс: Учебник для общеобразовательных учреждений; М.: «Дрофа», 2004 г. – 256с.
- Мякишев Г. Я., Физика: учебник для 10 класса общеобразовательных учреждений; М.: «Просвещение», 2005г. – 366с.
- Мякишев Г. Я., Физика: учебник для 11 класса общеобразовательных учреждений; М.: «Просвещение», 2004г. – 382с.
- Габриелян О. С., Химия. 11 класс: учебник для общеобразовательных учреждений; М.: «Дрофа», 2005г. – 362[6]с.
- Лидин Р. А., Аликберова Л. Ю., Химия. Справочник для старшеклассников и поступающих в ВУЗы; М.: «АСТ-ПРЕСС ШКОЛА», 2006г. – 512 с.
- Кузьменко Н. Е., Ерёмин В. В., Попков В. А., Начала химии. Современный курс для поступающих в ВУЗы. Т.1; М.: «Экзамен», 2002г. – 384 с.
- Глинка Н. Л., Общая химия: Учебное пособие для вузов; М.: «Интеграл-Пресс», 2008 г. – 728 с.
- Уиллет Э., Генетика без тайн; М.: «Эксмо», 2008г. – 224с.
- Тейлор Д., Грин Н., Стаут У., Биология. Т.3; М.: «МИР», 2006г. – 451с.
- Правила дорожного движения Российской Федерации с иллюстрациями; М.; ООО «АТБЕРГ 98», 2007г.
💡 Видео
Координаты точки и координаты вектора 1.Скачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Координаты вектора.Скачать

Математика это не ИсламСкачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Как найти координаты вектора?Скачать

Координаты вектора. Видеоурок по геометрии 9 классСкачать

КООРДИНАТЫ ВЕКТОРА // 9 класс // геометрияСкачать

§3 Координаты вектораСкачать

КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ решение задачСкачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

90. Координаты вектораСкачать