Вектор тока активной нагрузки

Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.

Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.

Видео:Реактивная мощность за 5 минут простыми словами. Четкий #энерголикбезСкачать

Определение

Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.

Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.

Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.

Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.

Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.

Видео:Векторные диаграммы и коэффициент мощностиСкачать

Разновидности

Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:

1. Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
2. Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.

Векторную диаграмму токов можно построить 2 разными способами:

1. Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.
2. Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Построение

Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.

1. Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
2. Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
3. Напряжение резистора UR 10 вольт, его направление совпадает с током I.
4. Сила тока в цепи I равняется 3 ампера.

Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.

1. Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.
2. Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.
3. Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.
4. Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.
5. Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.

Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.

Видео:Векторная диаграммаСкачать

Способ 2

Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:

• Резистора UR;
• Конденсатора UC;
• Катушки UL.

1. На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.
2. От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.
3. От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.

Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.

1. Показать результат сложения вектора UL и UC.
2. При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.
3. Кроме того можно определить угол сдвига фазы φ в цепи.

Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.

Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:

1. На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
2. Угловая величина обозначается как W.
3. Также присутствует сам вектор Im и угол сдвига фаз φ.

Далее нужно сделать:

1. На плоскости выбрать точку отсчета.
2. От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
3. Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.

Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.

Видео:Коэффициент мощности простыми словамиСкачать

Заключение

Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.

Видео:Коэффициент мощности "косинус фи"Скачать

Видео по теме

Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Формула полной реактивной мощности емкостная и индуктивная. Щелкаем реле правильно: коммутация мощных нагрузок

Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).

Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.

В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии. Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю. Рассмотрим, возможно ли подобное, и насколько можно приблизиться к идеалу.

Активная и реактивная мощность

Активная мощность

Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.

Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность . Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).

Реактивная мощность

Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).

Реактивная емкостная мощность

Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке. Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.

Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т.е. на четверть периода.

Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.

Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.

Реактивная индуктивная мощность

Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.

Видео:Урок 363. Мощность в цепи переменного токаСкачать

Активная нагрузка

К устройствам с активной нагрузкой причисляются нагревательные приборы (утюги, электроплиты, лампы накаливания, электрические чайники). Подобные приборы вырабатывают тепло и свет. Они не содержат индуктивности и емкости. Активная нагрузка преобразовывает электроэнергию в свет и тепло.

Реактивная нагрузка содержит емкость и индуктивность. Данные параметры имеют качество собирать энергию, а потом отдавать ее в сеть. Примером может служить электродвигатель, электрическая мясорубка, бытовой инструмент (пылесос, кухонный комбайн). То есть, все устройства, которые содержат электродвигатели.

Видео:Теоретические основы компенсации реактивной мощностиСкачать

Треугольник мощностей

Чтобы разобраться с реактивной нагрузкой рассмотрим треугольник мощностей.

где Р – активная мощность, которая измеряется в Ватах и используется для совершения полезной работы;

Q – реактивная, которая измеряется в Варах и используется для создания электромагнитного поля;

S – полная мощность используется для расчета электрических цепей.

Для расчета полной мощности применяем теорему Пифагора: S 2 =P 2 +Q 2 . Или с помощью формулы: S=U*I, где U – это показание напряжения на нагрузке, I — показание амперметра, которое включается последовательно с нагрузкой. В расчетах также используется коэффициент мощности – cosφ. На приборах, которые относятся к реактивной нагрузке, обычно указаны активная мощность и cosφ. С помощью этих параметров также можно получить полную мощность.

Иногда на приборах указывается полная мощность, а cosφ не указан. В этом случае применяется коэффициент 0,7.

Видео:Урок 1.6: Активная и реактивные нагрузкиСкачать

Активно-емкостная нагрузка

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Рисунок 11 – Схема с активно-емкостной нагрузкой

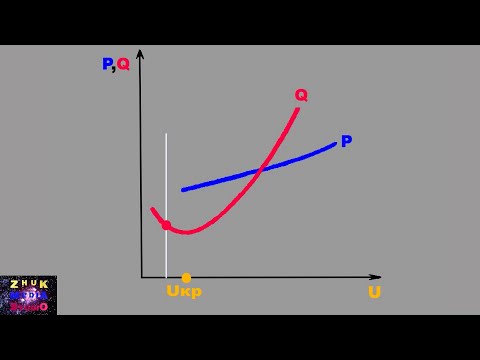
Рассмотрим влияние активно-емкостной нагрузки на примере работы однофазного мостового выпрямителя.

Рисунок 12 – Зависимость токов и напряжений

На рисунке представлены графические зависимости токов и напряжений, поясняющие переходные процессы в схеме в момент подключения выпрямителя к источнику U1.

На интервале tзар U1>UС и при этом происходит заряд емкости C сглаживающего фильтра через внутреннее сопротивление выпрямительного звена. При этом появляется большой импульсный ток, значения которого в 20…40 раз выше установившегося значения средневыпрямленного тока вентиля. Особенно это выражено в источниках питания с бестрансформаторным входом. Для ограничения этого тока вводят резисторы, терморезисторы или резисторы шунтированные управляемыми ключами, выполненные на симисторах, тиристорах или динисторах. Ключи позволяют с учетом времени установления переходного процесса производить ограничение тока только в момент пуска источника питания, следовательно, повышаются КПД и надежность выпрямителя.

На интервале tраз, когда напряжение на емкости уравнивается с напряжением источника, конденсатор разряжается на нагрузку. С увеличением тока нагрузки увеличивается уровень пульсации выпрямленного напряжения из- за уменьшения постоянной цепи разряда tраз =RНС. При этом ухудшаются сглаживающие действия фильтра.

При расчете выпрямителя с емкостной нагрузкой используют метод Терентьева – метод номограмм. Он основан на расчете вспомогательных коэффициентов зависящих от угла протекания тока через вентиль. Вводят коэффициент А=f(q), где q — угол протекания тока через вентиль. Для различных схем выпрямителей приводятся номограммы, которые получены экспериментальным путем для различных мощностей и схем выпрямителей. Расчет параметров Uобр, Iаср, Iад, U2, I2 выполняют через вспомогательные коэффициенты: В, С, D=f(A). Для получения связи среднего тока через вентиль с параметром А проведем интегрирование на интервале q. При выводе соотношения примем емкость конденсатора, близкую к бесконечности (СÞ¥ ), а пороговое напряжение диода равным нулю. Для получения среднего значения тока через вентиль переместим оси координат в середину импульса тока и воспользуемся уравнением для среднего значения тока: (1)

Нижеприведенные диаграммы поясняют вывод соотношений для Ud.

Рисунок 13 – Диаграммы соотношений для Ud

На интервале 2q ток вентиля совпадает с током нагрузки. Приравняем (1) и (2) и поделим внутреннюю скобку в выражении (1) на cosq, получим: .

Схема удвоения напряжения

Классическая (симметричная) схема удвоения состоит из двух однотактных выпрямителей, каждый из которых использует свою полуволну напряжения.

Рисунок 14 – Схема удвоение напряжения

Рисунок 15 – График напряжения

Напряжение на нагрузке складывается из напряжений на конденсаторах С1 и С2. Если пульсации малы, то постоянная составляющая на каждом конденсаторе U01 ≈ U2m , а напряжение на нагрузке U0 ≈ 2U2m . Кроме того, при сложении компенсируется первая и все нечетные гармоники пульсаций. Поэтому схема ведет себя как двухтактная, хотя и состоит из двух однотактных схем. Недостатком симметричной схемы удвоения, с точки зрения безопасности, является отсутствие общей точки нагрузки и трансформатора.

Используется также и несимметричная схема удвоения, её отличием от предыдущей является то, что нагрузка имеет общую точку с трансформатором. Поэтому их можно соединить с корпусом, при этом основная частота пульсаций равна частоте сети.

Рисунок 16 – Несимметричная схема удвоения напряжения

Рисунок 17 – График напряжения несимметричной схемы

В этой несимметричной схеме конденсатор С1 выполняет функцию промежуточного накопителя, не участвует в сглаживании пульсаций, поэтому её массогабаритные показатели хуже, чем у симметричного удвоителя. Однако есть и достоинства. Схему можно изобразить так:

Рисунок 18 – Альтернативная несимметричная схема

Получилась регулярная структура, которую можно наращивать и получить умножитель напряжения.

Рисунок 19 – Множитель напряжения

Нагрузку можно подключить к любой группе конденсаторов и получить чётное или нечётное умножение. На схеме показано чётное умножение — напряжение на нагрузке U0 ≈ 6Um2 . Обычно такие умножители собирают в виде единого блока и заливают компаундом. Число конденсаторов в схеме равно коэффициенту умножения.

Расчетные соотношения для рассмотренных схем можно найти в справочнике. Недостатком схем умножения является их высокое внутреннее сопротивление и низкий коэффициент полезного действия вследствие большого числа перезарядов.

Более высоким КПД обладают бестрансформаторные высоковольтные выпрямители с одновременным зарядом n штук накопительных конденсаторов С1.

Рисунок 20 – Бестрансформаторный высоковольтный выпрямитель

Управляемые зарядный и разрядные ключи Кз и Кр работают синхронно и в противофазе. конденсаторы С1 параллельно заряжаются от сети и последовательно разряжаются на нагрузку через разрядные ключи Кр. При этом, напряжение на нагрузке в n раз больше амплитуды напряжения сети.

Лекция 4. Управляемые выпрямители.

Режимы работы выпрямителей

В зависимости от вида выпрямленного тока существует три режима. Обозначим угол проводимости вентилей– λ.

Режим работы, при котором токи вентилей следуют друг за другом без пауз, но выпрямленный ток спадает до нуля, называется граничным (рис. 5.1 а). В граничном режиме угол проводимости вентилей mπ = λ 2 гр. (5.1)

Режим работы, при котором токи вентилей следуют друг за другом с паузой, называется прерывистым (рис. 5.1 б). В прерывистом режиме угол проводимости вентилей mπ

В остальное время энергию из сети конденсатор не потребляет. В этом случае ток имеет импульсное качество. К чему это все приводит? Это приводит к тому, что синусоида искажается. Но не все электронные устройства работают с искаженной синусоидой. Эта проблема решается за счет применения стабилизаторов двойного преобразования, где сетевое питание преобразуется в постоянное. Затем из постоянного преобразуется в переменное нужной формы и амплитуды.

Видео:Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Пусковой ток

При расчете необходимо учитывать и пусковые токи устройства. Например, сопротивление нити накаливания в лампочке в момент включения в 10 раз меньше, чем в рабочем режиме. Следовательно, пусковой ток этой лампочки в 10 раз больше. Через некоторое время она начнет потреблять ту мощность, которая записана в данных этой лампочки. Поэтому, при включении она перегорает за счет больших пусковых токов.

В радиоэлектронной аппаратуре пока не зарядится конденсатор в блоке питания, также образуется пусковой ток.

В электродвигателях тоже образуется пусковой ток, пока двигатель не наберет номинальные обороты.

В нагревательных приборах пусковой ток образуется, пока спираль не нагреется до дежурной температуры.

Видео:лекция 408 Коэффициент мощности в цепи синусоидального токаСкачать

Смысл реактивной нагрузки

В электрической цепи с реактивной нагрузки фаза тока и фаза напряжения не совпадают во времени. В зависимости от характера подключенного оборудования напряжение либо опережает ток (в индуктивности), либо отстаёт от него (в ёмкости). Для описания вопросов используют векторные диаграммы. Здесь одинаковое направление вектора напряжения и тока указывает на совпадение фаз. А если вектора изображены под некоторым углом, то это и есть опережение или отставание фазы соответствующего вектора (напряжения или тока). Давайте рассмотрим каждый из них.

В индуктивности напряжение всегда опережает ток. «Расстояние» между фазами измеряется в градусах, что наглядно иллюстрируется на векторных диаграммах. Угол между векторами обозначается греческой буквой «Фи».

В идеализированной индуктивности угол сдвига фаз равен 90 градусов. Но в реальности это определяется полной нагрузкой в цепи, а в реальности не обходится без резистивной (активной) составляющей и паразитной (в этом случае) емкостной.

В ёмкости ситуация противоположна – ток опережает напряжение, потому что индуктивность заряжаясь потребляет большой ток, который уменьшается по мере заряда. Хотя чаще говорят, что напряжение отстаёт от тока.

Если сказать кратко и понятно, то эти сдвиги можно объяснить законами коммутации, согласно которым в ёмкости напряжение не может изменится мгновенно, а в индуктивности – ток.

Видео:3,5 Режим нагрузки трансформатораСкачать

Виды энергии

Ниже представлены основные виды нагрузок, которые используются в повседневной жизни. Они могут быть как в бытовых приборах, как и в различных двигателях или датчиках.

Активная

Для данной работы используется закон Ома, который выполняется в каждую секунду времени и схож с правилом для переменного тока. Такой тип применяется в лампах для освещения или в электроплитах.

Вам это будет интересно Применение полевых транзисторов

Активно емкостная нагрузка формула

Емкостная

Этот вид превращает в течении определенного времени энергию электрического тока в электрополе, а далее превращает ее в электрический ток. А также, здесь сила тока будет опережать напряжение.

В качестве примера может быть конденсатор. К сожалению, встретить полные реактивные нагрузки невозможно ни в одном приборе. Каждый вид не имеет коэффициент полезного действия 100%, потому что существуют потери энергии в воздухе и прочее. Потому чаще всего используется название активно-реактивной работы.

Индуктивная

Данный вид превращает энергию в магнитное поле, а далее меняет ее в электрический ток. Сила тока в этом случае будет отставать от напряжения. Для примера можно взять индуктивную катушку или датчик дросселя на автомобиле.

Функционирование выпрямителей

Видео:компенсация реактивной мощности в бытуСкачать

Треугольник мощностей и косинус Фи

Если взять всю цепь, проанализировать её состав, фазы токов и напряжений, затем построить векторную диаграмму. После этого изобразить активную по горизонтальной оси, а реактивную – по вертикальной и соединить результирующим вектором концы этих векторов – получится треугольник мощностей.

Он выражает отношение активной и реактивной мощности, а вектор, соединяющий концы двух предыдущих векторов – будет выражать полную мощность. Всё это звучит слишком сухо и запутано, поэтому посмотрите на рисунок ниже:

Буквой P – обозначена активная мощность, Q – реактивная, S – полная.

Формула полной мощности имеет вид:

Самые внимательные читатели наверняка заметили подобие формулы теореме Пифагора.

• P – Вт, кВт (Ватты);
• Q – ВАр, кВАр (Вольт-амперы реактивные);
• S – ВА (Вольт-амперы);

Видео:Реактивная мощность и напряжениеСкачать

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

Реактивная нагрузка бывает двух видов:

1. Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
2. Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Емкостная и индуктивная нагрузка

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Видео:Компенсация реактивной мощности. Практика. Расчет емкости.Скачать

Расчёты

Для вычисления полной мощности используют формулу в комплексной форме. Например, для генератора расчет имеет вид:

А для потребителя:

Но применим знания на практике и разберемся как рассчитать потребляемую мощность. Как известно мы, обычные потребители, оплачиваем только за потребление активной составляющей электроэнергии:

P=S*cosФ

Здесь мы видим, новую величину cosФ. Это коэффициент мощности, где Ф – это угол между активной и полной составляющей из треугольника. Тогда:

cosФ=P/S

В свою очередь реактивная мощность рассчитывается по формуле:

Q = U*I*sinФ

Для закрепления информации, ознакомьтесь с видео лекцией:

Всё вышесказанное справедливо и для трёхфазной цепи, отличаться будут только формулы.

Видео:Электричество за 2 минуты! Напряжение, сила, мощность, постоянный и переменный ток. ПРОСТО О СЛОЖНОМСкачать

Косинус фи

На графике видно, что угол φ образуют два вектора, полной и активной мощности. Чем их величины меньше отличаются, тем лучше, но полному их слиянию мешает реактивная мощность, считающаяся паразитной. Чем больше угол, тем выше нагрузка на линии электропередач, повышающие и понижающие трансформаторы системы энергоснабжения, и наоборот, чем ближе вектора наклонены друг к другу, тем меньше будут греться провода на всем протяжении цепи. Естественно, что с этой проблемой что-то нужно было делать. И решение нашлось, простое и изящное. Взаимная компенсация реактивной мощности позволяет уменьшить угол φ и максимально приблизить его косинус (который также называют коэффициентом мощности) к единице. Для этого следует удлинить вектор емкостной составляющей так, чтобы добиться резонанса токов, при котором они «погасят» друг друга (в идеале полностью, а на практике — наибольшим образом).

Видео:Векторная диаграмма токов и топографическая диаграмма напряженийСкачать

Работа трансформатора под нагрузкой и векторные диаграммы

Работа трансформатора зависит от типа нагрузки на вторичной обмотке трансформатора. Нагрузка может быть двух видов: активно-индуктивная и активно-емкостная. Теоретически может быть чисто активная. В зависимости от нагрузки вектор тока I₂’ может отставать от ЭДС E₂’ на угол ф₂, который называется вторичным углом нагрузки.

Если нагрузка активно-емкостная, то I₂’ опережает ЭДС E₂’ на угол нагрузки ф₂.

Для того чтобы определить ток, проводим вектор, параллельный вектору I₂’ и равный ему по величине. Соединяем конец вектора I₂’ с началом координат. Так как в режиме нагрузки ток протекает по первичным и вторичным обмоткам трансформатора, напряжение будет отличаться от ЭДС.

Строим векторы напряжения. Сначала U₁. Для этого из конца вектора E1проводим вектор, параллельный вектору тока I₁ и равный r₁I₁. Из конца этого вектора r₁I₁ перпендикулярно проводим jx₁I₁.

Векторная диаграмма трансформатора при смешанной активно-индуктивной нагрузке.

Векторная диаграмма трансформатора при смешанной активно-ёмкостной нагрузке.

Из векторной диаграммы видно, что напряжение U₁ не зависит от типа нагрузки и всегда опережает ЭДС E₁.

Напряжение U₂ всегда отстает от ЭДС E₂’ и не зависит от типа нагрузки, зато от типа нагрузки зависят угол опережения напряжения U₁ и угол отставания напряжения U₂.

Угол между током I₁ и ЭДС E₁ обозначается ф₁ и называется первичным углом нагрузки.

Ток I₂’ – ток нагрузки – зависит от величины активной и реактивной составляющих.

Если изменить активную составляющую тока нагрузки I₂’, изменяется и по длине и по амплитуде ф₁. При изменении реактивной составляющей тока I₂’ изменяется угол ф₂, а длина вектора остается прежней.

Упрощенная векторная диаграмма трансформатора при смешанной активно-индуктивной нагрузке.

🎦 Видео

Мощность в цепи переменного тока. 11 класс.Скачать

Анализ векторной диаграммы. Часть 2Скачать