Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Онлайн калькулятор

радиус r =
угол α =
Видео:Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать

Теория
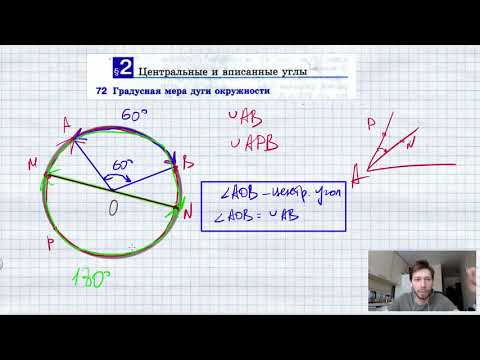
Чему равна длина дуги окружности L если её радиус r, а угол между двумя прямыми, проведёнными от центра окружности к конечным точкам дуги — центральный угол α?
Формула
Если угол в градусах:
Если угол в радианах:
Пример
Для примера посчитаем чему равна длина дуги окружности с радиусом r = 2 см и центральным углом α = 45° :
L = 3.14 ⋅ 2 ⋅ 45/180 = 6.28 ⋅ 0.25 = 1.57 см
Видео:Градусная мера дуги окружности | Геометрия 7-9 класс #70 | ИнфоурокСкачать

Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Видео:72. Градусная мера дуги окружностиСкачать
Окружность и круг. Онлайн калькулятор
С помощю этого онлайн калькулятора окружности можно найти радиус, диаметр, площадь окружности и т.д. по известным элементам. Для нахождения элементов окружности выберите требуемый элемент для вычисления, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

1. Определение окружности
Определение 1. Окружность − это геометрическая фигура состоящая из всех точек плоскости равноудаленных от данной точки O (Рис.1).
 |
Точка O называется центром окружности. Отрезок, соединяющий центр окружности с какой-либо точкой окружности, называется радиусом окружности. Длина этого отрезка также называют радиусом окружности. Из определения 1 следует, что все радиусы окружности имеют одну и ту же длину.
Видео:Радианная мера угла. 9 класс.Скачать

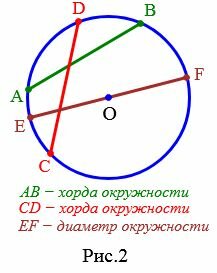
2. Хорда
Отрезок, соединяющий две точки окружности, называется хордой (Рис.2). Хорда, проходящая через центр окружности, называется диаметром.
 |
Видео:Длина дуги окружности. 9 класс.Скачать

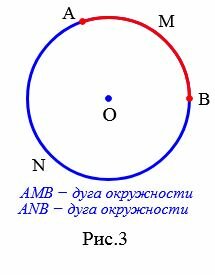
3. Дуга окружности
Отметим на окружности любые две точки A и B. Эти точки делят окружность на две части. Каждая из которых называется дугой окружности (Рис.3). Чтобы различать эти дуги, на каждой из них отмечают промежуточную точку. Например M и N (Рис.3). Обозначают эти дуги так: ◡AMB и ◡ANB. Иногда в обозначении промежуточную точку пропускают, если известно о какой дуге идет речь.
 |
Видео:Градусная мера угла. 9 класс.Скачать

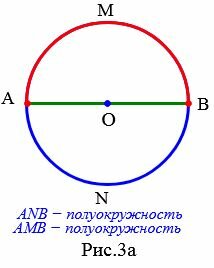
4. Полуокружность
Дуга называется полуокружностью, если отрезок, соединяющий ее концы является диаметром окружности. На рисунке 3a изображены две полуокружности: AMB и ANB.
 |
Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

5. Определение круга
Определение 2. Круг − это геометрическая фигура состоящая из всех точек плоскости удаленных от данной точки O на рассояние не больше заданного неотрицательного числа R (Рис.4).
 |
O − называется центром круга. R− радиус круга. Из определения 2 следует, что окружность является частью круга. Такой круг называется замкнутым.
Представим другое определение круга.
Определение 3. Круг − это геометрическая фигура состоящая из всех точек плоскости удаленных от данной точки O на рассояние меньше заданного неотрицательного числа R (Рис.5).
 |
В этом определении окружность не входит в круг. Такой круг называется открытым.
Еще одно определение круга.
Определение 4. Круг − это часть плоскости, которая лежит внутри окружности.
Обычно под понятием круг понимают замкнутый круг. Если имеется в виду открытый круг, то надо об этом объявить.
Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

6. Сектор круга
Определение 5. Часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга называется сектором круга.
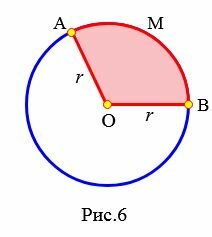 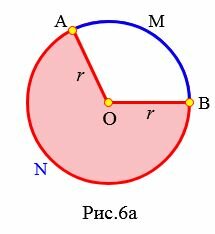 |
На рисунке 6 окрашенная поверхность − это сектор окружности с центром O. Он находится между дугой AMB и двумя радиусами OA и OB. На рисунке 6a окрашенная поверхность − это сектор окружности с центром O. Он находится между дугой ANB и двумя радиусами OA и OB.
Видео:Математика, 8 класс: Центральный угол. Градусная мера дуги окружностиСкачать

7. Сегмент круга
Определение 6. Часть круга, ограниченная дугой и ее хордой называется сегментом круга.
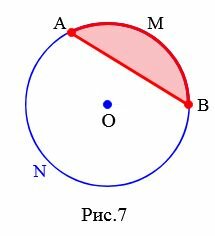 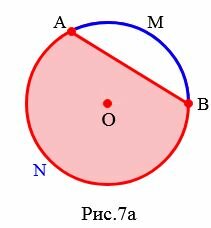 |
На рисунке 7 окрашенная поверхность − это сегмент окружности с центром O. Он находится между дугой AMB и ее хордой AB. На рисунке 7a окрашенная поверхность − это сегмент окружности с центром O. Он находится между дугой ANB и ее хордой AB.
Видео:Математика. 8 класс. Центральный угол. Градусная мера дуги окружности.Скачать

8. Полукруг
Определение 7. Сегмент круга, хордой которого является диаметр этого круга называется полукругом.
 |
На рисунке 8 окрашенная поверхность − это полукруг. Он находится между дугой AMB и ее хордой AB, которая является диаметром данной окружности.
📹 Видео
Длина окружности. Площадь круга - математика 6 классСкачать

Что такое радиан?Скачать

8 КЛАСС | ГЕОМЕТРИЯ | Градусная мера дуги окружностиСкачать

29. Градусная мера дуги окружностиСкачать

Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Длина дуги окружности. Практическая часть. 9 класс.Скачать
ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Градусы. Перевод значения угла в градусах, минутах и секундах в десятичное значение и наоборотСкачать
