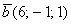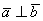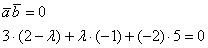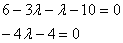Как выяснить ортогональны ли векторы

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

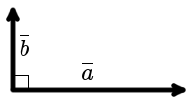рис. 1

Видео:Ортогональность. ТемаСкачать

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = < a_x ; a_y > и b = < b_x ; b_y > , условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 — 8 = 2 n — 4
2 n — 4 = 0
2 n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:2 42 Ортогональность векторовСкачать

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Видео:ОртогональностьСкачать

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Видео:§48 Ортонормированный базис евклидова пространстваСкачать

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = и b ¯ = записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = и b ¯ = ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = и b ¯ = ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2

Ответ: векторы являются ортогональными при значении n = 2 .

Видео:A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = и b ¯ = условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = и b ¯ = являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

1.6.7. Как проверить векторы на ортогональность?

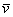
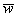
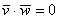
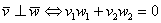
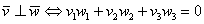
Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю, что векторы и ортогональны тогда и только тогда, когда . В координатах данный факт запишется следующим образом:
(для векторов плоскости);
(для векторов пространства).

Задача 24

а) Проверить ортогональность векторов: 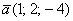и

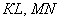
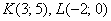
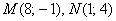
б) Выяснить, будут ли перпендикулярными отрезки , если , .

Решение:

а) Выясним, будут ли ортогональны пространственные векторы. Для этого вычислим их скалярное произведение: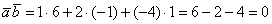
, следовательно,

б) Здесь речь идёт об обычных отрезках плоскости. Отрезки обычные, а задача всё равно решается через векторы. Найдём векторы: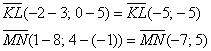

и вычислим их скалярное произведение: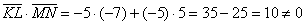
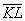
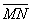
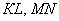
, следовательно, векторы и не перпендикулярны, а значит, не перпендикулярны и отрезки .

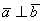
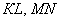
Ответ: а) , б) отрезки не перпендикулярны.

Задача 25

Даны 4 точки пространства и . Выяснить будут ли перпендикулярными следующие прямые:
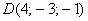
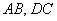
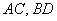
а) , б) .

Это задача для самостоятельного решения. По условию требуется проверить перпендикулярность прямых, а решаем снова через векторы – по полной аналогии с предыдущим примером. Геометрически тоже всё очевидно: из ортогональности векторов автоматически следует перпендикулярность соответствующих прямых. Четыре вектора, которые вы найдёте, называют направляющими векторами прямых.

Мощь аналитической геометрии – в векторах

Так, в рассмотренных задачах, с помощью скалярного произведения можно установить не только ортогональность векторов самих по себе, но и перпендикулярность отрезков, прямых. И это приоткрылась только малая часть красоты предмета.

Завершая разговор об ортогональности, разберу ещё одну небольшую задачку, которая время от времени встречается на практике:

Задача 26

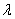
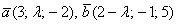
При каком значении векторы будут ортогональны?

Решение: по условию требуется найти такое значение параметра , чтобы данные векторы были ортогональны. Два вектора пространства ортогональны тогда и только тогда, когда .

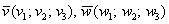
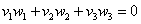
Дело за малым, составим уравнение:

Раскрываем скобки и приводим подобные слагаемые:

Решаем простейшее линейное уравнение:

Ответ: при

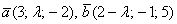
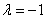
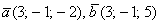
Здесь легко выполнить проверку, в исходные векторы подставляем полученное значение параметра :

и находим скалярное произведение:
– да, действительно, при векторы ортогональны, что и требовалось проверить.

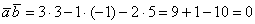
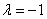
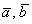
Простенький пример для самостоятельного решения:

Задача 27

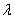
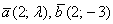
При каком значении скалярное произведение векторов будет равно –2?
Едем дальше:

💥 Видео

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Ортогональные системы векторов. Процесс ортогонализации (задача 1357)Скачать

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Процесс ортогонализации Грама-Шмидта. ПримерСкачать

Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Коллинеарность векторовСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Алгебра и геометрия 12. Ортогональные системы векторов в пространствах со скалярным произведениемСкачать

Ортогональное дополнение (задача 1366)Скачать

Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 11.5. Док-во ортогональности векторовСкачать

Ортогональное дополнение. ТемаСкачать

✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать