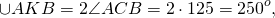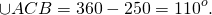Как решать задачи с углом вписанным в окружность (3 видео)

Центральные и вписанные углы

О чем эта статья:

Содержание

Центральный угол и вписанный угол
Свойства центральных и вписанных углов
Примеры решения задач
Вписанные, центральные углы
Свойства вписанных углов
Задачи на окружность с вписанным углом
Задачи на окружность с вписанным углом
Задачи на вписанные углы
Вписанные, центральные углы
Свойства вписанных углов
📺 Видео

Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Видео:Геометрия 8 класс : Решение задач на центральные и вписанные углыСкачать

Вписанные, центральные углы

Вписанный угол – угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.

Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается .

Свойства вписанных углов

Чтобы не потерять страничку, вы можете сохранить ее у себя:

В задаче 11 заметила опечатку Центральным углом для вписанного угла АВС является угол АОС. Будем искать его градусную меру, после чего лишь придется умножить результат на 2, — получим градусную меру угла АВС. Наверное, надо не умножить . а разделить. И хотела поблагодарить Вас за такой сайт. Вы просто молодец. всё очень понятно и доступно.

в задаче 11 на картинке угол АВС равен 106 , а в условии 104 .

Арина, спасибо! Исправлено.

В свойствах вписанных углов небольшая синтаксическая ошибка.
“Угол, опирающийся на диаметр – прямой”. (перед тире запятая не ставится).

Почему в 7-ой задаче angle ADC=120^, так как является смежным с angle BDA. При этом angle BDA=60^, так как опирается на дугу ВА. Тогда разве угол ADC не должен быть равен 60 градусам?

Как же угол ADC будет равен 60°, если он смежен с углом в 60°?

Благодарю вас за такой сайт,очень мне помог, и сделайте пожайлуста ещё одну задачу :Вписанный угол ABC=58гр.Найти хорду на которую опирается этот угол(заранее спасибо)

Даниил, с условием не все в порядке. Не хватает данных. Или радиус должен быть известен или еще что…

В шестой задаче угол BAD разве не будет равен 65? Угол B прямой те опирается на диаметр
Д – 25
180 – 115= 65
Можно ли так?

Угол B не прямой, он не опирается на диаметр!

Видео:Решение задач на тему центральные и вписанные углы.Скачать

Задачи на окружность с вписанным углом

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Задачи на окружность с вписанным углом

Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32°.

Вписанный угол равен половине центрального угла, опирающегося на ту же хорду.

Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Рассмотрим треугольник AOB. Он равносторонний, так как AO = OB = AB = R. Поэтому угол AOB = 60. Вписанный угол ACB равен половине дуги, на которую он опирается. Тем самым, он равен 30°.

Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Вписанный угол дополняет половину центрального угла, опирающегося на ту же хорду, до 180°. Треугольник AOB является равносторонним, т. к. AO = OB = AB = R, поэтому угол AOB = 60°. Тогда

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Задачи на вписанные углы

Рассмотрим некоторые задачи на вписанные углы.

1) По данным рисунка 1 найти угол AOB,

Дуги ACB и AKB дополняют друг друга до окружности. Следовательно, сумма их градусных мер равна 360º.

∠ACB — вписанный угол, опирающийся на дугу AKB.

Значит, градусная мера дуги равна

AOB — центральный угол, опирающийся на дугу ACB, поэтому его градусная мера равна градусной меры этой дуги, то есть, ∠AOB=110º.

2) Точки C и D окружности лежат по одну сторону от диаметра AB.

Найти угол ABD, если ∠BCD=34º.

Соединим точки A и D.

Рассмотрим треугольник ABD.

Так как сумма острых углов прямоугольного треугольника равна 90º, то ∠ABD=90º-∠BAD=90º-34º=56º.

2) В окружности с центром O проведены диаметры AF и BC. Точки C и K окружности лежат по одну сторону от диаметра AF.

Найти угол BCK, если ∠ABC=62º, ∠AFK=20º.

1) Проведем отрезки KC и AC.

2) Рассмотрим треугольник ABC.

∠BAC=90º (как вписанный угол, опирающийся на диаметр).

Поскольку сумма острых углом прямоугольного треугольника равна 90º, ∠ACB=90º-∠ABC=90º-62º=28º.

3) ∠ACK=∠AEK=20º (как вписанные углы, опирающиеся на одну дугу).

Как правило, решение задач на вписанные в окружность углы можно выполнить несколькими способами. Мы рассмотрели только один вариант в каждом случае, но могут быть и другие.

Решение задач на вписанные в окружность треугольники и четырехугольники во многих случаях также сводится к рассмотрению вписанных и центральных углов (или дуг).

Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать