Свертка вектора и тензора (3 видео) | Курс школьной геометрии

Свертка вектора и тензора

Суммой двух тензоров одинакового типа называется тензор, компоненты которого равны суммам соответствующих компонент слагаемых:

То, что сумма тензоров действительно является тензором, ясно из формулы преобразования компонент при замене базиса.

Произведением числа а на тензор называется тензор, полученный из исходного умножением всех компонент на а:

Из этих определений ясно, что тензоры одинакового типа составляют векторнре пространство, размерность которого равна степени с показателем, равным полной валентности.

Содержание

2. Умножение тензоров.
3. Свертка.
Магия тензорной алгебры: Часть 5 — Действия над тензорами и некоторые другие теоретические вопросы
Введение
1. Четыре основных действия над тензорами
1.1. Умножение тензора на скаляр и сложение тензоров (линейная комбинация)
1.2. Умножение тензоров
1.3. Перестановка индексов тензора
1.4. Свертка
2. Симметричные и антисимметричные тензоры
3. Сопутствующий вектор тензора второго ранга
Заключение
Свертка вектора и тензора
📹 Видео

2. Умножение тензоров.

Произведением тензоров и называется система чисел в предположении, что все индексы независимо принимают допустимые значения. Легко видеть, что произведение тензоров есть тензор. Действительно, при замене базиса компоненты преобразуются по формуле

т. e. по формуле изменения компонент тензора пятикратно ковариантного и трехкратно контравариантного. При умножении тензоров их валентности складываются.

Аналогично определяется произведение любого числа тензоров.

Тензор называется разложимым, если его можно представить в виде произведения тензоров валентности 1.

Предложение 1. Любой тензор можно представить в виде линейной комбинации разложимых тензоров.

Доказательство. Зафиксируем базис пространства и рассмотрим векторы t и ковекторы составляющие дуальный базис. Их координаты равны нулю, кроме одной, равной единице. Тензор, равный произведению тензоров из координат этих векторов и ковекторов, имеет единственную компоненту, равную 1, и остальные нули, причем 1 можно получить в любом месте тензора. Следовательно, любой тензор является их линейной комбинацией.

Наименьшее число разложимых тензоров, линейной комбинацией которых является данный тензор, называется его рангом. Легко видеть, что тензор полной валентности 2 имеет ранг, равный рангу соответствующей матрицы. Вопрос об определении ранга полной валентности 3 и выше еще не получил алгорифмического решения в общем виде, и возможно, что даже вопрос о существовании алгорифма не является бесспорным.

3. Свертка.

Пусть имеется тензор имеющий как верхние, так и нижние индексы. Приравнивая один верхний индекс к одному нижнему, мы должны, по соглашению об обозначениях, просуммировать по этому индексу, и в результате получится система элементов, в верхних и нижних номерах которых останется на одну единицу меньше, так что можно положить . Эта операция называется сверткой тензора.

Предложение 2. Свертка произведения тензора на символ Кронекера, как по верхнему, так и по нижнему индексу этого символа, не меняет тензор по существу и сводится только к переименованию индекса.

Действительно, сумма имеет лишь одно слагаемое, отличное от нуля, именно то, для которого значение символа Кронекера равно 1, т. е. при . Поэтому . Аналогично, .

Предложение 3. Результатом свертки тензора является тензор.

Доказательство. Пусть дан тензор . Обозначим через Пусть замена базиса. Тогда компоненты тензора преобразуются по формуле

Переход к требует положить и просуммировать по v. Это дает

Но сумма сравна и сумма и k равна сумме Итак,

Это значит, что b действительно есть тензор.

Видео:ТЕНЗОРЫ ДЛЯ САМЫХ МАЛЕНЬКИХ ЧАЙНИКОВ (ДЛЯ ФИЗИКОВ)Скачать

Магия тензорной алгебры: Часть 5 — Действия над тензорами и некоторые другие теоретические вопросы

Видео:Тензоры 00. Eigenchris. Определение тензоров.Скачать

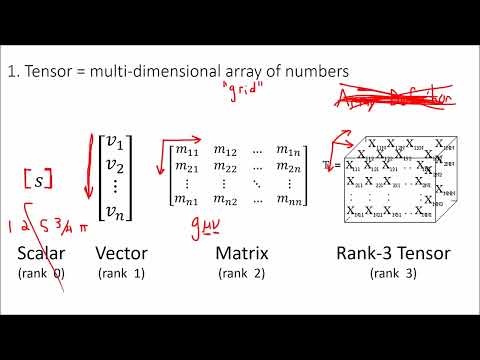
Введение

Прежде чем продолжать рассказ о прикладных аспектах применения тензорного исчисления, совершенно необходимо затронуть ещё тему, обозначенную заголовком. Эти вопросы всплывали в неявной форме во всех предыдущих частях частях цикла. Однако, мной были допущены некоторые неточности, в частности тензорные формы записи скалярного и векторного произведения в статьях 1 и 2 были названы мною «сверткой», хотя на деле они являются комбинацией свертки и умножения тензоров. О сложении, умножение тензоров на число, о тензорном произведении упоминалось только вскользь. О симметричных, антисимметричных тензорах вообще речи не шло.

В этой заметке мы поговорим о тензорных операциях более подробно. Для дальнейших упражнений нам потребуется хорошо в них ориентироваться.

Кроме того, важным является представление о симметричных и антисимметричных тензорах. Мы узнаем о том, что любой тензор можно разложить на симметричную и антисимметричную части, а также познакомимся с тем фактом, что антисимметричной части тензора можно поставить в соответствие псевдовектор. Многие физические величины (к примеру угловая скорость) являются псевдовекторами. И именно тензорный подход к описанию физических явлений позволяет выявить истинную природу некоторых величин.

Видео:Алгебра и геометрия 41. Свертка тензоров. Тензорная алгебра пространства. Симметричная алгебраСкачать

1. Четыре основных действия над тензорами

Видео:МСС лекция 4 семестр 2 часть 1 - Тензоры от чайника к чайникамСкачать

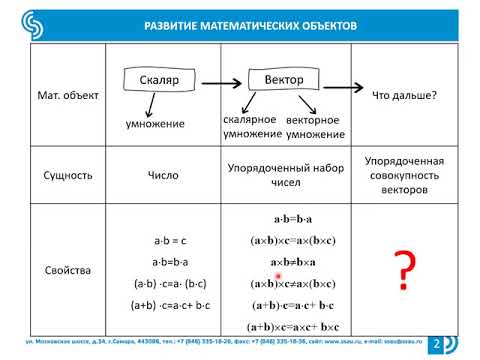
1.1. Умножение тензора на скаляр и сложение тензоров (линейная комбинация)

Под умножением на число понимают умножение на это число каждой компоненты исходного тензора. В результате получается тензор того же ранга, что и исходный.

Складывать же, можно только тензоры, имеющие одинаковый ранг. В бескомпонентной записи линейная комбинация тензоров выглядит так

где — скаляры. Если перейти к компонентной записи, то, например, для тензоров второго ранга данная операция выглядит следующим образом

Видео:Относительность 12 - ТензорыСкачать

1.2. Умножение тензоров

Умножение выполняется над тензорами любого ранга. Результатом является тензор суммарного ранга. Пусть, например — тензор ранга (0,1), а — тензор ранга (0,2). Тогда результатом их умножения будет тензор ранга (0,3)

или, в компонентной форме

С тензорным произведением мы уже сталкивались во второй статье, рассматривая диаду. Вернемся к этому ещё раз, перемножив два вектора

что в компонентной форме

дает матричное представление полученной диады

Из последних примеров, в частности видно, что в общем случае тензорное произведение не коммутативно

что очень легко проверить, выписав умножение в компонентной форме и выписав матричное представление диады

Очевидно, что , но так же очевидно и то, что

Это является следствием выполнения другого действия над тензорами

Видео:Жесткая математика. Пространство. Вектор и пространство векторов. Метрический тензор - это просто!Скачать

1.3. Перестановка индексов тензора

При этом из компонент исходного тензора образуется новая совокупность величин, с другим порядком индексов. Ранг тензора при этом не изменяется. Например, из тензора ранга (0,3) можно получить три других тензора , и , таких что

Для тензоров второго ранга возможно лишь одна перестановка, называемая транспонированием

Выше, когда мы рассмотрели не коммутативность тензорного произведения и переставили векторы, образующие диаду мы как раз и выполнили перестановку индексов, ведь перестановка множителей ведет к перестановке индексов результирующего тензора

Видео:Лекция 53. Свёртка тензоров, спуск индексаСкачать

1.4. Свертка

Сверткой называется суммирование компонент тензора по какой-либо паре индексов. Это действие выполняется над одним тензором и на выходе дает тензор с меньшим на два. Скажем, для тензора второго ранга, свертка дает скаляр, называемый, первым главным инвариантом или следом тензора

Свертка всегда производится по паре разновариантных индексов (один индекс должен быть верхним, а другой нижним).

Очень часто свертку комбинируют с произведением тензоров. Иногда такую комбинацию называют внутренним произведением тензоров. При этом тензоры сначала перемножают, а потом сворачивают получившийся тензор суммарного ранга. Примером может служить, использованная нами ранее запись скалярного произведения

что эквивалентно безиндексной записи

Точка, напоминающая скалярное произведение, в безиндексной записи как раз и означает совмещение умножения со сверткой. Свертка производится по соседей с точкой паре индексов. Покажем весь процесс развернуто. Из ковектора и вектора умножением образуем тензор ранга (1,1)

Свернем получившийся тензор по его единственной паре индексов

Однако не стоит считать эту точку скалярным произведением, поскольку, например вот такая операция

так же умножение совмещенное со сверткой

но по смыслу производимых действий оно эквивалентно произведению матриц, которыми представлены компоненты тензоров.

Видео:Вышмат. ТензорыСкачать

2. Симметричные и антисимметричные тензоры

Тензор называется симметричным по паре индексов, если он не изменяется при перестановке этих индексов

Если тензор не меняется при перестановке любых двух индексов, то он является абсолютно симметричным

Тензор называют антисимметричным по паре индексов, если при их перестановке тензор меняет знак

Если тензор меняет знак при перестановке любых двух индексов, то он является абсолютно антисимметричным

Любой тензор можно разложить на симметричную и антисимметричную, по выбранной паре индексов, части. Доказать это очень легко, пусть дан тензор . Проведем над ним эквивалентные преобразования

где симметричная часть тензора

а его антисимметричная часть

Чтобы не оставалось сомнений, докажем, для полученных нами тензоров, симметричность

Если говорить о тензорах второго ранга, то если таковой тензор симметричен, то он же и абсолютно симметричен. Это же касается и антисимметричного тензора второго ранга. Эти свойства следуют непосредственно из данных нами определений — у тензора второго ранга всего одна пара индексов.

Антисимметричный тензор обладает любопытным свойством. Пусть тензор второго ранга — антисимметричный. Тогда его компоненты удовлетворяют условию

данное условие выполнимо только в том случае, если диагональные компоненты тензора — нули, так как при перестановке индексов (и транспонировании матрицы компонент) диагональные компоненты переходят сами в себя. А единственное число, противоположное самому себе это ноль. Компоненты симметричные относительно главной диагонали имеют противоположные знаки.

Таким образом, из девяти компонент антисимметричного тензора второго ранга только три являются независимыми (речь идет, разумеется, о трехмерном пространстве). Три независимые компоненты образуют вектор (или ковектор). Логично предположить, что может существовать некий вектор, который однозначно зависит от данного антисимметричного тензора. Попробуем найти такой вектор.

Видео:Тензоры ВведениеСкачать

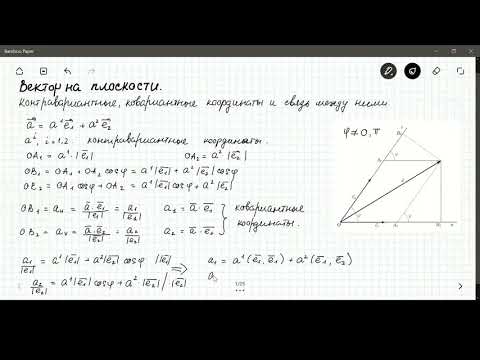
3. Сопутствующий вектор тензора второго ранга

Для того чтобы разобраться с этим вопросом я хорошенько, до перегрева клавиш на клавиатуре, «погуглил». Толкового и вместе с тем элегантного ответа на сформулированный параграфом вопрос я не нашел, поэтому предлагаю свой ответ, являющийся в некотором роде компиляцией и переработкой полученных мною сведений.

Вспомним о тензоре Леви-Чивиты, о котором я уже подробно писал тут, и построим такой тензор

Докажем, что тензор (1) — антисимметричный. Переставим в нем индексы

Минус в (2) вылез из-за того, что тензор Леви-Чивиты — абсолютно антисимметричный тензор третьего ранга. Перестановка индексов в нем, ведет к перестановке векторов базиса, на смешанном произведении которых построен данный тензор. Таким образом тензор (1) действительно антисимметричный. Тогда мы можем легко найти вектор

Примечание: о том, откуда взялись в (3) две дельты Кронекера можно прочитать в восьмой статье цикла.

соответствующий антисимметричному тензору . Тензор третьего ранга в (3), это контравариантный тензор Леви-Чивиты, который повторяет свойства ковариантного собрата с той лишь разницей, что

– для правой системы координат (для левой надо изменить знак ненулевых компонент на противоположный). Компоненты вектора (3), с учетом свойств тензора (4) определяются однозначным образом

или, если представить матрицу компонент антисимметричного тензора , то перед нами предстанет такая запись

Заметим ещё один факт, не упомянуть который нельзя, но оставив строгое доказательство за рамками данной статьи (к этому мы вернемся несколько позже). Если тензор /> является истинным тензором, то соответствующий ему вектор (3) является псевдовектором или аксиальным вектором. Псевдовектор преобразуется как и вектор при повороте координатных осей, но при смене базиса с правого на левый (или с левого на правый) — меняет своё направление на противоположное (все его компоненты меняют знак).

Если же в (1) вектор — истинный вектор, то образованный из него антисимметричный тензор является псевдотензором — компоненты такого тензора преобразуются так же как и компоненты истинного тензора при повороте осей системы координат, но меняют знак на противоположный при смене ориентации базиса.

Таким образом, любому антисимметричному тензору можно поставить в соответствии псевдовектор, получаемый в соответствии с выражением (3).

Теперь покажем, что симметричный тензор не имеет соответствующего ему псевдовектора, вернее этот псевдовектор — нулевой. Допустим, нам дан симметричный тензор , то есть справедливо равенство

Предположим, что существует вектор

Переставим индексы в (6) учитывая симметричность (5)

Выражение (7) справедливо только в одном случае, если

То есть, если мы умножим симметричный тензор на тензор Леви-Чивиты с последующей сверткой по двум парам индексов, мы получим нулевой вектор. Если мы проделаем аналогичное с произвольным тензором второго ранга

на выходе получится псевдовектор, соответствующий его антисимметричной части.

Видео:Тензорная алгебра 🔥 ранг тензора, линейные операции, умножение на вектор, умножение на тензор ☠️Скачать

Заключение

Получилось еще одно погружение в теорию тензорного исчисления. Но погружение несомненно нужное, ибо результаты, собранные в данной статье мы используем в дальнейших статьях цикла. Спасибо читателям за проявленное внимание!

Видео:Тензоры 12. Eigenchris. Тензорное произведение.Скачать

Свертка вектора и тензора

Все заявки обрабатываются в порядке живой очереди в режиме неонлайн в течение суток. Техническая поддержка сайта: 521-242

На сайте используется два типа cookies:

Основным является сессионный cookie, обычно называемый MoodleSession. Вы должны разрешить использование этого файла cookie в своем браузере, чтобы обеспечить непрерывность и оставаться в системе при просмотре сайта. Когда вы выходите из системы или закрываете браузер, этот файл cookie уничтожается (в вашем браузере и на сервере).

Другой файл cookie предназначен исключительно для удобства, его обычно называют MOODLEID или аналогичным. Он просто запоминает ваше имя пользователя в браузере. Это означает, что когда вы возвращаетесь на этот сайт, поле имени пользователя на странице входа в систему уже заполнено для вас. Отказ от этого файла cookie безопасен — вам нужно будет просто вводить свое имя пользователя при каждом входе в систему.

Некоторые курсы, возможно, открыты для гостей