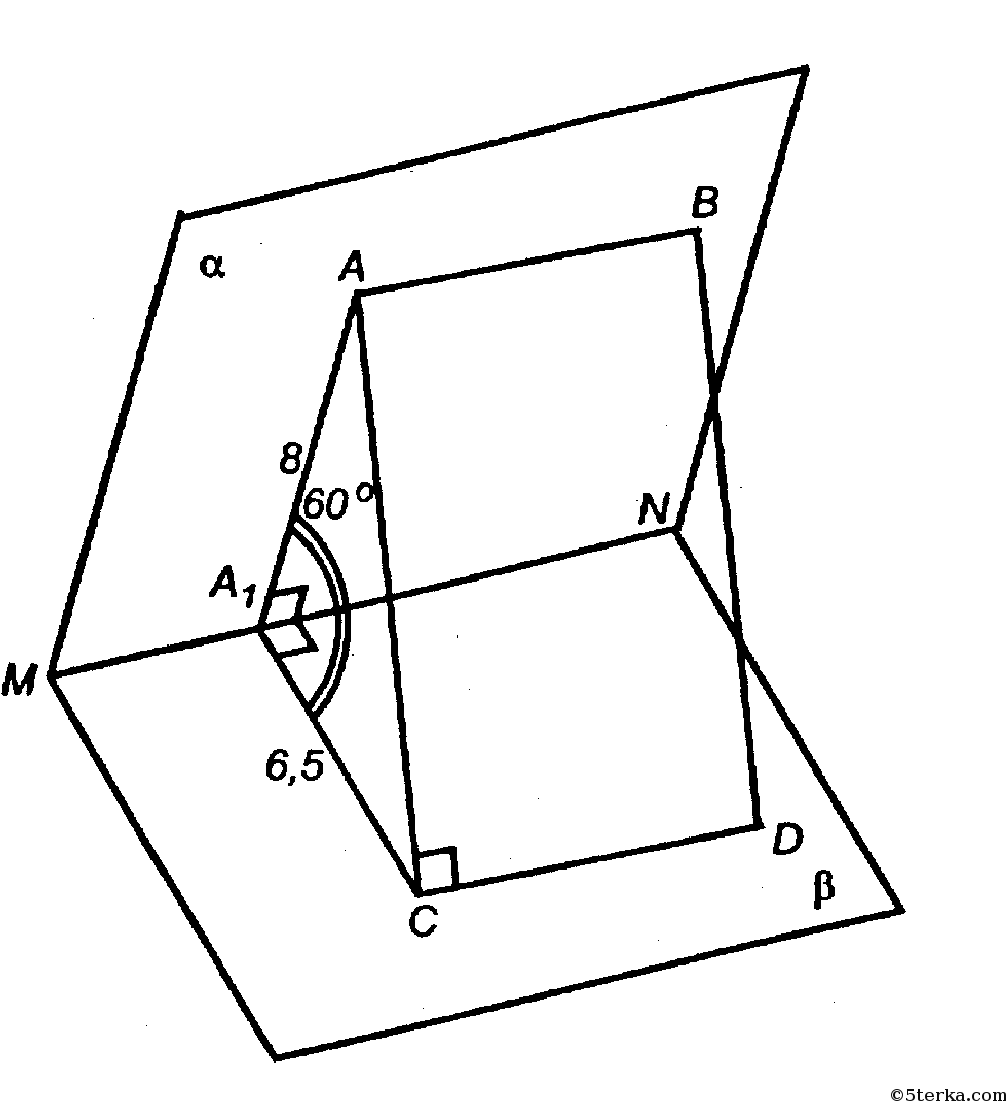
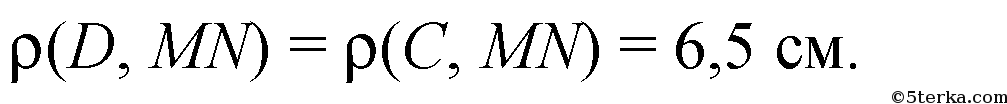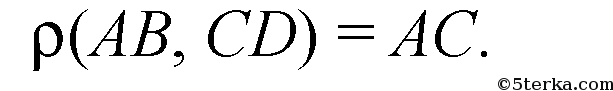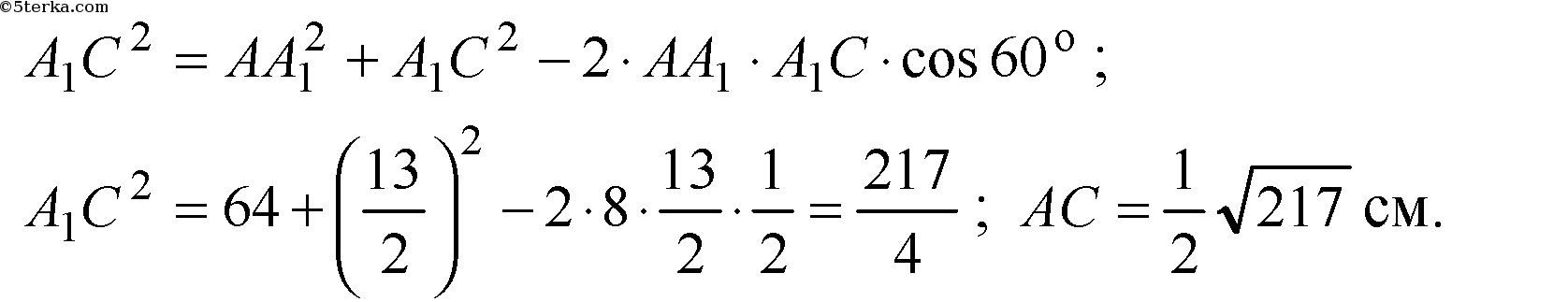Параллельные прямые аб и сд лежат в разных гранях двугранного угла (3 видео)

215. Параллельные прямые АВ и CD лежат в разных гранях двугранного угла, равного 60°. Точки А и D удалены от ребра двугранного угла соответственно на 8 см и 6,5 см. Найдите расстояние между прямыми АВ и CD.

АВ || CD — по условию, поэтому АВ || β.

По теореме II AB || MN и, значит, MN || CD.

В пл. α проводим АА₁ ⊥ MN, а в пл. β проводим А₁С ⊥ CD.

АА₁ ⊥ MN, поэтому из условий АА₁ ⊥ CD, AC₁ ⊥ CD, то по теореме о 3-х перпендикулярах АС ⊥ CD.

∠АА₁С — 60 о — линейный угол двугранного угла AMNC. По теореме косинусов для ΔА₁АС:

Ответ: 1/2√ 217 см.

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №215
к главе «Дополнительные задачи к главе II Перпендикулярность прямых и плоскостей.».

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые аб и сд лежат в разных гранях двугранного угла

Решение:
Параллельно АВ через точку Д проведём прямую, затем параллельно ВД через точку А проведём прямую. Они пересекутся в точке Е.Соединим С и Е. В треугольнике САЕ поусловию угол САЕ=120,АС= а. АЕ также=а, поскольку=ВД(по построению).Из вершины А равнобедренного треугольника АСЕ проведём высоту АК, поскольку треугольник равнобедренный она же будет и биссектрисой. Тогда угол САК=углуЕАК=60. Следовательно угол АСК=углуАЕК=30. Против угла 30° лежит катет вдвое меньший гипотенузы, значит АК=а/2. СК=КЕ=корень из(а квадрат-(а/2)квадрат)= а(корень из трёх делённое на 2). Тогда СЕ=СК+КЕ=а*корень из 3. СД= корень из (СЕквадрат+ДЕквадрат)=корень из( 3а квадрат+а квадрат)=2а.

Видео:№215. Параллельные прямые АВ и CD лежат в разных гранях двугранного угла, равного 60°. Точки А и DСкачать

Ответы к билетам по геометрии в 10 классе (стр. 2 )

Параллельные прямые аб и сд лежат в разных гранях двугранного угла

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4

2. Двугранный угол. Линейный угол двугранного угла.

3. Верно ли утверждение: если одна прямая параллельна плоскости, а другая прямая перпендикулярна этой плоскости, то прямые перпендикулярны друг другу?

Да. Пусть K — точка пересечения b и α. Параллельно перенесем прямую а так, чтобы она прошла на пл. α через т. K: K ∈ a’, a’ || a. Раз b ⊥ α, то b ⊥ a’. Отсюда заключаем, что b ⊥ a.

4. В правильной треугольной пирамиде боковое ребро образует с плоскостью основания угол 60º. Сторона основания пирамиды равна 8 см. Найдите площадь боковой поверхности пирамиды.

Ответ: S = 48 см2. (R=, l = , ha = = 4)

1. Сформулируйте определение параллельных плоскостей. Сформулируйте признак параллельности двух плоскостей.

2. Прямая призма. Сформулируйте теорему о площади боковой поверхности прямой призмы.

3. Плоскость α проходит через середины боковых сторон АВ и CD трапеции ABCD – точки M и N.
а) Докажите, что а || DA.
б) Найдите ВС, если AD=10см, NM=8см.

Плоскость, про ходящая через точки М и N, являющиеся серединами сторон будут находится на средней линии фигуры, ввиду этого образовывая прямую линию имеет свойство MN||AD||ВС; И если сия линия есть средняя линия, то сторона ВС равная Х вычисляется как (10+Х)/2=8; Х=6;

4. Дан куб ABCDA1B1C1D1. Точки К, М и Т – середины ребер СС1, В1С1 и С1D1 соответственно. Найдите АС1, если периметр сечения куба плоскостью КМТ равен см.

Сечение — равносторонний треугольник.
Сторона треугольника равна половине диагонали грани.
Зная диагональ грани, найдите ребро куба.
Зная ребро куба, найдите диагональ куба. Это и есть величина АС1.

1. Угол между прямой и плоскостью.

2. Правильная пирамида. Перечислите свойства правильной пирамиды.

3. Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости ABC. E и F – середины отрезков АВ и ВС.
а) Докажите, что CD и EF – скрещивающиеся прямые.
б) Найдите угол между прямыми CD и EF, если .

Дано: АВС,

CD-прямая, CD не лежит в плоскости (АВС)

точка Е-середина АВ
точка F — середина ВС

а) Доказать: СD и EF — скрещивающиеся;

б) найти угол между CD и EF

EF – ср. линия АВС, ЕF принадлежит (АВС),
CD не лежит (АВС), СD пересекает (АВС) в точке С, значит,

СD и EF — скрещивающиеся прямые.

EF — ср. линия ABC, след-но EF||AC, а значит угол DCA = углу между CD и EF = 60⁰

4. В правильной треугольной пирамиде сторона основания равна высоте и равна 12 см. Найдите площадь поверхности пирамиды.

1. Параллелепипед и его элементы. Сделайте чертеж и пояснения.

2. Дайте определение параллельных плоскостей. Сформулируйте свойства параллельных плоскостей. Сделайте пояснения и чертежи.

3. Точка М не лежит в плоскости трапеции ABCD (AB║CD).
а) Докажите, что треугольники MAD и MBC имеют параллельные средние линии.
б) Найдите длины этих средних линий, если AD:BC=5:3, а средняя линия трапеции равна 16см.

Если прямая параллельна хотя бы одной прямой лежащей в плоскости то она либо параллельная самой плоскости либо принадлежит ей.

Рассмотрим тр. AMD и BMC

A1D1 — сред. линия тр. AMD, не принадлежит ABCD, A1D1 || AD

B1C1 — сред. линия тр. BMC, не принадлежит ABCD, B1C1 || BC

по условию BC||AD ⇒ A1D1 || B1C1

KL — ср. линия трап. = 16 см

Введем переменную x ⇒ AD=5x, BC=3x

Тогда по формуле средней линии трапеции:

4. Дан куб ABCDA1B1C1D1. Диагональ АС1 равна .Найдите периметр сечения куба плоскостью РТН, где точки Р, Т и Н – середины ребер ВС, ВВ1 и АВ соответственно.

Ответ: РРТH =3(а=2, диагональ основания — 2, сторона равностороннего треугольника — )

1. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.

2. Сформулируйте определение скрещивающихся прямых. Сформулируйте признак скрещивающихся прямых. Сделайте чертежи и пояснения.

3. Верно ли утверждение, что все прямые, перпендикулярные к данной плоскости и пересекающие данную прямую, лежат в одной плоскости? Поясните.

Пусть

Раз

Пусть Р ∈ m. Если плоскость (PMN) проходит через перпендикуляр (РМ) к другой плоскости (α), то она перпендикулярна к этой плоскости. Итак, пл. PMN ⊥ α.

Если две плоскости (PMN и α) взаимно перпендикулярны и к одной из них (к α) проведен перпендикуляр (прямая n), имеющий общую точку (N) с другой плоскостью (PMN), то этот перпендикуляр весь лежит в плоскости (PMN).

Таким образом, любая прямая, перпендикулярная данной плоскости, лежит в плоскости PMN.

4. Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь полной и боковой поверхности призмы.

гипотенуза основания =25( теорема Пифагора, тогда площадь грани, проходящей через гипотенузу=25*h

Равновелики, значит их площади равны

1. Признак перпендикулярности прямой и плоскости.

2. Понятие многогранника. Пирамида и ее элементы. Усеченная и правильная пирамиды.

3. Через вершину А квадрата ABCD проведена прямая КА, не лежащая в плоскости квадрата.
а) Докажите, что КА и CD – скрещивающиеся прямые.
б) Найдите угол между КА и CD, если , .

а) прямые AB и CD параллельны и лежат в одной плоскости, прямая KA пересекает прямую AB в точке A следовательно она не пересекает CD( так как CD не проходит через точку A) а так как они лежат в разных плоскостях то прямые KA и CD скрещивающиеся)

б)180-85-45=50 градусов угол KAB следовательно угол между прямыми KA и AB равен 50 градусам, прямые AB и CD параллельны следовательно угол между прямыми KA и CD будет равен углы между прямыми AB и CD и равен он 50 градусам.

4. Через вершину угла Е прямоугольного треугольника НРЕ с гипотенузой НЕ проведена прямая МЕ, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки М до плоскости ЕРН, если ЕР = 5 см, а расстояние от точки М до прямой РН равно 10.