Как найти наклонную треугольника

Видео:Наклонная, проекция, перпендикуляр. 7 класс.Скачать

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

Видео:Геометрия 10 класс Атанасян №138 Как найти наклонную и проекцию если известен перпендикуляр и уголСкачать

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Наклонная к прямой

Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).

Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.

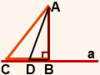
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.

Точка B — основание перпендикуляра, точка C — основание наклонной AC.

Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.

Из точки к прямой можно провести бесконечно много наклонных.

Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.

На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

В следующий раз рассмотрим свойства наклонных.

Видео:Геометрия 8. Урок 10 - Теорема Пифагора. Наклонная и проекция.Скачать

2 Comments

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Косые треугольники: характеристика, примеры, упражнения

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Содержание:

В косые треугольники Это те, у которых нет прямого угла, поэтому ни один из их внутренних углов не равен 90º. Итак, косой треугольник может быть острый угол или тупой.

В первом случае внутренние углы треугольника острые или что то же самое: меньше 90º, а во втором всегда есть угол больше 90º, то есть угол тупой. Давайте посмотрим на пример каждого из них на следующем рисунке:

Чтобы найти длины сторон и меры внутренних углов этого класса треугольников, при отсутствии прямых углов невозможно применить теорему Пифагора.

Однако есть альтернативы решению треугольника: теоремы косинусов и синусов и тот факт, что сумма внутренних углов равна 180 °.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Примеры наклонных треугольников

Руководствуясь рисунком 1, мы легко можем распознать наклонные треугольники по двум критериям, которые мы приведем ниже.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Острый треугольник

Пусть треугольник сторон a, b и c будет углом перед стороной a.

Если квадрат стороны a, противоположной острому углу α, равен Меньше чем сумма квадратов остальных сторон, треугольник равен острый угол. Алгебраически:

к 2 2 + c 2 ; α 2 > б 2 + c 2 ; α > 90º

Например, треугольник с внутренними углами 105º, 60º и 15º является тупым наклонным треугольником. Обратите внимание, что 105º + 60º + 15º = 180º.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Теоремы о синусе и косинусе

Чтобы решить наклонные треугольники, то есть найти меры всех их сторон и всех углов, требуются теоремы о синусе и косинусе.

Пусть a, b и c — стороны треугольника, а α, β и γ — его внутренние углы. Так:

Видео:Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Теорема синуса

Теорема синусов утверждает следующее:

Где α — угол, противоположный стороне a, β — угол, противоположный стороне b, а γ — угол, обращенный к стороне c.

Мы решили применить теорему синуса, когда собираемся решить треугольник, для которого известно больше углов, чем сторон.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Теорема косинусов

Согласно теореме косинусов:

c 2 = а 2 + b 2 — 2⋅a⋅b⋅cos γ

Угол γ снова находится перед стороной c. Мы также можем написать эквивалентные выражения для сторон a и b следующим образом:

к 2 = b 2 + c 2 — 2⋅b⋅c⋅cos α

б 2 = а 2 + c 2 — 2⋅a⋅c⋅cos β

Теорема косинуса предпочтительно применяется, когда известны значения двух сторон и угол между ними. Точно так же, как только три стороны треугольника известны, теорема позволяет нам вычислить косинус угла между двумя из них.

Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Решенные упражнения

Видео:Асимптоты функции. Наклонная асимптота. 10 класс.Скачать

— Упражнение 1

Убедитесь, что треугольник, стороны которого составляют 20, 10 и 12 условных единиц, тупой.

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Решение

Мы не знаем ни одного из внутренних углов, но, принимая во внимание критерий, используемый для распознавания тупых треугольников, мы можем сформулировать неравенства с квадратами сторон, чтобы проверить, истинно ли это.

Сначала находим квадраты с каждой стороны:

И мы видим, что в действительности это: 400> 100 + 144, поскольку 400> 244. Следовательно, треугольник содержит угол больше 90º, расположенный напротив стороны, которая измеряет 20. Следовательно, этот треугольник, помимо того, что он наклонен, это тоже тупо.

Видео:Как найти площадь треугольника без формулы?Скачать

— Упражнение 2.

Учитывая наклонный треугольник, показанный на рисунке 2, размеры которого даны в произвольных единицах, определите:

а) Значение х. Треугольник острый или тупой?

б) Остальные внутренние углы треугольника

Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Решение для

Известны две смежные стороны треугольника, размеры которых равны 38,0 и 45,8, а угол между ними равен 30 °, поэтому теорема косинусов имеет непосредственное применение:

Икс 2 = 38.0 2 + 45.8 2 — 2 x 38,0 x 45,8 x cos 30º = 527,18

х = (527,18) 1/2 = 22.96

Рисунок предполагает, что α> 90º и треугольник тупой и наклонный. Чтобы это проверить, находим квадраты сторон, как это было сделано в предыдущем упражнении:

Угол α больше 90 °, если квадрат на противоположной стороне: 45,8 2 больше суммы квадратов других сторон, которая равна 22,96 2 + 38.0 2 .

Посмотрим, будет ли это так:

527.18 + 1444.00 = 1971.2

Следовательно, угол α больше 90º.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Решение б

Теперь мы можем применить теорему синусов, чтобы найти один из недостающих углов. Поднимем его на угол β:

грех 30º / 22,96 = грех β / 38

sin β = 38 x (sin 30º / 22,96) = 0,8275

β = арксен (0,8275) = 55,84º

Недостающий угол можно найти, зная, что сумма внутренних углов любого треугольника равна 180 °. Таким образом:

55.84º + 30º + α = 180º

Если хотите, вы также можете использовать теорему косинусов, чтобы найти косинус угла между любыми двумя соседними сторонами. После получения функция арккосинуса используется для определения угла.

Результаты могут немного отличаться до десятичных знаков, в зависимости от выполняемого округления.

Видео:Угол наклона плоскости общего положения относительно плоскостям проекцииСкачать

Решение c

Периметр P — это контур фигуры, эквивалентный сумме измерений трех сторон:

P = 22,96 + 38,00 + 45,80 = 106,76 условных единиц.

Решение d

Формула для вычисления площади любого треугольника:

A = (1/2) x основание x высота

Нам нужно выбрать одну из сторон в качестве основы и определить высоту. Например, выбрав сторону размером 45,8, мы строим высоту час до вершины A, которая является красной линией на рисунке 2b.

Делая это, мы делим исходный треугольник на два прямоугольных треугольника, оба с час как общая нога. Любой из них работает, так как мы знаем сторону и острый угол.

Мы собираемся взять отрезок с гипотенузой, равной 38, отрезок, который измеряет час, что является искомой высотой и острым углом, равным 30º.

С помощью тригонометрических соотношений острого угла 30º определяем величину час:

sin 30º = катет напротив 30º / гипотенуза = h / 38

h = 38 x sin 30º = 19

A = (1/2) x 45,8 x 19 = 435,1 условных единиц площади.

В качестве основы мы могли бы выбрать другую из сторон, например сторону 38, в данном случае высоту час отличается, поскольку образуется еще один прямоугольный треугольник, но результат по площади такой же. Читателю остается проверить это в качестве упражнения.

— Упражнение 3.

Для треугольника ABC, такого что A = 45º, B = 60º и a = 12 см, вычислите другие данные треугольника.

Решение

Учитывая, что сумма внутренних углов треугольника равна 180º, мы имеем:

C = 180º-45º-60º = 75º.

Три угла уже известны. Затем по закону синусов вычисляются две недостающие стороны.

Возникают следующие уравнения: 12 / sin (45º) = b / sin (60º) = c / sin (75º).

Из первого равенства мы можем решить для «b» и получить, что:

b = 12 * sin (60º) / sin (45º) = 6√6 ≈ 14,696 см.

Вы также можете решить для «c» и получить:

c = 12 * sin (75º) / sin (45º) = 6 (1 + √3) ≈ 16,392 см.

— Упражнение 4.

Учитывая треугольник ABC, такой что A = 60º, C = 75º и b = 10 см, вычислите другие данные треугольника.

Решение

Как и в предыдущем упражнении, B = 180º-60º-75º = 45º. Кроме того, используя закон синусов, мы получаем, что a / sin (60º) = 10 / sin (45º) = c / sin (75º), из чего получается, что a = 10 * sin (60º) / sin (45º ) = 5√6 ≈ 12,247 см и c = 10 * sin (75º) / sin (45º) = 5 (1 + √3) ≈ 13,660 см.

— Упражнение 5.

Дан треугольник ABC такой, что a = 10 см, b = 15 см и C = 80º, вычислите другие данные треугольника.

Решение

В этом упражнении известен только один угол, поэтому его нельзя начинать, как в предыдущих двух упражнениях. Кроме того, нельзя применить закон синусов, потому что никакое уравнение не может быть решено.

Поэтому переходим к применению закона косинусов. Вот тогда:

c² = 10² + 15² — 2 (10) (15) cos (80º) = 325 — 300 * 0,173 ≈ 272,905 см,

Итак, c ≈ 16,51 см. Теперь, зная 3 стороны, используется закон синусов и получается, что:

10 / sin (A) = 15 / sin (B) = 16,51 см / sin (80º).

Следовательно, решение для B приводит к sin (B) = 15 * sin (80º) / 16,51 ≈ 0,894, что означает, что B ≈ 63,38º.

Теперь мы можем получить, что A = 180º — 80º — 63,38º ≈ 36,62º.

— Упражнение 6

Стороны наклонного треугольника равны a = 5 см, b = 3 см и c = 7 см. Найдите углы треугольника.

Решение

Опять же, закон синусов не может быть применен напрямую, поскольку никакое уравнение не может служить для получения значения углов.

Используя закон косинуса, мы имеем c² = a² + b² — 2ab cos (C), из которого при вычислении получаем cos (C) = (a² + b² — c²) / 2ab = (5² + 3²-7²) / 2 * 5 * 3 = -15/30 = -1/2 и, следовательно, C = 120º.

Теперь мы можем применить закон синусов и, таким образом, получить 5 / sin (A) = 3 / sin (B) = 7 / sin (120º), из которого мы можем решить относительно B и получить, что sin (B) = 3 * sin (120º) / 7 = 0,371, так что B = 21,79º.

Наконец, последний угол рассчитывается с использованием того, что A = 180º-120º-21,79º = 38,21º.

Ссылки

1. Клеменс, С. Геометрия с приложениями. Эддисон Уэсли.
2. Ибаньес, П. 2010. Математика III. Cengage Learning.
3. Хименес, Р. Математика II: геометрия и тригонометрия. 2-й. Издание. Пирсон.
4. Математика для вас. Тупой треугольник. Получено с: matematicasparaticharito.wordpress.com.
5. Стюарт, Дж. 2007. Precalculus. 5-е. Издание. Cengage Learning.

Что такое слезы и слезы?

Что такое самоисполняющееся пророчество? (Психология)