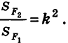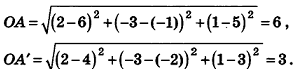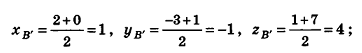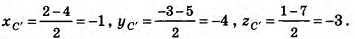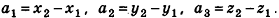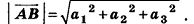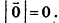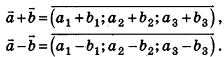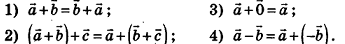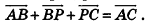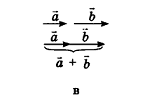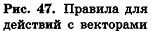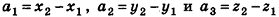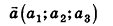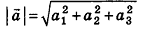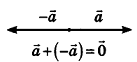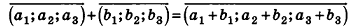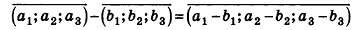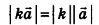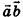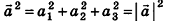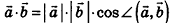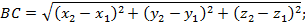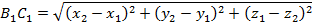О чем эта статья:
- Что такое симметрия
- Осевая симметрия
- Центральная симметрия
- Задачи на самопроверку
- Декартовы координаты в пространстве — определение и примеры с решением
- Основные задачи координат
- Движения в пространстве
- Свойства движений в пространстве
- Симметрия в пространстве
- Поворот в пространстве
- Параллельный перенос в пространстве
- Об ориентации поверхности. Лента Мебиуса
- Подобие пространственных фигур
- Преобразование подобия в пространстве
- Гомотетия в пространстве
- Логическое отношение эквивалентности
- Векторы в пространства
- Определение и свойства векторов в пространстве
- Операции над векторами в пространстве
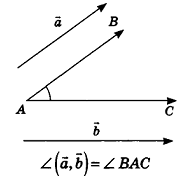
- Векторы
- Операции с векторами
- Скалярное произведение векторов
- Компланарные векторы
- Историческая справка
- Тема: Центральная и зеркальная симметрия
- 🎥 Видео
Видео:Осевая симметрия. 6 класс.Скачать

Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Видео:ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Видео:Осевая и центральная симметрия, 6 классСкачать

Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

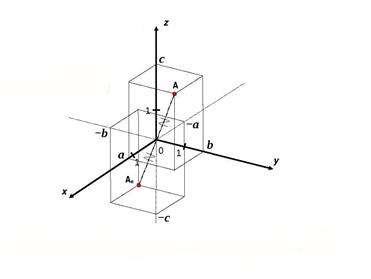
Декартовы координаты в пространстве — определение и примеры с решением
Содержание:
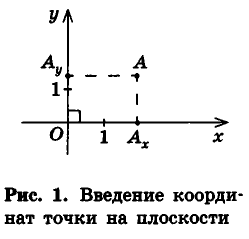
Как известно, расположение точки на координатной прямой однозначно описывается одной координатой. Из курса планиметрии вы знакомы с прямоугольной декартовой системой координат на плоскости. Напомним, что для ее введения через произвольную точку плоскости О проводят две взаимно перпендикулярные координатные оси Ох и Оу (рис. 1). При таких условиях каждой точке плоскости А ставится в соответствие упорядоченная пара чисел (х;у) — координаты оснований перпендикуляров
Вполне естественно, что для описания расположения точки в пространстве необходимо иметь три координаты — ведь, например, бабочка перемещается в воздухе не только вперед-назад и вправо-влево, но и вверх-вниз.
Итак, рассмотрим три взаимно перпендикулярные координатные оси 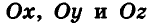
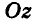
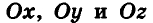
Для определения координат произвольной точки пространства А проведем из данной точки перпендикуляры 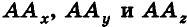
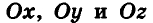
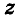
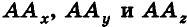
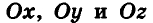
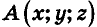
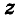
Координаты точки А можно определить и по-иному. Например, для получения координаты Ах проведем перпендикуляр АА0 к плоскости Оху, а потом из точки А0 проведем перпендикуляр 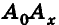
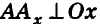
Значения координат точки А можно также получить, если провести через эту точку три плоскости, параллельные координатным плоскостям 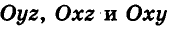
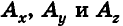
Итак, в прямоугольной декартовой системе координат каждой точке пространства ставится в соответствие единственная упорядоченная тройка чисел (x;y;z), и наоборот: каждой тройке чисел (x;y;z) соответствует единственная точка пространства.
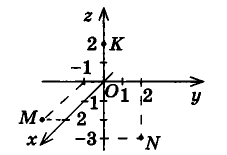
Очевидно, что если точка принадлежит одной из координатных плоскостей, то некоторая ее координата равна нулю. Так, на рисунке 4 точка М принадлежит плоскости Оху и имеет координаты (2;-1;0), а точка N плоскости Оуг — координаты (0; 2; — 3). Соответственно точки, принадлежащие координатным осям, имеют две нулевые координаты: например, координаты точки К оси Ог равны (0; 0; 2). Очевидно также, что все три координаты начала координат нулевые: 0(0;0;0). Условия, при которых та или иная координата точки равна нулю, исследуйте самостоятельно.
Пример:
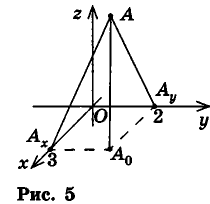
Найдите координаты проекций точки А(3;2;4) на координатные плоскости.
Решение:
Проведем из данной точки перпендикуляр АА0 к плоскости Оху и перпендикуляры ААХ и ААу к осям Ох и Оу соответственно (рис. 5). Найдем координаты точки А0.
Так как 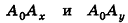
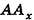
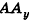
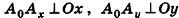
Рассуждая аналогично, определяем, что проекции точки А на плоскости Oxz и Оуz имеют координаты (3;0;4) и (0; 2; 4) соответственно.
Видео:Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Основные задачи координат
Опираясь на соответствующие свойства координат на плоскости, докажем формулы координат середины отрезка и расстояния между точками в пространстве.
Напомним, что в планиметрии каждая координата середины отрезка равна полусумме соответствующих координат его концов. Такое же свойство сохраняется и в стереометрии. Теорема (формулы координат середины отрезка в пространстве) Координаты середины отрезка вычисляются по формулам:
где 
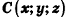
Опустим из точек А, В и С перпендикуляры на плоскость Оху. Основания этих перпендикуляров — точки 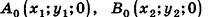
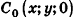
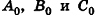
отрезка на плоскости имеем: 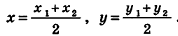
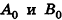
Аналогично, проведя из данных точек перпендикуляры к плоскости 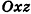
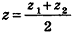
Как известно из курса планиметрии, расстояние между точками 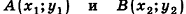
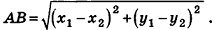
Теорема (формула расстояния между точками в пространстве) Расстояние между точками 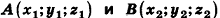
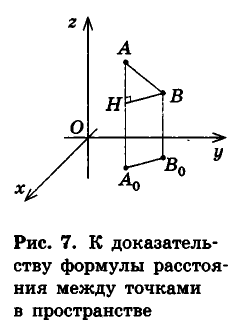
Рассмотрим сначала случай, когда отрезок АВ не параллелен плоскости Оху (рис. 7).
Опустим из точек А и В перпендикуляры 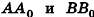
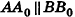
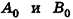
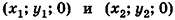
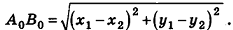
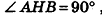
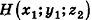
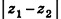
В случае, когда отрезок АВ параллелен оси 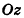
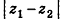
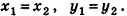
когда отрезок АВ параллелен плоскости Оху, рассмотрите самостоятельно.
Пример:
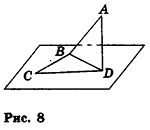
Докажите, что четырехугольник ABCD с вершинами В(4;—3; 2), C(6;3;-4), D (0; 7; -6) является параллелограммом.
Решение:
Найдем координаты середин отрезков АС и BD.
Для отрезка АС:
Для отрезка BD:
Следовательно, отрезки АС и ВD имеют общую середину. Это значит, что прямые АС и BD пересекаются, то есть точки А, В, С и D лежат в одной плоскости. Диагонали четырехугольника ABCD точкой пересечения делятся пополам, таким образом, ABCD — параллелограмм по признаку.
Отметим, что при решении аналогичной задачи в курсе планиметрии мы использовали и другой способ — доказывали попарное равенство противолежащих сторон данного четырехугольника. Но в пространстве этот способ неприемлем, так как из равенств AB = CD и AD = BC не следует, что точки А, В, С и D лежат в одной плоскости. Действительно, четырехугольник ABCD может оказаться пространственным (на рисунке 8 такой четырехугольник получен перегибом параллелограмма ABCD по прямой BD). Очевидно, что в этом случае пространственный четырехугольник ABCD удовлетворяет условиям АВ = CD и AD-ВС, но не является параллелограммом.
Второй способ решения этой задачи будет рассмотрен в § 2.
Пример:
На оси аппликат найдите точку С, равноудаленную от точек А(1;0;3) и В(4;3;-1).
Решение:
Так как искомая точка лежит на оси аппликат, то C(0;0;z). Найдем z, воспользовавшись условием АС = ВС. Имеем: 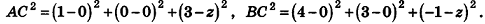
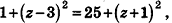
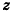
Движения в пространстве
Напомним, что движением на плоскости мы называли геометрическое преобразование, сохраняющее расстояния между точками. Так же определяют движение и в пространстве, причем все свойства движений, известные из курса планиметрии, в стереометрии сохраняются: при движении прямые переходят в прямые, лучи — в лучи, отрезки — в отрезки, и углы между лучами не изменяются.
Свойства движений в пространстве
Новым свойством движения в пространстве является то, что движение переводит плоскость в плоскость.
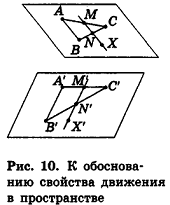
Действительно, пусть точки А, В и С, не лежащие на одной прямой, при движении переходят в точки А’, В’ и С’, также не лежащие на одной прямой (рис. 10). Покажем, что при этом движении плоскость ABC переходит в плоскость А’В’С’. Через произвольную точку X плоскости ABC проведем прямую, пересекающую две стороны треугольника ABC в точках М и N. Очевидно, что при движении эти точки перейдут в точки М’ и N’, лежащие на соответствующих сторонах треугольника А’В’С’. Таким образом, прямая M’N’, в которую переходит прямая MN, принадлежит плоскости А’В’С’, то есть точка Х’ в которую переходит точка X, принадлежит прямой M’N’, а следовательно, и плоскости А’В’С’. Это значит, что произвольная точка плоскости ABC при движении переходит в точку плоскости А’В’С’.
Аналогично можно доказать, что каждую точку плоскости А’В’С’ можно получить из точки плоскости ABC при рассматриваемом движении. Итак, при движении плоскость ABC переходит в плоскость А’В’С’.
Так же как и на плоскости, в пространстве две фигуры называются равными, если они совмещаются движением.
Симметрия в пространстве
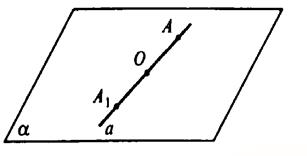
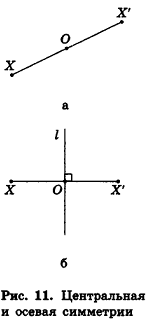
Симметрия как один из видов геометрических преобразований знакома вам из курса планиметрии. Преобразования симметрии относительно точки (центральная симметрия) и относительно прямой (осевая симметрия) в пространстве определяют так же, как и на плоскости:
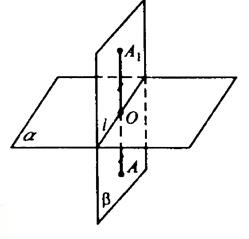
- точки X и X’ называются симметричными относительно точки О, если точка О — середина отрезка XX’ (рис. 11, а); точка О называется центром симметрии;
- точки X иХ’ называются симметричными относительно прямой I, если эта прямая перпендикулярна отрезку XX’ и проходит через его середину (рис. 11, б); прямая I называется осью симметрии.
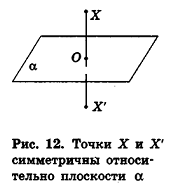
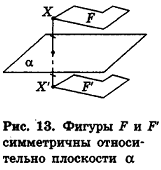
Рассмотрим еще один вид симметрии в пространстве. Пусть а — фиксированная плоскость, X — произвольная точка вне ее. Проведем перпендикуляр ХО к плоскости а и на луче ХО отложим отрезок ОХ’, равный ХО, но лежащий в другом полупространстве относительно плоскости а (рис. 12). Мы получили точку X’, симметричную точке X относительно плоскости а.
Определение:
Точки X и X’ называются симметричными относительно плоскости а, если эта плоскость перпендикулярна отрезку XX’ и проходит через его середину. Точки плоскости а считаются симметричными сами себе.
При этом плоскость а называется плоскостью симметрии.
Очевидно, что точкой, симметричной точке X’ относительно плоскости а, является точка X.
Определение:
Преобразованием симметрии (симметрией) относительно плоскости а называется такое преобразование фигуры F в фигуру F, при котором каждая точка X фигуры F переходит в точку X’ фигуры F’, симметричную X относительно плоскости а.
При этом фигуры F и F’ называются симметричными относительно плоскости а (рис. 13).
Наглядно представить симметрию относительно плоскости можно с помощью плоского зеркала. Любой объект и его изображение симметричны относительно плоскости зеркала (рис. 14). Поэтому симметрию относительно плоскости иначе называют зеркальной симметрией.
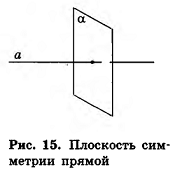
Если преобразование симметрии относительно плоскости а переводит фигуру F в себя, то такая фигура называется симметричной относительно плоскости а, а сама плоскость а — плоскостью симметрии фигуры F. Например, плоскостью симметрии прямой является любая перпендикулярная ей плоскость (рис. 15).
Центры, оси и плоскости симметрии фигуры, если они у нее есть, называются элементами симметрии этой фигуры.
Несложно доказать, что точки, симметричные точке A(x;y;z) относительно координатных плоскостей, осей и начала координат, имеют следующие координаты:
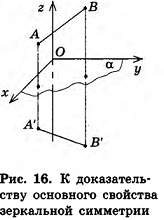
Теорема (основное свойство зеркальной симметрии) Зеркальная симметрия является движением.
Пусть точки А и В при симметрии относительно плоскости а переходят в точки А’ и В’ соответственно. Введем систему координат так, чтобы плоскость Оху совпала с а (рис. 16).

Так как точки, симметричные относительно плоскости Оху, имеют одинаковые абсциссы и ординаты, но противоположные аппликаты, то для точек 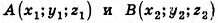
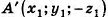
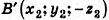
Таким образом, АВ = А’В’. Значит, зеркальная симметрия сохраняет расстояния между точками, то есть является движением.
Из доказанной теоремы следует, что зеркальная симметрия обладает всеми свойствами движения.
Пример №1
Докажите, что если две прямые зеркально симметричны, то они лежат в одной плоскости.
Решение:
Рассмотрим произвольные точки А к В прямой а, которые при зеркальной симметрии относительно плоскости а переходят в точки А’ и В’ прямой а’. По определению симметрии относительно плоскости 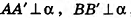
Самые разнообразные виды пространственной симметрии мы наблюдаем в живой и неживой природе, искусстве, технике и т. д. В основе строения живых форм лежит принцип симметрии, причем природа гармонично объединяет различные виды симметрий с почти математической строгостью (рис. 17).
Совершенную симметричную форму имеют природные многогранники — кристаллы (подробнее рассмотрим их в § 12). Физики утверждают, что симметрия является фундаментальным свойством природы, с которым связаны законы сохранения энергии и импульса, строение атомов и молекул, а также особенности природных явлений.
Невозможно переоценить значение симметрии в искусстве. В древнегреческой архитектуре симметрия была воплощением законов целесообразности и гармонии (рис. 18). Идеи зеркальной симметрии широко отражены в живописи Средневековья.
В литературных произведениях существует симметрия образов, ситуаций, мышления. Вспомним хотя бы «закон мести» в греческой трагедии: виновник преступления в конце концов сам становится жертвой такого же преступления.
Яркими примерами симметрии образов являются персонажи комедии Н. В. Гоголя «Ревизор» Добчинский и Бобчинский — сам автор отмечает, что они чрезвычайно похожи друг на друга (рис. 19). Симметричными можно считать и литературные образы героев-антиподов, противостояние между которыми составляет основной конфликт литературного произведения: Шерлок Холмс и профессор Мориарти у А. Конана Дойля, доктор Джекил и мистер Хайд у P. JI. Стивенсона и т. д.
В музыке построение отдельных мелодичных форм также подчиняется законам симметрии. Прослушайте «Рондо-каприччио» великого Бетховена — композитор использует основную тему как своеобразную плоскость симметрии, от которой как бы отражаются отдельные эпизоды и вариации. Симметрия в музыке наглядно проявляется даже через нотную запись (рис. 20).
Глава I. Координаты, векторы и геометрические преобразования в пространстве
Неисчерпаемые возможности симметрии и то широкое применение, которое она получила в разных областях человеческой деятельности, подтверждают универсальность геометрических знаний и значимость геометрии в общечеловеческой культуре.
Поворот в пространстве
Напомним, что на плоскости мы выполняли поворот фигуры вокруг данной точки О в заданном направлении на данный угол. Но в пространстве такое описание поворота не является однозначным: действительно, через фиксированную точку О проходит бесконечно много плоскостей, и в каждой из них поворот фигуры вокруг точки О на данный угол приведет к различным результатам.
Между тем, открывая дверь или переворачивая страницу книги, мы поворачиваем все точки фигуры в одном направлении на определенный угол, причем все точки некоторой прямой остаются неподвижными. Попробуем на основании этих наглядных примеров приблизиться к строгому определению поворота в пространстве.
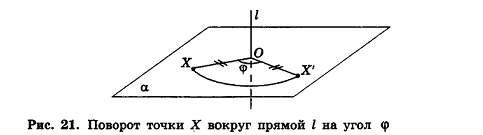
Для этого рассмотрим фиксированную прямую I и произвольную точку X (рис. 21). Проведем через точку X плоскость а, перпендикулярную I, и обозначим точку О пересечения плоскости а с прямой I. В плоскости а выполним поворот точки X вокруг точки О на угол ф, т. е. построим точку X’ так, чтобы 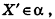
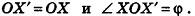
Напомним, что на плоскости мы характеризовали поворот и направлением — по часовой стрелке или против часовой стрелки. В пространстве направление поворота на плоскости а зависит от выбора стороны, с которой мы смотрим на эту плоскость (об этом, в частности, речь будет идти в п. 2.5). Поэтому договоримся считать прямую, вокруг которой выполняется поворот, ориентированной
(т. е. осью с заданным направлением) и рассматривать поворот по часовой стрелке или против часовой стрелки, если смотреть на плоскость с положительного направления этой оси. Например, на рисунке 22 показано направление поворота точек плоскости а вокруг оси I против часовой стрелки.
Поворотом фигуры F вокруг ориентированной прямой I на угол ф называется преобразование фигуры F в фигуру F’, при котором каждая точка X фигуры F (Х&1) переходит в точку X’ фигуры F так, что 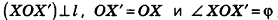
Все углы измеряются по часовой стрелке (или все — против часовой стрелки), точки прямой I при повороте переходят сами в себя.
Иначе говоря, при повороте вокруг ориентированной прямой I каждая точка фигуры F смещается в заданном направлении на данный угол по дуге окружности, плоскость которой перпендикулярна прямой I, центр принадлежит этой прямой, а радиус равен расстоянию от данной точки фигуры F до прямой I. На рисунке 23 фигура F переходит в фигуру F’ при повороте вокруг оси I на угол ф против часовой стрелки.
Прямую I называют осью поворота (или осью вращения), а угол ф — углом поворота.
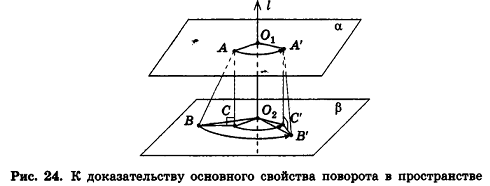
(основное свойство поворота в пространстве) Поворот вокруг прямой является движением.
Пусть при повороте вокруг оси I на угол ф (0° 180° рассмотрите самостоятельно.
Если при повороте вокруг некоторой прямой I фигура F переходит в себя, то говорят, что эта фигура имеет поворотную симметрию (или симметрию вращения). Примеры пространственных фигур, обладающих поворотной симметрией, будут рассмотрены дальше.
Заметим также, что поворот вокруг прямой I на 180° является осевой симметрией относительно прямой I (докажите это самостоятельно).
Параллельный перенос в пространстве
Параллельный перенос в пространстве является разновидностью параллельного проектирования для случая, когда плоскость проектируемой фигуры параллельна плоскости проекции (или совпадает с ней).
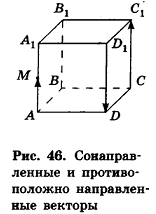
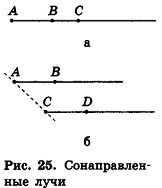
Напомним, что сонаправленными лучами мы называли:
- два луча одной прямой, один из которых является частью другого (например, лучи АС и ВС на рис. 25, а);
- два параллельных луча, лежащих в плоскости по одну сторону от прямой, проходящей через их начальные точки (например, лучи АВ и CD на рис. 25, б).
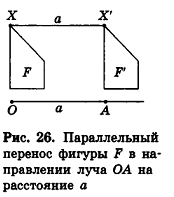
Определение параллельного переноса в стереометрии ничем не отличается от планиметрического. Параллельным переносом, фигуры F в направлении луча OA на расстояние а называется преобразование фигуры F в фигуру F’, при котором каждая точка X фигуры F переходит в точку X’ фигуры F’ так, что лучи XX’ и OA сонаправлены и XX’ = а (рис. 26).
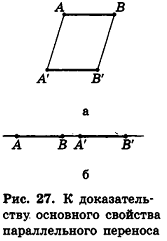
Теорема (основное свойство параллельного переноса в пространстве)
Параллельный перенос в пространстве является движением.
Пусть при параллельном переносе точки А и В переходят в точки А’ и В’ соответственно. Покажем, что АВ = А’В’ Если точки А, В, А’ и В’ не лежат на одной прямой (рис. 27, а), то отрезки АА’ и ВВ’ параллельны и равны. Отсюда АА’В’В — параллелограмм, то есть АВ = А’В’ как противолежащие стороны параллелограмма. В случае, когда точки А, В, А’ и В’ лежат на одной прямой (рис. 27, б), получаем:
В дальнейшем, изучая векторы в пространстве, мы будем рассматривать параллельный перенос на вектор 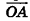
Убедитесь самостоятельно в том, что рассмотренное доказательство справедливо и для других случаев расположения точек А, В, А и В’ на одной прямой.
Параллельный перенос переводит прямую в параллельную прямую (или в себя), отрезок — в равный ему отрезок, угол — в равный ему угол.
Параллельный перенос переводит плоскость в параллельную плоскость (или в себя).
Действительно, поскольку параллельный перенос является движением, то он переводит произвольную плоскость а в плоскость 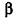
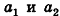
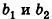
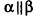
Так же как и на плоскости, в пространстве при условии введения системы координат (рис. 29) параллельный перенос, который переводит точку M(x;y;z) в точку M'(x’;y’;z’), можно задать формулами:
где 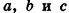
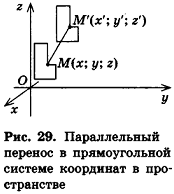
Пример №2
Докажите, что четырехугольник ABCD с вершинами А(-2;1;0), В(4;-3;2), С(б;3;-4), £>(0;7;-б) является параллелограммом.
Решение:
Покажем, что параллельный перенос, который переводит точку В в точку С, переводит точку А в точку D (рис. 30). Сначала найдем формулы этого переноса. Подставив в общие формулы параллельного переноса координаты
точек В и С, получим уравнения, из которых определим а, b и с: 6 = 4 + а; 3 = -3+b; -4 = 2+ с. Отсюда а = 2; b = 6; с = -6.
Следовательно, искомый перенос задается формулами
Подставив в эти формулы координаты точек А и D, получим правильные равенства: 0 = -2+2, 7 = 1+6, -6=0-6.
Так как по условию ABCD — четырехугольник, его вершины не лежат на одной прямой. Следовательно, по свойству параллельного переноса в четырехугольнике ABCD две стороны параллельны и равны, то есть ABCD — параллелограмм.
Об ориентации поверхности. Лента Мебиуса
При рассмотрении преобразования поворота было отмечено, что направление поворота в данной плоскости фактически зависит от выбора стороны, с которой мы смотрим на плоскость. Такой выбор стороны называется ориентацией плоскости.
Аналогично можно определить понятие ориентации и для других двусторонних поверхностей в пространстве (поверхности куба, цилиндра, шара и др.). Представим себе, что мы закрасили одну из сторон рассматриваемой поверхности — очевидно, что другая ее сторона останется незакрашенной.
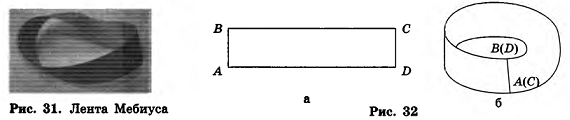
Но эта очевидность только кажущаяся, так как существуют поверхности, которые невозможно ориентировать. Самой простой из них является так называемая лента Мебиуса (рис. 31), открытая в 1858 году немецким астрономом и математиком Августом Мебиусом. Изготовить ее модель очень просто: для этого бумажную ленту, имеющую форму прямоугольника ABCD (рис. 32, а), нужно склеить так, чтобы вершина А совместилась с вершиной С, а вершина В — с вершиной D (рис. 32, б).
Удивительно, но лента Мебиуса является односторонней поверхностью. Чтобы убедиться в этом, попробуйте начать закрашивать ленту с любого места, постепенно перемещаясь по ее поверхности, —
Глава I. Координаты, векторы и геометрические преобразования в пространстве в результате вся поверхность окажется закрашенной. Значит, муравьям, которые ползут по ленте Мебиуса на гравюре М. Эшера (рис. 33), не нужно переползать через край ленты, чтобы попасть на ее «противоположную сторону».
Еще одно интересное свойство ленты Мебиуса заключается в том, что она имеет только один край. Действительно, если выбрать в любом месте края ленты точку и начать от нее двигаться вдоль края, со временем мы вернемся в ту же исходную точку, причем все точки края будут пройдены (проверьте это самостоятельно).
И наконец, предлагаем вам еще один эксперимент: проведите на ленте Мебиуса среднюю линию (т. е. отрезок, который соединяет середины противолежащих сторон АВ и CD прямоугольника, из которого была склеена лента) и попробуйте разрезать по ней ленту. Оказывается, что вместо двух отдельных частей получается дважды перекрученная лента Мебиуса. Невероятно, но это так!
Лента Мебиуса стала первым примером неориентированной поверхности. Позднее были открыты и другие — например, так называемая бутылка Клейна (рис. 34).
Свойство односторонности ленты Мебиуса нашло довольно широкое техническое применение. В XX веке такую ленту использовали для записи звука на непрерывную магнитную пленку, а также как красящую ленту в первых (матричных) принтерах. Ременные передачи или ленты конвейера, имеющие форму ленты Мебиуса, применяют и сегодня, ведь такие ленты служат вдвое дольше, чем обычные, так.как изнашиваются вдвое медленнее (объясните почему). В современной математике существует специальный раздел «топология», в котором рассматриваются, в частности, формы и ориентация поверхностей. А в мировой культуре лента Мебиуса остается символом удивительных открытий, которые до сих пор скрывает геометрия.

Подобие пространственных фигур
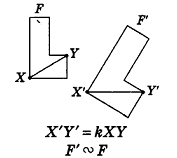
Так же как и на плоскости, преобразование фигуры F в пространстве называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одном и том же отношении. Это значит, что если две произвольные точки X и Y фигуры F при преобразовании подобия переходят в точки X’ и У’ фигуры F’, то X’Y’ = kXY , где k — коэффициент подобия (k > 0).
Преобразование подобия в пространстве
Преобразование подобия в пространстве переводит прямые в прямые, лучи — в лучи, отрезки — в отрезки, а также сохраняет углы между лучами (доказательство этих свойств в стереометрии не отличается от планиметрического). Новым свойством подобия в пространстве является то, что преобразование подобия переводит плоскости в плоскости (докажите это утверждение самостоятельно, аналогично соответствующему обоснованию для движения в п. 2.1).
Две фигуры в пространстве называются подобными, если они переводятся одна в другую преобразованием подобия. Напомним некоторые свойства подобия.
- Любая фигура подобна сама себе:
(рефлексивность подобия).
- Если
(симметричность подобия).
- Если
(транзитивность подобия).
- Отношение площадей подобных фигур равно квадрату коэффициента подобия: если
с коэффициентом k, то
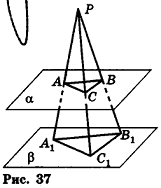
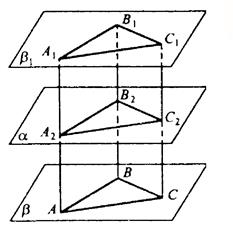
Пример №3
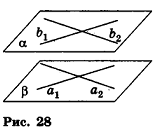
Через точку Р проведены три луча, не принадлежащие одной плоскости и пересекающие параллельные плоскости а и 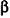
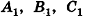
Решение:
Согласно свойству параллельных плоскостей плоскость РАВ пересекает плоскости 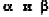
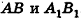
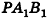
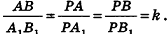
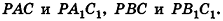
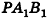
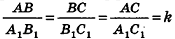
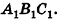
Гомотетия в пространстве
Напомним, что гомотетией с центром в точке О и коэффициентом k>0 называется такое преобразование фигуры F в фигуру F, при котором каждая точка X фигуры F переходит в точку X’ фигуры F’, лежащую на луче ОХ, и ОХ’ = кОХ.
Гомотетия является преобразованием подобия (доказательство этого факта в стереометрии аналогично планиметрическому). Докажем еще одно свойство гомотетии в пространстве.
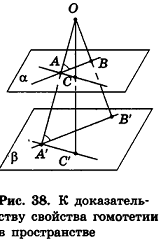
Теорема (свойство гомотетии в пространстве)
Гомотетия переводит плоскость, не проходящую через центр гомотетии, в параллельную плоскость или в себя.
Пусть а — данная плоскость, точка О — центр гомотетии. Рассмотрим случай, когда коэффициент гомотетии h не равен единице (рис. 38).
Данная гомотетия переводит любые точки А и В плоскости а в точки А’ и В’ соответственно, причем 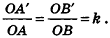
Аналогично, рассматривая в плоскости а прямую АС, пересекающуюся с АВ, можно доказать, что при гомотетии она переходит в параллельную прямую А’С’. Следовательно, при данной гомотетии плоскость а переходит в плоскость а’, содержащую точки А, В’ и С’. Так как А’В’ || АВ и А’С || АС , а плоскости а и а’ не совпадают, то по признаку параллельности плоскостей а’||а.
Очевидно, что в случае k = l плоскость а при гомотетии переходит в себя. Теорема доказана.
Ясно, что плоскость, проходящая через центр гомотетии, при этом преобразовании также переходит в себя.
Обратим внимание и на такой интересный факт (даем его без доказательства): если две фигуры подобны, то одну из них можно получить из другой путем последовательного применения гомотетии и движения.
Пример №4
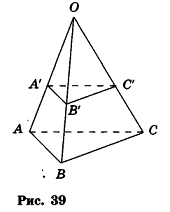
При гомотетии с центром О (2; — 3; 1) треугольник ABC переходит в треугольник А’В’С’. Найдите координаты точек В’ и С’, если А(б;-1;5), А'(4;-2;3), В(0;1;7), С(-4;-5;-7).
Решение:
Найдем длины отрезков OA и OA’:
Так как по определению гомотетии OA’ = kOA, то k = 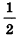
По формулам координат середины отрезка получаем:
Следовательно, B'(l;-1;4), С'(-1;-4-3).
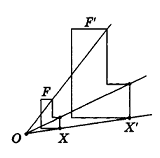
Подобие пространственных фигур находит широкое применение на практике. Например, архитекторы и строители, проектируя размещение новых зданий и сооружений на местности, предлагают заказчикам макеты строящихся объектов (рис. 40).
Логическое отношение эквивалентности
Как мы уже отмечали, отношение подобия на множестве геометрических фигур является рефлексивным, симметричным и транзитивным. Эти три свойства присущи и некоторым другим отношениям, причем не только геометрическим.
Например, для любых двух натуральных чисел а и b можно рассматривать отношение «число а дает при делении на 5 тот же остаток, что и число Ь» (обоснуйте самостоятельно рефлексивность, симметричность и транзитивность такого отношения). На множестве людей указанные свойства имеет отношение «а является гражданином той же страны, что и b» (если не принимать во внимание людей без гражданства и людей с двойным гражданством), а на множестве слов русского языка — отношение «слово а имеет тот же корень, что и слово b.
В логике отношения, имеющие свойства рефлексивности, симметричности и транзитивности, называют отношениями эквивалентности. Наличие такого отношения на множестве однородных предметов позволяет разделить их на классы эквивалентности — подмножества, элементы которых имеют общие свойства. Например, отношение подобия на множестве многоугольников позволяет нам рассматривать как отдельные классы равносторонние треугольники, квадраты и т. д. Действительно, все фигуры одного класса имеют общие геометрические свойства, которые сохраняются при преобразовании подобия. О таких фигурах. говорят, что они являются равными с точностью до подобия (другими словами, имеют одинаковую форму, но отличаются размерами). Для изучения геометрических свойств фигур определенного класса достаточно рассмотреть одну произвольную фигуру и на ее примере исследовать особенности остальных фигур данного класса.
Деление на классы эквивалентности используют не только математики. Так, филологи, рассматривая для существительных русского языка отношение «слова а и b имеют одинаковые окончания при склонении», делят все существительные на три склонения. Идея деления на классы эквивалентности лежит в основе многих химических и биологических классификаций. Вспомните, как использовал эту идею в периодической таблице химических элементов Д. И. Менделеев.
Векторы в пространства
Большинство понятий и утверждений для векторов непосредственно переносятся в стереометрию из планиметрии. Напомним основные положения соответствующей геометрической теории, подробно останавливаясь на тех из них, которые в пространстве выглядят иначе, чем на плоскости.
Определение и свойства векторов в пространстве
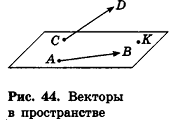
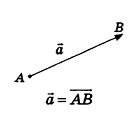
Как известно из курса геометрии 9 класса, вектором, называется направленный отрезок. Направление вектора (от начала к концу) на рисунках обозначают стрелкой. Вектор, начало и конец которого совпадают, называется нулевым. Нулевой вектор не имеет какого-либо определенного направления. На рисунке 44 изображены ненулевые векторы 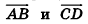
Нулевой вектор часто обозначают 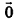
Так же как и на плоскости, ненулевой вектор в пространстве характеризуется не только направлением, но и длиной. Это позволяет рассматривать параллельный перенос в направлении луча АВ на расстояние, равное длине отрезка АВ, как параллельный перенос на вектор 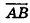
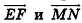
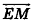
Так как положение точки в пространстве задается тремя координатами, дополняется определение координат вектора.
Определение:
Координатами вектора 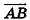
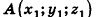
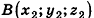
Соответственно длина (модуль) вектора 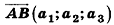
Нулевой вектор имеет нулевые координаты, и его длина равна нулю:
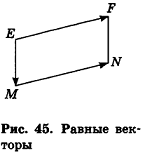
Так же как и на плоскости, в пространстве равные векторы имеют равные координаты, и наоборот: если у векторов соответствующие координаты равны, то эти векторы равны.
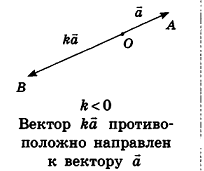
Напомним, что ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
В свою очередь, среди коллинеарных векторов различают сонаправленные и противоположно направленные. Если лучи АВ и CD сонаправлены, то ненулевые векторы 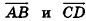
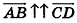
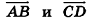
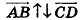
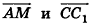
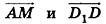
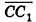
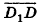
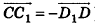
Пример №5
Даны точки А (-7; 4; 2) и В(-2;0;-l). Найдите координаты кондов вектора 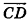
Решение:
Пусть 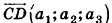
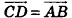
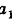
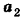
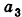
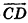
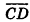
Операции над векторами в пространстве
Операции сложения и вычитания для векторов в пространстве определяют аналогично тому, как их вводили на плоскости. Итак, для векторов 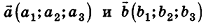
Так же сохраняются в пространстве и соответствующие свойства этих операций. Для любых векторов 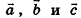
Доказательство утверждений 1-4 несложно получить с помощью геометрических построений аналогично тому, как это проводилось на плоскости.
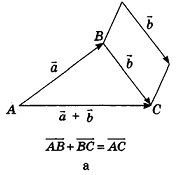
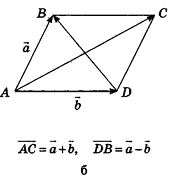
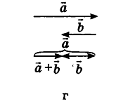
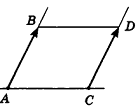
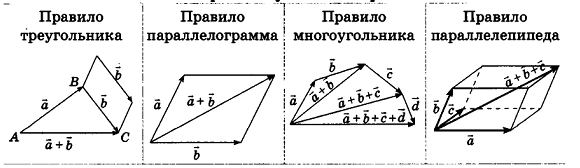
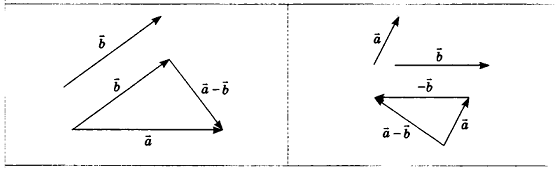
Для действий с неколлинеарными векторами в геометрической форме в пространстве, как и на плоскости, можно воспользоваться правилом треугольника (рис. 47, а) и правилом параллелограмма (рис. 47, б). Правила сложения двух коллинеарных векторов иллюстрирует рисунок 47, в, г.
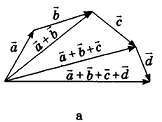
Обобщением правила треугольника для сложения нескольких векторов является правило многоугольника (рис. 48, а). Особенность его применения в пространстве заключается в том, что векторы-слагаемые не обязательно принадлежат одной плоскости (то есть многоугольник, который получается при построении вектора-суммы, может быть пространственным). Например, на рисунке 48, б в тетраэдре РАВС получим векторное равенство
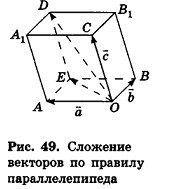
Опишем еще одно правило, которое служит для. сложения трех векторов в пространстве. Пусть векторы-слагаемые 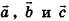
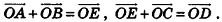
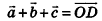
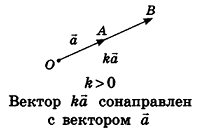
Произведением вектора 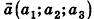
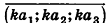
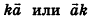
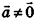
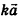
Преобразование подобия переводит прямые в прямые, отрезки — в отрезки, плоскости — в плоскости, а также сохраняет углы между лучами X’Y’ = kXY
Гомотетией с центром в точке О и коэффициентом k (k>0) называется такое преобразование фигуры F в фигуру F’, при котором каждая точка X фигуры F переходит в точку X’ фигуры F, лежащую на луче ОХ, и ОХ’ = кОХ
Число k называют коэффициентом гомотетии, а фигуры F и F’ — гомотетичными
Основное свойство гомотетии: гомотетия является преобразованием подобия
Гомотетия переводит плоскость, не проходящую через центр гомотетии, в параллельную плоскость или в себя
Векторы
Вектором называется направленный отрезок
Координатами вектора с началом в точке 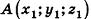
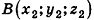
Длина (модуль) вектора 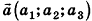
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых
Векторы 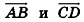
Векторы 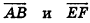
Противоположными векторами называются два противоположно направленных вектора одинаковой длины
Два вектора называются равными, если они совмещаются параллельным переносом
От любой точки можно отложить вектор, равный данному, и притом только один Критерии равных векторов:
- векторы сонаправлены и имеют равные длины;
- векторы имеют равные координаты
Операции с векторами
Сложение векторов
Суммой векторов 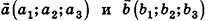
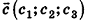
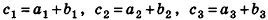
Построение суммы векторов
Вычитание векторов
Разностью векторов 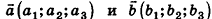
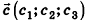
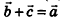
Построение разности векторов
Умножение вектора на число
Произведением вектора 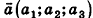
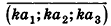
Если 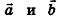
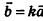
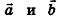
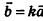
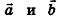
У коллинеарных векторов соответствующие координаты пропорциональны, и наоборот: если у двух векторов соответствующие координаты пропорциональны, то эти векторы коллинеарны
Скалярное произведение векторов
Скалярным произведением векторов 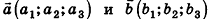
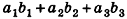
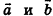
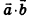
Скалярное произведение 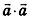
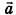
Скалярное произведение векторов равно произведению их длин на косинус угла между ними:
Свойство и признак перпендикулярных векторов: если 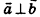
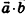
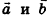
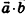
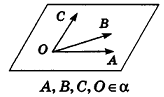
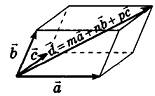
Компланарные векторы
Ненулевые векторы называются компланарными, если при откладывании их от одной и той же точки они лежат в одной плоскости
Любой вектор d можно разложить по трем некомпланарным векторам 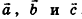
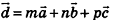
Историческая справка
Эпоха великих географических открытий и обусловленное ими развитие производства, торговли, мореплавания стали толчком к возникновению аналитической геометрии. Этот раздел геометрии, основанный на введении прямоугольных координат и установлении соответствия между алгебраическими уравнениями и геометрическими фигурами, стал итогом многолетних математических исследований.
Создателями аналитической геометрии считают французских ученых Рене Декарта (1696-1650) и Пьера Ферма (1601-1665). Ферма в начале XVII века, занимаясь восстановлением утраченных работ древнегреческих ученых, в частности Аполлония Пергского, определил общий подход к изучению геометрических мест точек через алгебраические уравнения. Открытие Декартом системы координат на плоскости позволило создать математический аппарат для воплощения идей аналитической геометрии. Но как Ферма, так и Декарт только говорили о возможности использования координат в пространстве. Трехмерную систему координат первым начал применять французский математик Алексис Клод Клеро (1713-1765), а систематическое изложение аналитической геометрии в пространстве представил в 1748 году выдающийся ученый Леонард Эйлер.
В историю аналитической геометрии вписаны также имена украинских ученых. Уроженец Винни-чины Виктор Яковлевич Буняковский (1804-1889) учился математике в Париже, у ведущих ученых своего времени — Коши, Лежандра, Пуассона, Лапласа, а позднее работал в Петербурге. Он был автором около ста работ по математическому анализу, алгебре, геометрии, теории чисел и теории вероятностей. Так, известное вам неравенство а-6
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Центральная симметрия. 6 класс.Скачать

Тема: Центральная и зеркальная симметрия
Выполнила ученица 11 А класса Ковалева Дарья
Учитель Багирян Нонна Александровна
· определение и основные свойства
· фигуры, обладающие центральной симметрией
· применение в жизни
· определение и построение
· фигуры, обладающие зеркальной симметрией
· зеркальная симметрия в реальной жизни
Центральной симметрией называют преобразование пространства относительно точки A , переводящее точку X в такую точку X′, что A — середина отрезка XX′. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре.Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
· Центральная симметрия является движением;
· Любая прямая при центральной симметрии преобразуется в прямую. Причем, прямая, проходящая через центр, преобразуется в себя. Прямая, не проходящая через центр, преобразуется в параллельную ей прямую. (доказано в задаче 2)
· Центральная симметрия сохраняет расстояния между точками.
· Центральная симметрия переводит отрезки в отрезки, лучи в лучи.
Докажем, что центральная симметрия является движением.
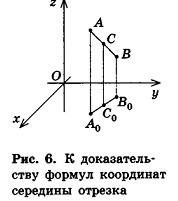
Обозначим буквой O центр симметрии и введем в прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек M (x; y; z) и M₁ (x₁; y₁; z₁), симметричных относительно точки О.
Если точка М не совпадает с центром О, то О – середина отрезка ММ₁. По формулам координат середины отрезка получаем 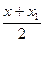
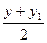
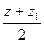
Рассмотрим теперь две точки А (x₁; y₁; z₁) и В (x₂; y₂; z₂) и докажем, что расстояние между симметричными им точкам А₁ и В₁ равно АВ. Точки А₁ и В₁ имеют координаты А₁ (-x₁; -y₁; -z₁ ) и В₁ (-x₂; -y₂; -z₂). По формуле расстояния между двумя точками находим: 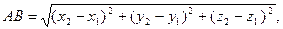
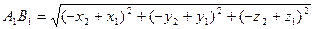
Построим точку А₀ симметричную точке А относительно точки О.
Пусть А (a; b; c). Тогда координаты A₀ (-a; -b; -c).
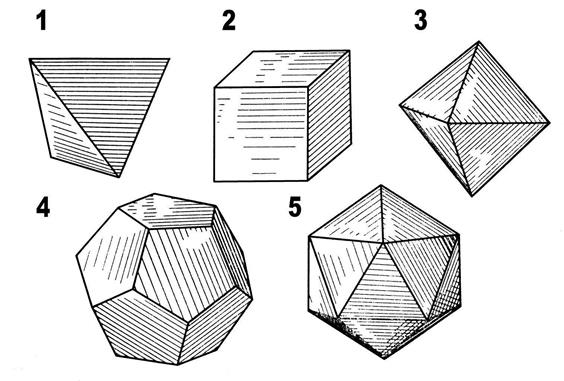
Фигуры, обладающие центральной симметрией.
1. – тетраэдр 2. – куб 3. – октаэдр 4. – додекаэдр 5. – икосаэдр
Применение центральной симметрии в жизни.
В архитектуре центральная симметрия используется реже осевой. Она присуща античным круглым храмам, используется в колоннах.
Колизей Пирамиды в Египте
Башни церквей, замков, колонны проектировались с учетом центральной симметрии. Такие сооружения предавали зданиям массивности. Башни одинаково роскошно выглядели с любой плоскости города.
Центральная симметрия в природе. Она присутствует в снежинках, листьях деревьев и трав, насекомых, цветах, животных.
Центральная симметрия прослеживается в
костюмах казанских татар
№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при центральной симметрии относительно начала координат.
При центральной симметрии относительно начала координат знаки координат искомых точек меняются на противоположные.
А (0; 1; 2) → А₁ (0; -1; -2)
В (3; -1; 4) → В₁ (-3; 1; -4)
С (1; 0; -2) → С₁ (-1; 0; 2)
№ 2. Докажите, что при центральной симметрии: а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую; б) прямая, проходящая через центр симметрии, отображается на себя.
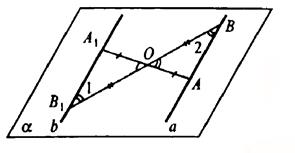
Через центр симметрии и данную прямую можно провести единственную плоскость. Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а. Пусть А ∈ а, построим отрезок ОА.
Продолжим ОА за точку О на расстояние ОА1=АО. Получим точку А1, симметричную А.
Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ1=ОВ. Получим точку B1, симметричную точке В.
Через А1 и В1 проведем прямую b. Рассмотрим ΔAОВ и ΔА1ОВ1⋅AО=А1О, ВО=ОВ1, ΔАОВ=ΔА1ОВ1 как вертикальные, следовательно, ΔAОВ=ΔА1ОВ1.
Тогда, ∠1=∠2 и а || b.
Пусть А ∈ а. Симметричная ей точка А1 тоже принадлежит прямой а; АО=ОА1.
Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.
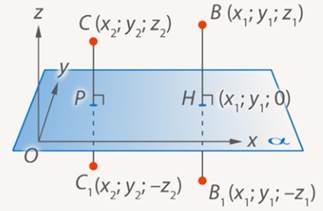
Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М₁ относительно плоскости α.
Докажем, что зеркальная симметрия является движением.
Для этого введем прямоугольную систему координат Оxyz так, чтобы плоскость Oxy совпала с плоскостью симметрии, и установим связь между координатами точек 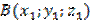
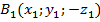
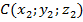
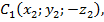
Найдем длину отрезков BC и B₁C₁ по формуле расстояния между точками:
Отсюда BC = B₁C₁, значит, зеркальная симметрия является движением.
Отсюда следует, что зеркальная симметрия обладает следующими свойствами:
· переводит прямые в прямые
· полупрямые – в полупрямые
· отрезки – в отрезки
· плоскости – в плоскости
· сохраняет углы между прямыми.
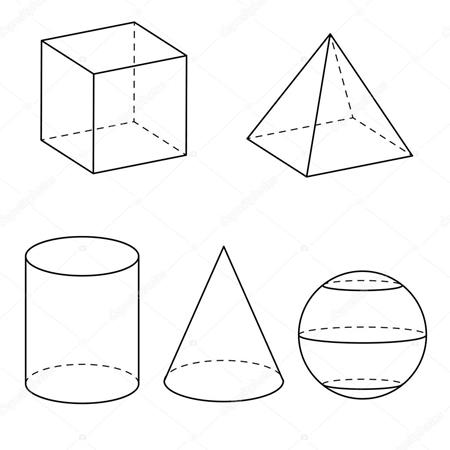
Фигуры, обладающие зеркальной симметрией
(слева на право) – куб, пирамида, цилиндр, конус, сфера
Зеркальная симметрия в жизни
Наиболее распространена вархитектуре зеркальная симметрия.
Эйфелева башня Тадж Махал
Зеркальная симметрия в природе может быть представлена отражением изображения в воде.
Животные, растения, и человек тоже могут послужить примерами зеркальной симметрии. Однако назвать их идеальными примерами сложно, ведь даже лицо человека, которое на первый взгляд может показаться симметричным, таковым не является.
№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при зеркальной симметрии относительно координатных плоскостей.
Если плоскость симметрии — плоскость Оxy, то меняем значение координаты z на противоположную (т.к. ось Оz перпендикулярна плоскости Оxy, О – точка их пересечения)
А (0; 1; 2) → А₁ (0; 1; -2)
В (3; -1; 4) → B₁ (3; -1; -4)
С (1; 0; -2) → C₁ (1; 0; 2)
Аналогично решение с другими плоскостями.
Если плоскость симметрии — плоскость Оyz, то меняем значение координаты x.
А (0; 1; 2) → А₁ (0; 1; 2)
В (3; -1; 4) → B₁ (-3; -1; 4)
С (1; 0; -2) → C₁ (-1; 0; -2)
Если плоскость симметрии — плоскость Оxz, то меняем значение координаты y.
А (0; 1; 2) → А₁ (0; -1; 2)
В (3; -1; 4) → B₁ (3; 1; 4)
С (1; 0; -2) → C₁ (1; 0; -2)
№ 2. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β₁. Докажите, что если: а) β || α, то β₁ || α; б) β ┴ α, то β₁ совпадает с β.
а) Выберем три точки в плоскости А, В, С, не лежащие на одной прямой. Проведем АА2⊥α, ВВ2 ⊥α, СС2 ⊥α. Продолжим эти отрезки за точки А1, B1, C1 так, что А2А1=АА2, B2B1=BB2, C2C1=CC2.
Плоскость β1 проходит через точки А1, В1 и C1, она — единственная.
Если две пересекающиеся прямые (ВА и ВС) одной плоскости (β) параллельны двум прямым (B1A1 и В1С1) другой плоскости (β1), то эти плоскости параллельны: β1 || β.
б)
Пусть α⊥β. Возьмем произвольную точку А ∈ β и построим АО перпендикулярно плоскости α. Продолжим отрезок за точку О на расстояние ОА1=АО.
Две плоскости взаимно перпендикулярны и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, тогда этот перпендикуляр весь лежит в этой плоскости, т.е.
АО⊂β, следовательно, и АА1 ⊂β.
Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая тоже принадлежит плоскости β. тогда, плоскость β отображается сама на себя, или β1 совпадает с β.
🎥 Видео
Симметрия относительно точки (центральная симметрия). Пример 2Скачать

Осевая и центральная симметрия.Скачать

6 класс, 26 урок, СимметрияСкачать

Ось симметрииСкачать

Симметрия относительно точки. 6 классСкачать

Симметрия относительно точки, линии. Математика 6 класс. Подготовка к ЕГЭ, ОГЭ, ЦТ, экзаменуСкачать

Построение проекции вектора на осьСкачать

Центральная и осевая симметрии. Геометрия 7 класс.Скачать

Симметрия относительно прямойСкачать

11 класс, 10 урок, Осевая симметрияСкачать

Симметрия относительно прямой (осевая симметрия). Пример 2Скачать

48. Осевая и центральная симметрииСкачать

Симметрия относительно точки (центральная симметрии). Пример 1Скачать













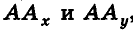
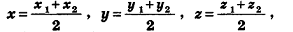
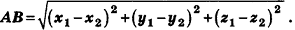
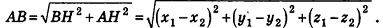
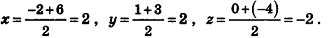
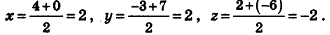

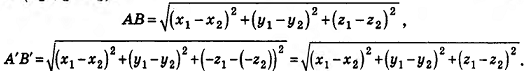




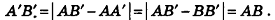
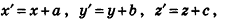

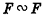 (рефлексивность подобия).
(рефлексивность подобия).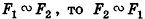 (симметричность подобия).
(симметричность подобия).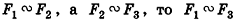 (транзитивность подобия).
(транзитивность подобия).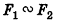 с коэффициентом k, то
с коэффициентом k, то