Дата добавления: 2014-09-25 ; просмотров: 9864 ; Нарушение авторских прав
Контрольные вопросы по теории
1. При каких условиях считают, что множество разбито на классы?
2. Как определить число элементов в объединении двух или трех конечных множеств?
1.Из множества Р = выделили подмножества А, В и С. Выясните, в каком случае произошло разбиение множества Р на классы:
2.Выясните, в каких случаях классификация выполнена правильно:
а) треугольники делятся на прямоугольные, тупоугольные и остроугольные;
б) треугольники делятся на разносторонние, равнобедренные и равносторонние;
в) углы делятся на острые, прямые и развернутые;
г) целые числа можно разбить на натуральные числа, число 0 и отрицательные целые числа;
д) натуральные числа делятся на однозначные, двузначные и трехзначные;
е) параллелограммы могут быть прямоугольниками, квадратами и ромбами.
3.Из множества Т треугольников выделили два подмножества: Х – прямоугольных треугольников и Y – равнобедренных треугольников. Постройте для данных множеств круги Эйлера и установите, на сколько непересекающихся областей разбился круг, изображающий множество Т. Все множества, изображенные этими областями, задайте описанием характеристического свойства.
4.Разбейте множество четырехугольников на классы: а) по какому-либо одному свойству; б) по двум свойствам. Укажите эти свойства, для каждого случая постройте круги Эйлера, установите число непересекающихся областей и выясните, какие множества изображаются этими областями.
5.Множества Р ромбов, Т треугольников и К многоугольников, имеющих угол 30°, являются подмножествами множества М многоугольников. Постройте круги Эйлера для данных множеств, установите, на сколько непересекающихся областей разбился круг, изображающий множество М, и для всех множеств, изображенных этими областями, укажите характеристическое свойство
6.Из множества натуральных чисел выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 4. Постройте круги Эйлера для указанных множеств; установите, на сколько попарно непересекающихся множеств произошло разбиение множества натуральных чисел; укажите характеристические свойства этих множеств.
7.Из множества параллелограммов выделили подмножество прямоугольников и подмножество квадратов. Постройте круги Эйлера для данных множеств. На сколько попарно непересекающихся множеств произошло разбиение множества параллелограммов; укажите характеристические свойства этих множеств.
8.Из 25 учащихся класса 15 увлекаются математикой, а 12 – русским языком. Каким может быть число учащихся, увлекающихся обоими предметами; только одним предметом?
9.Из 25 учащихся класса 12 увлекаются математикой, а 8 – русским языком. Каким может быть число учащихся, увлекающихся обоими предметами; только одним предметом?
10.Из 30 учащихся класса 22 занимаются в математическом кружке, 11 – в кружке «Умелые руки», а 5 – в обоих кружках. Сколько учащихся класса не занимаются ни в том, ни в другом кружке?
11.Из 100 учащихся класса, изучающих английский и немецкий языки, 85 изучают английский, 45 – немецкий. Сколько человек изучают оба языка?
12.В классе 30 человек, посещающих факультативные занятия по естествознанию и математике. Известно, что углубленно изучают оба предмета 10 человек, а математику – 25. Сколько человек посещают факультативные занятия только по естествознанию?
13.В классе 28 учеников. Из них 12 лыжников, 10 пловцов, 18 велосипедистов, причем каждый спортсмен занимается ровно двумя видами спорта. Сколько в классе спортсменов? Сколько учеников не занимаются спортом?
14.Все 35 первокурсников являются читателями институтской или районной библиотеки. Из них 25 берут книги в институтской библиотеке, 20 – районной. Сколько из них: а) не являются читателями институтской библиотеки; б) не являются читателями районной библиотеки; в) являются читателями только институтской библиотеки; г) являются читателями только районной библиотеки; д) являются читателями обеих библиотек?
15.Из 100 человек английский язык изучают 28, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 5, немецкий и французский – 7. Все три языка изучают 3 студента. Сколько студентов изучает только один язык?
16.Сколько чисел содержится в множестве Р, если известно, что среди них 100 чисел кратно двум; 115 – трем; 120 – пяти; 45 – шести; 38 – десяти; 50 – пятнадцати; 20 чисел – тридцати?
17.Из 100 студентов 6 отличников, 20 спортсменов и 25 участников «Весны ГГПИ». Из них отличников и спортсменов – 3; спортсменов и артистов – 2; отличников и артистов – 2, отличников, спортсменов и артистов – 1. Сколько студентов не являются ни отличниками, ни спортсменами, ни артистами?
18.В классе 35 учеников, каждый из которых любит футбол, волейбол или баскетбол. Из них 24 человека любят футбол, 18 – волейбол, 12 – баскетбол. 10 учеников любят футбол и волейбол, 8 – футбол и баскетбол, а 5 – волейбол и баскетбол. Сколько учеников этого класса любят все три вида спорта?
19.Из 50 человек 20 занимаются плаванием, 25 – хоккеем, 6 – только волейболом, 4 – ни одним видом спорта. Сколько человек занимаются плаванием и хоккеем?
20.В спартакиаде участвует школьная команда из 20 человек, каждый из которых имеет разряд по одному или нескольким видам спорта: легкой атлетике, плаванию или гимнастике. Известно, что 12 человек имеют разряд по легкой атлетике, 10 – по гимнастике, 5 – по плаванию. Сколько учеников имеют разряды по всем трем видам спорта, если по легкой атлетике и гимнастике имеют разряд 4 человека, по плаванию и гимнастике – 2 человека, по легкой атлетике и плаванию – 2 человека?
21.80 человек знают хотя бы один из трех языков, причем 10 человек знают только английский, 14 – только немецкий, 20 – только французский, а число знающих все три языка на 2 меньше числа знающих только немецкий и французский, на 4 меньше числа знающих только английский и французский, на 6 меньше числа знающих только английский и немецкий. Сколько человек знают все три языка?
22.Одному из учащихся было поручено написать заметку в стенную газету об успеваемости класса за первое полугодие. Он взял журнал и выписал следующие сведения: из 40 учащихся класса 25 человек не имеют троек по русскому языку, 28 – по математике, 31 – по чтению, 22 – по чтению и русскому языку, 12 человек учатся без троек по всем предметам. Прочитав заметку, редактор сказал: «Ты ошибся в счете, данные явно неверные». Объясните, почему представленные сведения не могут быть верными?
23.В одной школе из 70 десятиклассников 26 человек занимаются в радиотехническом кружке, 18 – в математическом, 24 – в физическом, 20 человек не занимаются ни в каком кружке. Из членов физического кружка 10 посещают математический кружок и 6 радиотехнический. Есть ли ученики, посещающие только радиотехнический и математический кружки?
Тема 4. Соответствия между двумя множествами
Контрольные вопросы по теории
1. Дайте определение декартова произведения множеств.
2. Перечислите способы задания декартова произведения множеств.
3. В каком отношении находятся множества X × Y и Y × X?
4. Что называют соответствием между множествами Х и Y?
5. Какое множество называют областью отправления, областью прибытия, областью определения и множеством значений соответствия?
6. Перечислите способы задания соответствий.
7. Какое соответствие называют отображением множества Х в множество Y; отображением множества Х на множество Y?
8. Какое соответствие называют взаимно однозначным соответствием?
9. Какие множества называют равномощными? В каком случае равномощны конечные множества?
10. Какие множества называют счетными? Приведите примеры счетных и несчетных множеств.
1.Запишите все двузначные числа, цифры десятков которых принадлежат множеству А = , а цифры единиц — множеству В = .
3.Изобразите на координатной плоскости элементы декартова произведения множеств X и Y, если:
е) X = R, Y = [–2; 2];
ж) X = (–3; 2], Y =R;
4.На координатной плоскости постройте прямую, параллельную оси ОХ и проходящую через точку Р (–2; 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.
5.На координатной плоскости постройте полосу, ограниченную прямыми, проходящими через точки (–2; 0) и (2; 0) и параллельными оси ОY. Опишите множество точек, принадлежащих этой полосе.
6.На координатной плоскости постройте прямоугольник с вершинами в точках А (–3; 5), В (–3; 8), С (7; 5), D (7; 8). Опишите множество точек этого прямоугольника.
8.Найдите декартово произведение множеств А = и В = и выделите из него подмножество пар, которое задает соответствие: а) «больше»; б) «меньше»; в) «меньше на 1»; г) «меньше в 3 раза».
9.Даны множества А = и В = . Между ними установлено соответствие «число а больше числа b», а Î А, b Î В. Постройте граф и график этого соответствия.
10.На рисунках изображены графы соответствий между множествами А и В. Для каждого соответствия укажите область отправления, область прибытия, область определения и множество значений. Какое из соответствий является отображением множества А в множество В, отображением множества А на множество В, взаимно однозначным отображением множества А на множество В?
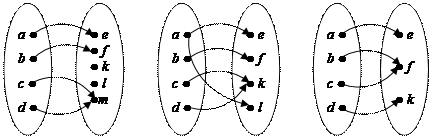
11.Между элементами множеств Х и Y задано соответствие. Определите, является ли оно отображением. Если является, то выясните, какого вида это отображение.
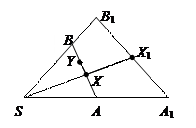
12.Точке М отрезка АВ сопоставляется ее проекция M1 на прямую р. Покажите, что в этом случае отрезок АВ отображается в прямую р. Каким будет образ отрезка АВ при этом отображении?
13. 
14.Каждой точке X окружности соответствует точка Х1 диаметра АВ, что XX1 ^ АВ. Задано ли при этом отображение окружности на диаметр? Является ли оно взаимно однозначным?
15.Докажите, что множества А и В равномощны, если: а) А – множество букв в слове «колос», В – множество цифр числа 34 574; б) А – множество дней недели, В – множество, элементами которого являются буквы а, b, с, d, e, f, k.
16.Приведите примеры множеств, равномощных множеству: а) ног у кошки; б) цифр от 0 до 9.
17.Прочитайте следующие высказывания о множествах А и В и укажите истинные: а) если А = В, то А
18.Даны две окружности с общим центром О, между которыми задано отношение: точке А окружности с меньшим радиусом ставится в соответствие точка A1 другой окружности, которая лежит на луче ОА. Установите, является ли это соответствие отображением одной окружности на другую. Сделайте вывод о равномощности данных окружностей.
19.X – множество окружностей плоскости, Y – множество точек этой плоскости. Отношение между множествами X и Y задано так: «окружность х имеет центр у». Равномощны ли множества X и Y?
20.Выделите из множества натуральных чисел четыре равномощных ему подмножества.
21.Докажите, что данные множества являются счетными: а) нечетных натуральных чисел; б) целых неотрицательных чисел; в) квадратов натуральных чисел; г) натуральных чисел, кратных 5.
Тема 5. Числовые функции
Контрольные вопросы по теории
1. Дайте определение числовой функции. Перечислите способы задания функций.
2. Какое множество называют областью определения и множеством значений функции?
3. Какое множество точек координатной плоскости называют графиком функции?
4. Дайте определения постоянной функции, прямой пропорциональности, обратной пропорциональности, линейной функции, квадратичной функции и укажите их свойства.
1.Каждому числу из множества Х = поставлен в соответствие его делитель из множества натуральных чисел. Является ли это отношение функцией?
2.Какие из следующих формул задают на множестве действительных чисел функцию: а) у = 4х; б) у = 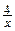
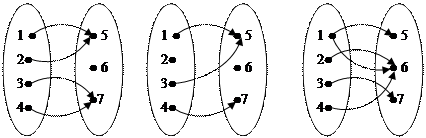
3.На рисунке изображены графы различных соответствий. Найдите среди них те, которые задают функции. Для каждой функции укажите область определения и множество значений.
4.Функция задана уравнением у = 3х – 1. Областью ее определения является множество . Найдите множество значений этой функции.
5.Найдите множество значений функции у = 4 – х 2 , если ее областью определения является множество Х: а) Х = R; б) Х = (– 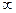
6.Найдите область определения функции: а) у = х + 2; б) у = 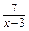
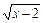
7.Постройте график функции у = 3х, зная, что ее область определения есть: а) множество действительных чисел; б) числовой отрезок [0, 4]; в) множество целых чисел; г) множество .
8.Постройте график функции у = 2х и выясните, какими свойствами обладает функция.
9.Постройте график функции у = 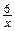
10.Какие из нижеприведенных таблиц задают прямую или обратную пропорциональность:
| а) | х | г) | х |
| у | у | ||
| б) | х | д) | х |
| у | у | ||
| в) | х | е) | х |
| у | у |
11.Установите вид зависимости, в которой находятся переменные х и у, если:
а) х – длина стороны квадрата, у – его периметр;
б) х– длина стороны квадрата, у – его площадь;
в) х – число страниц, перепечатываемых машинисткой за один час, у – число часов, за которое она перепечатывает рукопись;
г) х – число прочитанных страниц книги, у – число оставшихся непрочитанными.
12.Используя понятие прямой и обратной пропорциональности, обоснуйте способы решения нижеприведенных задач, рассматриваемых в начальных классах:
а) Из каждых 10 м ситца получались 3 рубашки. Сколько таких рубашек можно сшить из 50 м ситца?
б) Скорость машины 60 км/ч, скорость велосипедиста в 5 раз меньше. Велосипедист проехал расстояние от села до железнодорожной станции за 2 ч. За сколько минут можно проехать это расстояние на машине?
в) Два столяра, один из которых работал 6 дней, а второй – 3 дня, отремонтировали по одинаковому количеству стульев. По сколько стульев в день ремонтировал второй столяр, если известно, что первый ремонтировал по 10 стульев в день?
г) 400 кг печенья упаковали в коробки, по 5 кг в каждую. Сколько понадобится коробок, если в каждую из них упаковывать в 2 раза больше печенья?
д) Велосипедист ехал со скоростью 12 км/ч и был в пути 2 ч. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 4 км/ч?
е) Два опытных участка имеют одинаковую площадь. Ширина первого участка 30 м, ширина второго – 40 м. Найдите длину первого участка, если известно, что длина второго участка равна 75 м.
13.Постройте график функции у = – 2х + 6 и выясните, какими свойствами обладает функция. Установите, на какое множество данная функция отображает промежуток [0, 3].
14.С турбазы на станцию, отстоящую от нее на 20 км, отправился турист со скоростью 4 км/ч. На каком расстоянии (s км) от станции он будет через t ч? Напишите уравнение, выражающее зависимость между s и t. Какую функцию задает это уравнение?
15.Постройте графики квадратичных функций (разными способами) и выясните, какими свойствами обладает функция:
Тема 6. Отношения на множестве
Контрольные вопросы по теории
1. Дайте определение бинарного отношения на множестве Х.
2. Как записать утверждение о том, что элементы х и у находятся в отношении R?
3. Перечислите способы задания отношений.
4. Сформулируйте свойства, которыми могут обладать отношения. Как данные свойства отражаются на графе?
5. Какими свойствами должно обладать отношение, чтобы оно являлось отношением эквивалентности?
6. Как отношение эквивалентности связано с разбиением множества на классы?
7. Какими свойствами должно обладать отношение, чтобы оно являлось отношением порядка?
1.Приведите примеры отношений, существующих между: а) натуральными числами; б) множествами; в) прямыми на плоскости; г) треугольниками.
2.Какие из знаков >, +, ¹, ³, ×, ^, –1 ?
10.На множестве отрезков заданы отношения «длиннее», «длиннее в 2 раза», «длиннее на 2 см». Как задать отношения, обратные данным?
11.Постройте граф отношения «легче, чем» между элементами множества . Известно, что заяц тяжелее собаки, кролик легче поросенка, а собака тяжелее поросенка. Кто легче: кролик или собака? Кто тяжелее: поросенок или заяц? Кто из животных самый легкий и самый тяжелый?
12.Мы наблюдаем за вертолетом, орлом, дирижаблем и самолетом. Орел находится выше вертолета, вертолет – ниже самолета, но выше дирижабля, а орел – ниже самолета. Постройте граф отношения «быть выше» и выясните, в каком порядке расположились по высоте вертолет, орел, дирижабль и самолет.
13.Из лагеря вышли 5 туристов. Мы назовем их не в том порядке, в котором они идут один за другим: Вася, Галя, Толя, Лена и Миша. Толя идет впереди Миши, Лена – впереди Васи, но позади Миши, Галя – впереди Толи. Кто идет первым и кто идет последним? Кто идет вслед за Мишей и кто идет перед Мишей?
14.В нашем лесу каждый занимается своим делом и этому делу обучает других: одни плетут корзины, другие ловят рыбу. Ремеслу мы научились друг у друга. Кот учился у Выдры, Еж – у Зайца, Лиса – у Волка, Мышь – у Ежа. Бобер учил Волка и Выдру, Заяц – Белку, а Барсук – Зайца. Бобер был учеником Медведя, а Еж – учителем Дятла. Лучше всех плел корзины Еж. Чем занимается Заяц, Дятел, Волк и Лиса? Кто из зверей нашего леса раньше всех научился ловить рыбу и кто плести корзины?
15.Дано множество А = <а; b; с>, между элементами которого задано отношение Т. Постройте граф данного отношения и выясните, какими свойствами оно обладает, если:
16.Дано множество Е = <а; b; с; d>, между элементами которого имеет место отношение Р, такое что а Р b, а Р а, b Р b, с Р с, с Р d, с Р а, d P d, d P а. Постройте граф данного отношения и выясните, какими свойствами оно обладает.
17.На множестве X = задано отношение S = . Определите свойства отношения S и постройте его график.
18.Отношение «быть делителем» задано на множестве Х = . Постройте граф этого отношения и проверьте его свойства.
19.На множестве Х = заданы отношения: Р: «меньше», Т: «меньше на 2», М: «меньше или равно». Постройте графы данных отношений и проверьте их свойства.
20.Каковы свойства отношений «больше в 2 раза» и «больше на 2», заданных на множестве Х = ? В чем сходство графов данных отношений?
21.На множестве А = заданы отношения «больше» и «кратно». В чем их сходство и различие?
22.Проверьте все свойства отношения Р, заданного на множестве Х, если:
а) Р: «х и у живут в одном доме», Х – множество людей;
б) Р: «х кратно у», Х – множество натуральных чисел;
г) Р: «отрезок х длиннее у», Х – множество отрезков;
д) Р: «х учитель у», Х – множество людей;
з) Р: «х ³ у», Х – множество натуральных чисел;
и) Р: «быть старше», Х – множество студентов группы.
23.На множестве отрезков заданы отношения Р: «длиннее» и М: «иметь одну и ту же длину». Какое из них является отношением эквивалентности?
24.Х – множество прямых на плоскости. Какие из следующих отношений в множестве Х являются отношениями эквивалентности: а) «прямая х параллельна прямой у»; б) «прямая х перпендикулярна прямой у»; в) «прямая х пересекает прямую у».
25.А – множество точек плоскости, l – прямая на этой плоскости, R – отношение «точки х и у симметричны относительно оси l». Докажите, что R отношением эквивалентности не является.
27.В множестве М студентов педагогического факультета задано отношение R – «учиться на одном курсе». Докажите,что R – отношение эквивалентности. На какие классы разобьется множество М этим отношением?
29.На множестве А = задано отношение «быть делителем». Упорядочивает ли оно множество А?
30.Сформулируйте свойства отношений «равно», «меньше», «не больше», «меньше на 2», заданных на множестве Х = , и постройте их графы. Какое из этих отношений является отношением: а) эквивалентности; б) порядка?
31.Какие из следующих отношений являются отношениями эквивалентности, а какие – порядка:
а) иметь большую площадь на множестве прямоугольников;
б) подобие на множестве геометрических фигур;
в) равносильность на множестве уравнений;
г) быть выше по рейтингу на множестве студентов группы?
32.В начальном курсе математики на множестве натуральных чисел рассматриваются отношения «больше», «больше на несколько единиц», «больше в несколько раз», «непосредственно следует за». Какие из них упорядочивают множество натуральных чисел?
Тема 7. Предикаты и операции над ними
Контрольные вопросы по теории
1. Что называется высказывательной формой или предикатом?
2. Какие различают предикаты по числу входящих в них переменных? Приведите примеры.
3. Какое множество называют областью определения предиката?
4. Какое множество называют множеством истинности предиката?
5. Что называют конъюнкцией предикатов? Докажите равенство, связывающее область истинности конъюнкции предикатов с областями истинности этих предикатов.
6. Дайте определения дизъюнкции, отрицания, импликации предикатов. Запишите равенства, связывающие области истинности конъюнкции предикатов с областями истинности этих предикатов.
1.Среди следующих предложений укажите высказывания и предикаты и поясните свой ответ. а) 2 – натуральное число. б) Разность чисел х и 3 равна 7. в) 2 3 > 3 2 . г) х = 11 является решением неравенства 2х – 1 > 5. д) 3у + 5 2 – 1 = 0. и) Число делится на 5. к) Для всех чисел х и у верно равенство х + у = у + х. л) Будьте здоровы! м) Некоторые студенты не выполнили домашнее задание. н) х 2 – 7х + 2.
2.На множестве Nзадан предикат С (х): «число х – делитель 12». Сформулируйте высказывания С (4), С (5), С (8) и найдите их значения истинности.
3.На множестве Z задан предикат В (у): «у + 3 у» задан на множестве R. Назовите две пары чисел, при подстановке которых в предикат получается: а) истинное высказывание; б) ложное высказывание.
5.Изменится ли множество истинности предиката А (х): «х 2 – 4х – 5 = 0», если в качестве возможных значений переменной х рассмотреть: а) множество R; б) множество N?
6.Найдите множества истинности следующих предикатов:
21.На рисунке изображены множества истинности предикатов А (х) и В (x). В каком случае предикаты А (х) и В (x) являются отрицаниями друг друга?
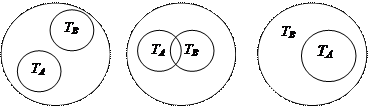
22.Известно, что Т А Ç Т В Ç Т С ≠ Æ. Заштрихуйте множества истинности следующих предикатов: а) 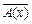
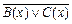
Тема 8. Высказывания с кванторами. Отрицание высказываний, содержащих кванторы
Контрольные вопросы по теории
1. Как можно предикат превратить в высказывание?
2. Приведите примеры слов, которые используются в качестве кванторов общности и существования.
3. Укажите способы установления значения истинности высказываний, содержащих кванторы?
4. Как построить отрицание высказываний, содержащих кванторы?
1.Среди следующих предложений выделите высказывания. а) 7 0.
д) Для любого значения х найдется такое значение у, что х – 5 = у.
е) Существуют такие натуральные числа с и d, что с · d = 6.
ж) Для любых действительных чисел х и у существует такое действительное число z, что x 2 =121.
10.Какие из следующих высказываний равносильны конъюнкции, а какие – дизъюнкции высказываний?
а) Все студенты нашей группы присутствовали сегодня на занятиях.
б) Некоторые натуральные числа меньше 3.
в) Существуют четные числа.
г) Любой четырехугольник является квадратом.
д) Всякий параллелограмм есть ромб.
е) Найдутся треугольники, в которых одна из высот совпадает с медианой и биссектрисой.
ж) Хотя бы одно из чисел 13, 16, 21, 25, 44 является квадратом целого числа.
11.Найдите значения истинности следующих высказываний: а) Все числа множества X = <87, 89, 99, 100) двузначные. б) Каждое из множеств А = , В = , С = конечно. в) Хотя бы одно из множеств D = , Е = , F = является подмножеством множества К = . г) Некоторые из выражений 5 : 2, 5 + (7 – 8), 7: (4 – 1 – 3), 16 – (25 + 4) не имеют смысла на множестве N.
12.Известно, что высказывание ($ х Î X) А (х) истинно. Следует ли отсюда истинность высказывания («х Î X) А (х)?
13.Следует ли истинность высказывания ($ х Î X) А (х) из истинности высказывания («х Î X) А (х)?
14.Для доказательства каких из следующих утверждений необходимо провести рассуждения в общем виде, а для каких – достаточно привести пример?
а) В любом параллелограмме сумма величин противоположных углов равна 180°.
б) Найдется ромб, диагонали которого равны.
в) В некоторых треугольниках все высоты делят противоположную сторону пополам.
г) Для любого натурального числа п имеет место неравенство п 2 + 1 > 0.
д) Существуют тупоугольные треугольники.
е) Любое число, делящееся на 4, делится на 2.
15.Какие из следующих высказываний можно опровергнуть, приведя контрпример?
а) Все натуральные числа больше 2.
б) Любая фигура имеет центр симметрии.
в) Некоторые натуральные числа меньше нуля.
16.Докажите или опровергните следующие утверждения.
а) Разность любых двух натуральных чисел есть число натуральное.
б) Существуют правильные многоугольники.
в) Сумма любых трех последовательных чисел кратна 3.
г) Любое однозначное число является решением неравенства 2х – 25
| | | следующая лекция ==> | |
| Глазов 2007 | | | Практические задания |
Не нашли то, что искали? Google вам в помощь!
Видео:Множества и операции над нимиСкачать

По какому одному свойству можно разбить множество четырехугольников
КАРТА – СХЕМА УЧЕБНОГО ЗАНЯТИЯ
продолжительность – 90 минут
Тема занятия: Декартово произведение и разбиение множеств на классы
расширить знания студентов с темы действия с множествами, рассмотреть Декартово произведение, разбиение множеств на классы;
способствовать развитию памяти, внимания, логического мышления;
создать условия для применения полученных знаний при выполнении расчетных заданий.
Необходимое аппаратное и программное обеспечение:
Карточки с заданиями самостоятельной работы
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. – 4-е изд., стер. – М. : Издательский центр “Академия”, 2014.
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. – 4-е изд., стер. – М. : Издательский центр “Академия”, 2014.
Тип и вид учебного занятия:
ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА
Содержание и виды деятельности преподавателя
1. Организационный этап
Приветствие, выявление отсутствующих, информирование о теме и целях занятия.
2. Актуализация ЗУН
– Что такое множество? Что означает задать множество?
– Способы задания множеств
– Что такое подмножество?
-какие действия выполняем над множествами?
– Что такое пересечение? Объединение?
– Какие свойства пересечения, объединения?
Самостоятельная работа (с взаимопроверкой)
Найдите: а) А∩В; б) А∩С; в) С∩В.
Найдите: а) АUВ; б) АUС; в) СUВ.
Найдите а)(А∩В)∩С; б) )(АВ)С; в) (А В)∩С
3. Изучение нового материала
– разбиение множеств на классы
4. Первичное закрепление
Практическое выполнение заданий
5. Информация о домашнем задании
Методические рекомендации для самостоятельной работы
6. Подведение итогов урока
Подведение итогов работы группы, отдельных студентов.
Корректирование пробелов знаний.
В начальных классах ученики решают задачу: используя цифры 1, 2, 3 образовать всевозможные двузначные числа.
Путем перебора дети получают:
Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (а; b), образованные из элементов а и b. Это (1; 2), (1; 3), (1; 4) и т.д. Первый элемент а называют первой координатой пары, элемент b – второй.
Значит, в нашей задаче мы оперировали множеством А=<1, 2, 3> и образовывали всевозможные пары.
Рассмотрим другой пример. Пусть А=, B=. Образуем всевозможные пары (а;b) так, что аА, bВ. Получим некоторое новое множество , элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств А и В.
Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.
Рассмотрим следующий пример. Известно, что АВ= . Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству А, а вторая – множеству В, то данные множества имеют следующий вид: А=, B= <3, 5,6>.
Перечислим элементы, принадлежащие множеству АВ, если
А= <a, b, c,d>, B=A. Декартово произведение АВ=<(a, a), (a, b), (a, c),
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a), (d, b) ,(d, c), (d, d)>.
Количество пар в декартовом прoизведении АВ будет равно произведению числа элементов множества А и числа элементов множества В: n(АВ)=n(A)n(B).
В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.
Используя понятие кортежа, можно определить понятие декартового произведения n множеств.
Декартовым произведением множеств А, А,…, A называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А, вторая – А, …, n-ая – множеству А: АА…A.
Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
1) подмножества Х, Х,…, Х попарно не пересекаются;
2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
Примеры
Приведем несколько примеров разбиения:
1. Множество четырехугольников разбито на два класса:
трапеции и прямоугольники. Данные подмножества попарно не пересекаются, а их объединения совпадают с множеством .
2. Множество четырехугольников разбито на три класса:
квадраты, параллелограммы, прямоугольники. Так как прямоугольник и квадрат – частные случаи параллелограмма, то данные подмножества пересекаются, значит, не выполнено первое условие классификации, и разбиение множества не получено.
3. Дано множество прямых в пространстве, которое разбито на классы по их взаимному расположению: параллельные, пересекающиеся, скрещивающиеся. Данные подмножества попарно не пересекаются, а их объединения совпадают с множеством .
4. Дано множество , которое можно разделить на два класса: и , где – множество натуральных четных чисел, а – множество натуральных нечетных чисел.
5. Множество разбито на три класса: , и . множество чисел, которые делятся на , – множество чисел, которые делятся на , множество чисел, которые делятся на . Но существуют числа, которые могут делится одновременно и на , и . Отсюда следует, что подмножества пересекаются, и разбиение не получено.
Решение. Элементами множества А1´ А2 ´А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А1, вторая – множеству А2, третья – множеству А3.
Пример 2. Пусть на множестве Х= задано отношение «меньше» (т.е. первый элемент меньше второго, второй меньше третьего). Записать декартово произведение XX. Из этого множества следует выбрать элементы, которые должны удовлетворять отношению «меньше».
Декартово произведение X Х может быть записано в виде множества из упорядоченных пар:
Из этого множества выбираются элементы, которые удовлетворяют отношению «меньше». В результате получится новое множество из упорядоченных пар:
В новом множестве все пары являются элементами декартова произведения XX. Отношение «меньше» на множестве Х является подмножеством декартова произведения XX. Бинарное отношение на множестве Х есть подмножество декартова произведения W XX.
2) Декартово произведение двух множеств X Y.
Пусть заданы два множества: X= , Y= .
Записать декартово произведение X Y .
Декартово произведение двух множеств равно:
Аналогично можно найти декартово произведение трёх множеств: X Y Z.
Говорят, что множество Х разбито на попарно непересекающиеся подмножества или классы, если выполнены следующие условия:
1) любые два подмножества попарно не пересекаются;
2) объединение всех подмножеств совпадает с исходным множеством Х.
Разбиение множества на классы называют классификацией.
Классификацию можно выполнять при помощи свойств элементов множества.
Например, натуральные числа можно разбить на четные и нечетные. Буквы русского языка можно разбить на гласные и не гласные. Вообще, если на множестве Х задано одно свойство А, то это множество разбивается на два класса: первый класс – объекты, обладающие свойством А, второй класс – объекты, не обладающие свойством А.
Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса.
Например, на множестве натуральных чисел заданы два свойства: «быть кратным 2» и «быть кратным 3». При помощи этих свойств в множестве N можно выделить два подмножества А и В. Эти множества пересекаются, но ни одно из них не является подмножеством другого. Тогда в первый класс войдут числа, кратные 2 и 3, во второй – кратные 2, но не кратные 3, в третий – кратные 3, но не кратные 2, в четвертый – не кратные 2 и не кратные 3.
Пример 5. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:
а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;
б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?
а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.
б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.
Решите задачу используя круги Эйлера: В группе английский язык изучают 15 студентов, немецкий – 10 студентов, а французский – 5, причем 3 студента изучают одновременно английский и немецкий языки, 2 студента изучают одновременно английский и французский языки, 1 студент изучает одновременно французский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? немецкий язык? французский язык?
1. Указать какие теоретические знания были использованы в ходе выполнения работы.
2. Указать какие умения и навыки были приобретены в ходе выполнения работы.
1) Какое множество называется конечным? пустым?
2) Что называется пересечением двух множеств?
3) Что такое диаграмма Эйлера-Венна?
4) Известно, что А – множество спортсменов группы, В – множество отличников группы. Сформулируйте условия, при которых: а) А∩В=Ø б)АUВ=А.
5. РАЗБИЕНИЕ МНОЖЕСТВА НА КЛАССЫ
Можно говорить о разбиении данного множества на попарно непересекающиеся подмножества или классы тогда, когда одновременно выполняются следующие условия:
- Все подмножества, образующие разбиение, не пусты.
- Любые два таких подмножества не пересекаются.
- Объединение всех подмножеств есть данное множество. Условие 1 иногда опускают.
Символическая запись этого определения следующая.
Совокупность подмножеств А1, А2, …, Ап называется разбиением множества А на классы, а сами подмножества – классами, если выполняются условия:
Рассмотрим задачи, связанные с оценкой правильности разбиения множества на классы и с самостоятельным разбиением множества на классы при использовании двух свойств.
Учащийся из множества четырехугольников выделил подмножества трапеций, параллелограммов и прямоугольников. Произошло ли разбиение множества на классы?
Пусть А – множество четырехугольников. А1 – множество трапеций А2 – множество параллелограммов, А3 – множество прямоугольников.
Разбиение множества А на классы произойдет, если будут выполнены условия (1, 2, 3).
Проверим выполнимость условий: Аi А, где i = 1, 2, 3.
1. Аi, где i = 1, 2, 3, т.к. каждое множество содержит хотя бы по oдной фигуре.
Второе условие не выполняется, значит разбиения множества на классы не произошло.
На какие классы разбивается множество натуральных чисел, если использовать такие свойства: «делится на 2» и «быть однозначным»?
Обозначим через А множество четных натуральных чисел, В – множество однозначных чисел, N–множество натуральных чисел. Заметим, то А В , т.к. некоторые четные числа являются однозначными, а некоторые однозначные числа – четными. Далее с помощью кругов Эйлера изобразим множества А, В, Nи выделим классы разбиения. Из рисунка видим, что их 4. Охарактеризуем каждый из них.
I – множество четных однозначных натуральных чисел.
II – множество четных неоднозначных натуральных чисел.
III – множество нечетных однозначных натуральных чисел.
IV – множество нечетных неоднозначных натуральных чисел.
Упражнения
93. Из множества Р = выделили подмножества А, В и С. Выясните, в каком случае произошло разбиение множества Р на классы:
94. Множество А состоит из 3, 4, 5, 6, 7, 8, 9; множество В – его подмножество, состоящее из чисел, которые делятся на 3; множество С – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 1; множество D – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 2. Можно ли утверждать, что множество А разбивается в этом случае на попарно непересекающиеся подмножества В, С и D? Произошло ли разбиение множества на классы, если да, то сколько классов?
95. На координатной прямой выделены два множества: (–;2) и (2; +). Можно ли утверждать, что множество действительных чисел разбито на два класса? Можно ли разбить множество точек координатной прямой на 3 класса? на 4 класса? Ответ проиллюстрируйте на примере.
96. Выясните, в каких случаях классификация выполнена верно:
а) треугольники делятся на прямоугольные, тупоугольные и равнобедренные;
б) углы классифицируются на острые, прямые и развернутые;
в) целые числа можно разбить на натуральные числа, число и отрицательные целые числа;
г) глаголы русского языка делятся на глаголы настоящего, прошедшего и будущего времени;
д) члены предложения бывают главные и второстепенные.
97. Из множества Т треугольников выделили два подмножества: X– подмножество прямоугольных треугольников и Y – подмножество равнобедренных треугольников. Постройте для данных множеств круги Эйлера; установите, на сколько непересекающихся областей разбился круг, изображающий множество Т, и все множества, изображенные этими областями, задайте описанием характеристического свойства. При помощи скольких свойств произведено разбиение множества треугольников на классы?
98. Разбейте множество четырехугольников на классы: а) по какому-либо одному свойству; б) по двум свойствам. Укажите эти свойства, для каждого случая постройте круги Эйлера, установите число непересекающихся областей и выясните, какие множества изображаются этими областями.
99. Множества Р ромбов, Т треугольников и К многоугольников, имеющих угол 30°, являются подмножествами множества М многоугольников. Постройте круги Эйлера для данных множеств, установите, на сколько непересекающихся областей разбился круг, изображающий множество М, и для всех множеств, изображенных этими областями, укажите характеристическое свойство.
100. Из множества треугольников выделены подмножества прямоугольных, равнобедренных и тупоугольных треугольников. Произошло ли разбиение множества на классы?
101. Произведите разбиение на классы множества целых чисел, используя свойства «быть кратным 4» и «быть кратным 5».
102. Укажите классы разбиения множества треугольников, которые получаются при рассмотрении таких свойств, как «иметь хотя две равные стороны» и «иметь прямой угол».
103. Из множества четырехугольников выделили следующие подмножества: а) прямоугольников, не являющихся ромбами; б) ромбов не являющихся прямоугольниками; в) квадратов; г) четырехугольников, не являющихся ни ромбами, ни прямоугольника. Произошло ли разбиение множества на классы?
104. Истинно ли высказывание: «Параллелограммы делятся на прямоугольники, ромбы и квадраты»? Почему?
105. На множестве геометрических фигур плоскости выделены множества фигур, имеющих: а) центр симметрии; б) ось симметрии; в) не имеющих ни центра, ни оси симметрии. Можно ли считать, что произошло разбиение множества на классы?
106. Произведите разбиение множества целых чисел на классы используя такие свойства: «быть однозначным числом» и «быть двузначным числом».
107. Укажите, какие классы разбиения получаются при рассмотрении на множестве треугольников таких свойств: «иметь тупой угол» и «все углы острые».
108. Произошло ли разбиение множества натуральных чисел на классы, если из него выделены подмножества чисел, делящихся на три чисел, которые при делении на 3 дают остаток 1?
109. Установите, правильны ли следующие классификации:
а) натуральные числа делятся на однозначные, двузначные и трехзначные;
б) параллелограммы могут быть прямоугольниками, квадратами и ромбами;
в) треугольники бывают равносторонними и неравносторонними;
г) четырехугольники делятся на параллелограммы и трапеции.
110. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 4. Постройте круги Эйлера для множеств N, А и В; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N; укажите характеристические свойства этих множеств.
111. Из множества параллелограммов выделили подмножество прямоугольников и подмножество квадратов. Постройте круги Эйлера для данных множеств. Можно ли утверждать в данном случае, что множество параллелограммов разбито на 3 попарно непересекающихся подмножества: квадраты; прямоугольники, не являющиеся квадратами; параллелограммы, не являющиеся прямоугольниками?
6. ДЕКАРТОВО УМНОЖЕНИЕ МНОЖЕСТВ
Назовем (х, у) упорядоченной парой, а х и у – компонентами этой пары. При этом считают, что (х1 у1) = (х2.у2), если х1 = х2 и у1= у2.
__________________________________________________________________
Определение 9. Декартовым произведением множеств А и В называют множество АВ, элементами которого являются все пары(х,у), такие, что х А, уВ, т.е. АВ = .
Найдем, например, декартово произведение множеств А = <1,3> и В =.
Операцию, при помощи которой находят декартово произведение, называют декартовым умножением множеств.
Декартово умножение множеств не обладает ни свойством коммутативности, ни свойством ассоциативности, но связано с операциями объединения и вычитания множеств дистрибутивными свойствами:
для любых множеств А, В, С имеют место равенства:
Для наглядного представления декартова произведения числовых множеств часто используют прямоугольную систему координат.
Пусть А и В – числовые множества. Тогда элементами декартова произведения этих множеств будут упорядоченные пары чисел. Изобразив каждую пару чисел точкой на координатной плоскости, получим фигуру, которая и будет наглядно представлять декартово произведение множеств А и В.
Изобразим на координатной плоскости декартово произведение множеств А и В, если:
В случае а) данные множества конечны и можно перечислить элементы декартова произведения.
АВ = . Построим оси координат и на оси ОХ отметим элементы множества А, а на оси ОУ – элементы множества В. Затем изобразим каждую пару чисел множества АВ точкам на координатной плоскости (рис.7). Полученная фигура из четыре точек и будет наглядно представлять декартово произведение данных множеств А и В.
В случае б) перечислить все элементы декартова произведения множеств невозможно, т.к. множество В – бесконечное, но можно представить процесс образования этого декартова произведения: в каждой паре первая компонента либо 2, либо 6, а вторая компонента – действительное число из промежутка [1,4].
Все пары, первая компонента которых есть число 2, а вторая пробегает значение от 1 до 4 включительно, изображаются точками отрезка СД, а пары, первая компонента которых есть число 6, а вторая – любое действительное число из промежутка [1,4], – точками отрезка РS(рис.8). Таким образом, в случае б) декартово произведение множеств А и В на координатной плоскости изображается в виде отрезка СД и РS.
Рис. 7 Рис. 8 Рис. 9
Случай в) отличается от случая б) тем, что здесь бесконечно не только множество В, но и множество А, поэтому,первой компонентой пар, принадлежащих множеству А В, является любое число из промежутка [2, 6]. Точки, изображающие элементы декартова произведения множеств А и В, образуют квадрат СДЕL(рис. 9). Чтобы подчеркнуть, что элементы декартова произведения изображаются точками квадрата, его можно заштриховать.
Контрольные вопросы
- Покажите, что решение следующих задач приводит к образованию декартова произведения множеств:
а) Запишите все дроби, числителем которых является число из множества А = , а знаменателем – число из множества В = <5, 6, 7>.
б) Запишите различные двузначные числа, используя числа 1, 2, 3, 4.
- Докажите, что для любых множеств А, В, С справедливо равенство (АВ)С = (АС)(ВС). Проиллюстрируйте его выполнимость для множеств А= ,В=, С = .
- Какую фигуру образуют точки на координатной плоскости, если их координаты являются элементами декартова произведения множеств А = и В = R
- Определите, декартово произведение каких множеств А и В изображено на рисунке 10.
112. Запишите все двузначные числа, цифры десятков которых принадлежат множеству А = , а цифры единиц – множеству В = .
113. Напишите все дроби, числители которых выбираются из множества А= <3, 5, 7>, а знаменатель – из множества В= .
114. Напишите все правильные дроби, числители которых выбираются из множества А = , а знаменатель – из множества В= <4, 6,8>.
116.Известно, что АВ = . Установите, из каких элементов состоят множества А и В.
119. Известно, что АВ = . Установите, из каких элементов состоят множества А и В.
120. Найдите декартово произведение множеств А = и В = и выделите из него подмножество пар, в которых:
а) первая компонента больше второй; б) первая компонента равна 5; в) вторая компонента равна 7.
121. Перечислите элементы, принадлежащие декартову произведению множеств А, В и С, если:
122. Изобразите на координатной плоскости элементы декартова про
изведения множеств А и В, если:
123. Все элементы декартова произведения двух множеств A и B изображены точками в прямоугольной системе координат. Запишите множества A и В (рис. 11).
124. Изобразите на координатной плоскости элементы декартова произведения множеств X и Y, если:
125. Фигуры, приведенные на рис. 14, являются результатом изображения на координатной плоскости декартова произведения множеств X и Y. Укажите для каждой фигуры эти множества.
126. Выясните, декартово произведение каких двух множеств изображается на координатной плоскости в виде полуплоскости. Рассмотрите все случаи.
127. Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде прямого угла, который образуется при пересечении координатных осей.
128. На координатной плоскости постройте прямую, параллельную оси ОХ и проходящую через точку Р (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.
129. На координатной плоскости постройте прямую, параллельную оси ОY и проходящую через точку Р (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.
130. На координатной плоскости постройте полосу, ограниченную прямыми, проходящими через точки (–2, 0) и (2, 0) и параллельными оси ОY. Опишите множество точек, принадлежащих этой полосе.
131. На координатной плоскости постройте прямоугольник, вершинами которого служат точки А (–3, 5), В (–3, 8), С (7, 5), D(7, 8). Опишите множество точек этого прямоугольника.
132. Постройте на координатной плоскости множество точек, координаты которых удовлетворяют условию:
Видео:Разбиение множества на классыСкачать

Разбиение множества на классы
Два множества, содержащих одинаковые элементы, называются пересекающимися. В этом случае говорят, что множества пересекаются.
Два множества, нс имеющих общих элементов, называются непересекающимися. В этом случае говорят, что множества не пересекаются.
Пример 6.3.1. Множества , нс псрссскаются.
Непересекающимися являются множество треугольников и множество параллелограммов.
Также нс псрссскаются множества решений уравнений * 3 =3* 2 и *+3=0. •
Пример 6.3.2. Пусть А — множество треугольников, площадь которых равна 6, В — множество прямоугольных треугольников.
А и В — пересекающиеся множества, так как существует треугольник, являющийся одновременно элементом множеств А и В, например треугольник со сторонами 3, 4, 5. Он прямоугольный и имеет площадь.
равную 6 (проверьте эти утверждения). Этот пример нс единственен. Приведите пример еще одного такого треугольника.
Пересекаются также множества решений уравнений х 2 +х=0 и х 2 -х=0, так как оба эти множества содержат число 0. •
Заметим, термины «множества пересекаются» и «множества не пересекаются» определены для двух множеств. Если множеств будет больше, то необходимы уточнения. Например, множества могут нс иметь ни одного общего элемента, но некоторые из множеств могут пересекаться.
Пример 6.3.3. Множества , и не пересекаются в совокупности, то есть нет ни одного элемента, который принадлежал бы каждому из множеств. Однако любая пара этих множеств имеет общий элемент. •
Пусть дана совокупность множеств. Говорят, что множества этой совокупности попарно не пересекаются, если никакие два (различных) множества совокупности нс псрссскаются.
Пример 6.3.4. Множества , , и попарно не пересекаются. •
Два множества могут находиться в следующих отношениях:
- 1) множества могут быть пересекающимися,
- 2) множества могут быть нспсрссскающимися,
- 3) множества могут быть связаны отношением включения.
Ясно, что первые два отношения исключают друг друга, то есть каждое из предложений «Множества псрссскаются» и «Множества нс псрссскаются» является отрицанием другого. Пересекающиеся множества, в частности, могут быть связаны отношением включения. На первый взгляд может показаться, что нспсрссскающисся множества не могут находиться в отношении включения. Это так, но только с некоторым исключением.
Пример 6.3.5. Рассмотрим два предложения:
Р = «Множества А и В пересекаются»,
Q = «Множество А содержится в множестве В».
Ясно, что РФ(). Оказывается, обратное утверждение в общем случае тоже неверно, то есть ()ФР. Контрпример: Л=0, В — любое. Как известно, 0сЯ, но это непересекающиеся множества.
🎬 Видео
Пересечение множеств. Объединение множеств. 5 класс.Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Алгебра 8 класс (Урок№38 - Множества чисел.)Скачать

95 Разбиение множества на классы эквивалентностиСкачать

Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Множество. Элементы множества. 5 класс.Скачать

Свойства арифметического квадратного корня. 8 класс.Скачать

Множества. Операции над множествами. 10 класс алгебраСкачать

9 класс, 2 урок, Множества и операции над нимиСкачать

Операции над множествамиСкачать

Отношение эквивалентности как разбиение множестваСкачать

Пересечение и объединение множеств. Алгебра, 8 классСкачать

Степень с натуральным показателем. Свойства степеней. 7 класс.Скачать

Математика это не ИсламСкачать

ПОДМНОЖЕСТВА. Операции над множества. §14 алгебра 8 классСкачать

Математика. 3 класс. Множества. ПодмножестваСкачать

Числовые множества, 6 классСкачать

Математика 2 класс. «Множества и операции над ними»Скачать











