Как повернуть один вектор в другой

Структура публикации

• Получение кватерниона из вектора и величины угла разворота
• Обратный кватернион
• Умножение кватернионов
• Поворот вектора
• Рысканье, тангаж, крен
• Серия поворотов

Получение кватерниона из вектора и величины угла разворота

Ещё раз – что такое кватернион? Для разработчика – это прежде всего инструмент, описывающий действие – поворот вокруг оси на заданный угол:

где v – ось, выраженная вектором;
w – компонента, описывающая поворот (косинус половины угла).

Положительное значение угла разворота означает поворот вдоль вектора по часовой стрелке, если смотреть с конца вектора в его начало.

Например, кватернион поворота вдоль оси Х на 90 градусов имеет следующие значения своих компонент: w = 0,7071; x = 0,7071; y = 0; z = 0. Левая или правая система координат, разницы нет – главное, чтобы все операции выполнялись в одинаковых системах координат, или все в левых или все в правых.

С помощью следующего кода (под рукой был Visual Basic), мы можем получить кватернион из вектора и угла разворота вокруг него:

В коде rotate_vector – это вектор, описывающий ось разворота, а rotate_angle – это угол разворота в радианах. Вектор должен быть нормализован. То есть его длина должа быть равна 1.

Не забывайте про ситуацию, когда длина может быть 0. Вместо ошибки вам может понадобиться обработать эту ситуацию индивидуально.

Обратный кватернион

Для поворота вектора кватернионом требуется уметь делать обратный разворот и правильно выполнять операцию умножения кватернионов. Под обратным разворотом я имею ввиду обратный кватернион, т. е. тот, который вращает в обратную сторону.

Чтобы получить обратный кватернион от заданного, достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион. Нормализация кватерниона так же как и в векторах, это просто приведение к длине = 1.

Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0). Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 градусов она = 0. Кватернион, который означает «нет разворота» = (w=1; x = 0; y = 0; z=0), то есть у него длина вектора оси = 0.

Умножение кватернионов

Умножение кватернионов крайне полезная штука. Результатом умножения является кватернион, который после поворота даёт такой же результат, если последовательно выполнить развороты умножаемыми кватернионами. Причём разворот будет происходить в локальной для поворачиваемого вектора системе отчёта, т. е. система отчёта поворачиваемого вектора также двигается.

Умножение кватернионов выполняется следующим образом:

Для того, чтобы умножить кватернион на 3D вектор, нужно вектор преобразовать в кватернион присвоив компоненте W = 0 и умножить кватернион на кватернион. Или подставить ноль и выразить это в виде функции:

Поворот вектора

Теперь, собственно, поворот вектора кватернионом:

Вектор описывающий ось (x=1; y=0; z=1). Угол поворота 180 градусов.
Поворачиваемый вектор (x=0; y=0; z=1). Результат равен (x=1; y=0; z=0).

Рысканье, тангаж, крен

Рассмотрим инструмент формирования кватерниона с помощью поворотов вокруг одной из осей:
Рысканье = heading = yaw = вокруг оси Z; тангаж = altitude = pitch = вокруг оси Y; крен = bank = roll = вокруг оси X.

И в обратную сторону, из кватерниона:

Формулы преобразования зависят от принятой системы координат.

Серия поворотов

Рассмотрим пример:
1. Первый поворот – рысканье (вокруг Z) 90 градусов по часовой;
2. Второй поворот – тангаж (вокруг Y) 90 градусов по часовой;
3. Третий поворот – крен (вокруг X) 90 градусов по часовой.

Рисунки, изображающие поворот и подписанные как «global» демонстрируют повороты относительно неподвижных осей XYZ. Такой результат мы получим, если будем использовать кватернионы разворота по отдельности. Четвёртый рисунок демонстрирует, где окажется вектор, если начальные координаты у него были X=1; Y=0; Z=0.

Рисунки, подписанные как «local» демонстрируют вращение осей вместе с самолетом. То есть все вращения происходят относительно пилота, а не относительно неподвижной системы координат. Четвёртый рисунок показывает, где окажется тот же самый вектор (1; 0; 0) в итоге всех трёх поворотов. Такой результат мы получим, перемножив кватернионы разворота и применив полученный кватернион.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Как перевернуть вектор в C++?

Если вектор имеет элементы в последовательности, , и он переконфигурируется так, что его последовательность становится, , то вектор был перевернут. К сожалению, в C ++ такая прямая обратимость невозможна. Однако вектор в C ++ может повторяться сзади, и это косвенная обратимость. При этом нет необходимости буквально переворачивать вектор. В этой статье объясняется, как выполнить итерацию вектора в C ++ с обратной стороны и изменить его элементы.

Перед использованием вектора в C ++ программа должна начинаться с,

с включенной векторной библиотекой. Обратную итерацию легче понять, если составить сводку пересылки итерации. Таким образом, перед объяснением обратной итерации сначала резюмируется прямая итерация.

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Прямая итерация

Прямая итерация имеет дело с двумя итераторами. Итератор — это тщательно продуманный объект-указатель со специальными характеристиками. Здесь два интересующих нас итератора возвращаются функцией-членом begin () и функцией-членом end (). Функция-член begin () возвращает итератор, указывающий на первый элемент вектора. Функция-член end () возвращает итератор, который указывает сразу за последним элементом вектора.

Предположим, что имя вектора — vtr, тогда следующий оператор вернет начальный итератор:

где p — имя начального итератора. Следующий оператор вернет конечный итератор:

где q — это имя, данное конечному итератору, из двух приведенных выше операторов видно, что p и q имеют один и тот же тип и даже могут быть заменены местами.

Все фрагменты кода для этой статьи написаны в функции main (). Следующий код считывает все элементы вектора от начала до последнего:

for ( vector char > :: iterator p = vtr. begin ( ) ; p ! = vtr. end ( ) ; p ++ ) <
cout * p ‘ ‘ ;
>
cout vtr = ;

vector char > :: iterator q = vtr. end ( ) ;
for ( q = — q ; q >= vtr. begin ( ) ; q — ) <
cout * q ‘ ‘ ;
>
cout endl ;

Код в круглых скобках цикла for требует пояснения. p — итератор, который сначала указывает на первый элемент вектора. Хотя он еще не указывает только за пределы вектора, он увеличивается на p ++, чтобы указать на каждый элемент в векторе. Когда он указывает на элемент в векторе, значение (символ) элемента получается с помощью * p в теле цикла for. * — косвенный оператор.

Следующий код считывает и отображает значения в векторе от последнего элемента до первого элемента, используя конечный итератор:

vector char > :: iterator q = vtr. end ( ) ;
for ( q = — q ; q >= vtr. begin ( ) ; q — ) <
cout * q ‘ ‘ ;
>
cout endl ;

Конечный итератор указывает сразу за концом вектора, и это не элемент. Таким образом, он должен быть сначала уменьшен, прежде чем он сможет указывать на последний элемент. Оттуда итерация может идти назад.

Условие while для цикла for здесь: «если q больше или равно начальному итератору». Не может быть «если q не равно начальному итератору», так как это исключит первый элемент.

Это неформальный способ итерации в обратном направлении. То есть это неформальный способ косвенного обращения вектора.

Видео:Найдите разложение вектора по векторам (базису)Скачать

Изменение значения элемента

Когда экземпляру вектора не предшествует const (для константы), значение любого элемента в векторе может быть изменено. Следующий код иллюстрирует это:

vector char > :: iterator q = vtr. end ( ) ;
q — ; q — ; q — ;

vector char > :: iterator r = vtr. end ( ) ;
for ( r = — r ; r >= vtr. begin ( ) ; r — ) <
cout * r ‘ ‘ ;
>
cout endl ;

Конечный итератор q уменьшается три раза на «q—; q—; q—; » указать на «C».

Если экземпляру вектора предшествует константа, то значение элемента не может быть изменено. В этом случае постоянный прямой итератор должен быть возвращен для конечного или начального итератора. Следующий код не будет компилироваться, потому что сделана попытка изменить значение ’C’:

vector char > :: const_iterator q = vtr. end ( ) ;
q — ; q — ; q — ;

Видео:Как разложить вектор по базису - bezbotvyСкачать

Обратная итерация

У обратной итерации есть два основных итератора. Эти итераторы возвращаются функциями-членами rbegin () и rend (). rend () возвращает итератор, который указывает прямо перед первым элементом вектора. rbegin () возвращает итератор, указывающий на последний элемент вектора. Следующий код считывает и отображает элементы вектора от первого до последнего в прямом направлении:

vector char >> : reverse_iterator p = vtr. rend ( ) ;

for ( p = — p ; p >= vtr. rbegin ( ) ; p — ) <
cout * p ‘ ‘ ;
>
cout endl ;

Используется обратный итератор. Поскольку rend () возвращает итератор, который указывает прямо перед первым элементом, который не является элементом, его необходимо увеличить, чтобы указать на первый элемент. Поскольку мы имеем дело с обратным итератором, оператор приращения здесь — а не ++. Кроме того, в условии while> = используется вместо char > vtr = ;

for ( vector char > :: reverse_iterator q = vtr. rbegin ( ) ; q vtr. rend ( ) ; q ++ ) <
cout * q ‘ ‘ ;
>
cout endl ;

Функция-член rbegin () возвращает итератор, указывающий на последний элемент вектора. Возвращенный итератор — это reverse_iterator. rend () возвращает итератор, который указывает непосредственно перед первым элементом. Обратите внимание, что условие while для цикла for имеет but =, поскольку мы имеем дело с обратным итератором. Уменьшение с помощью этого итератора — ++, а не -.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Изменение значения элемента

Когда экземпляру вектора не предшествует const (для константы), значение любого элемента в векторе может быть изменено с помощью reverse_iterator. Следующий код иллюстрирует это с помощью reverse_iterator:

vector char > :: reverse_iterator q = vtr. rbegin ( ) ;
q ++ ; q ++ ;

for ( vector char > :: reverse_iterator r = vtr. rbegin ( ) ; r vtr. rend ( ) ; r ++ ) <
cout * r ‘ ‘ ;
>
cout endl ;

Итератор rbegin (), q уменьшается два раза на «q ++; q ++; » чтобы указать на ’C’, поскольку он изначально указывает на последний элемент.

Если экземпляру вектора предшествует const, то никакое значение элемента не может быть изменено с помощью итератора, будь то итератор reverse_iterator (или вперед). В этом случае постоянный обратный итератор должен быть возвращен для функции rbegin () или rend (). Следующий код не будет компилироваться, потому что сделана попытка изменить значение ’C’:

vector char > :: const_reverse_iterator q = vtr. rbegin ( ) ;
q ++ ; q ++ ;

Видео:Единичный векторСкачать

Постоянный обратный итератор

crbegin () ведет себя как rbegin (), но возвращает const_reverse_iterator независимо от того, было ли создание экземпляра вектора начато с const. Это означает, что значение возвращенного итератора изменить нельзя. crend ​​() ведет себя как rend (), но возвращает const_reverse_iterator независимо от того, было ли создание экземпляра вектора начато с const. Это означает, что значение возвращенного итератора изменить нельзя.

Следующий код отображает все значения вектора, используя const_reverse_iterator, начиная с последнего элемента:

for ( vector char > :: const_reverse_iterator q = vtr. crbegin ( ) ; q vtr. crend ( ) ; q ++ ) <
cout * q ‘ ‘ ;
>
cout endl ;

Следующий код не будет компилироваться, потому что здесь мы имеем дело с постоянным обратным итератором. Создание экземпляра вектора не предшествует const.

for ( vector char > :: reverse_iterator q = vtr. rbegin ( ) ; q vtr. rend ( ) ; q ++ ) <
cout * q ‘ ‘ ;
>
cout endl ;

Видео:№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Заключение

Вектор нельзя поменять местами буквально. Однако его можно повторять от начала до конца, чтобы получить аналогичный результат. При прямой итерации задействованы функции-члены begin () и end (). В случае обратной итерации задействуются функции-члены, rbegin () и rend (). В этом случае задействованный итератор — это reverse_iterator, а не итератор. Тем не менее, в этом случае ++ — это -, а> = — это

Видео:Проекция вектора на вектор.Скачать

Как найти правильное вращение от одного вектора к другому?

У меня есть два объекта, и у каждого объекта есть два вектора:

• нормальный вектор
• вверх вектор

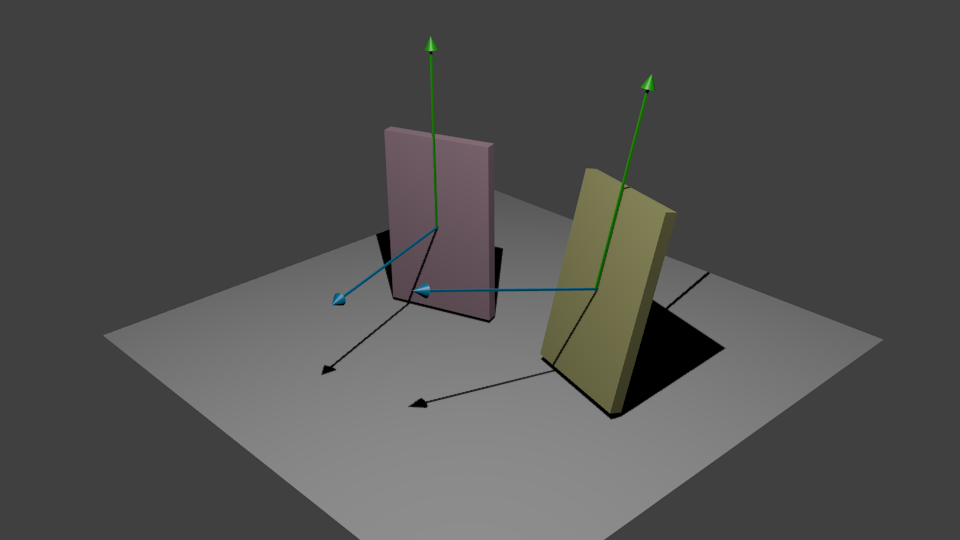
Как на этом изображении:

Вверх вектор перпендикулярен нормальному вектору. Теперь я хочу найти уникальное вращение от одного объекта к другому, как это сделать?

У меня есть один метод, чтобы найти вращение между одним вектором к другому, и это работает. Проблема в том, что мне нужно позаботиться о двух векторах: нормальный вектор и вектор вверх. Если я использую этот метод для поворота вектора нормали от объекта один к объекту нормали от объекта два, вектор вверх может указывать неправильный путь, и они должны быть параллельны.

Вот код для поиска кратчайшего поворота:

Что я должен изменить / добавить в этот код, чтобы найти правильный поворот?

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Решение

Прежде чем мы начнем, я предполагаю, что и вектор UP, и вектор нормали нормированный а также ортогональный (точка продукта равна нулю) между ними.

Допустим, вы хотите повернуть свою желтую пластину, чтобы она совпала с розовой (красной?) Пластиной. Таким образом, нашей ссылкой будут векторы из желтой пластины, и мы будем называть нашу систему координат XYZ, где Z -> нормальный желтый вектор, Y -> верхний желтый вектор и X -> YxZ (перекрестное произведение).

Таким же образом, для пластины розы повернутая система координат будет называться X’Y’Z ‘, где Z’ -> вектор нормальной розы, Y ‘-> вектор восходящей розы и X’ -> Y’xZ ‘(перекрестное произведение ).

Хорошо, чтобы найти матрицу вращения, нам нужно только убедиться, что наш нормальный желтый вектор станет вектором нормальной розы; что наш верхний желтый вектор будет преобразован в вектор восходящей розы и т. д., т.е.

другими словами, после того, как у вас есть какие-либо примитивы, преобразованные в координаты желтой системы, применяя это преобразование, поверните его, чтобы выровнять с системой координат розы.

Если ваш верхний и нормальный вектор не являются ортогональными, вы можете легко исправить один из них. Просто сделайте перекрестное произведение между нормальным и верхним значениями (для удобства получается вектор с именем C) и повторите перекрестное произведение между C и нормальным, чтобы исправить вектор повышения.

Видео:Вычитание векторов. 9 класс.Скачать

Другие решения

Код кватерниона вращает только один вектор в другой без вектора «вверх».

В вашем случае просто построить матрицу вращения из 3 ортогональных векторов

1. нормализованный (единичный) вектор направления
2. нормализованный вектор
3. перекрестное произведение векторов направления и вверх.

Тогда у вас будет матрица R1 и R2 (3×3), представляющая вращение объекта в двух случаях.

Чтобы найти вращение от R1 до R2, просто сделайте

И матрица R1_to_R2 является матрицей преобразования из одной ориентации в другую. ПРИМЕЧАНИЕ: R1.inversed () здесь можно заменить на R1.transposed ()

Позвольте мне снова написать задачу, используя векторы, которые есть у вас на рисунке.

Проблема:

Допустим, у вас есть два вектора, blue_1 а также green_1 (они ортогональны), и вы ищете вращение, чтобы переместить эти векторы в blue_2 а также green_2 (они ортогональны). Более того, вы хотите green_2 быть параллельным green_1 ,

Решение:

Как я вижу, проблема здесь в том, что эти вращения существуют только в определенных ситуациях. Ваш вектор blue_2 должно быть уже ортогонально green_1 , Если blue_2 не ортогонально green_1 ваше вращение не существует.

Зачем?

Позволяет R быть вращением, то есть,

Мы знаем, что green_2 ортогонален blue_2, поэтому

Также green_2 и green_1 будут параллельными, только если они равны постоянному коэффициенту, отличному от нуля, скажем, a это реальное число.

Собрав все воедино, вы получите это

потому что не ноль, мы получаем, что

Пример:

если ваши векторы

и ваш новый вектор синий

blue_2 = (sqrt (2) / 2, sqrt (2) / 2,0)

тогда нет вероятности того, что вектор green_2 удовлетворяющие вашей ортогональности существуют, и тогда вы не найдете вращение, которое движется blue_1 но нет green_1 ,

Прежде всего, я утверждаю, что существует только одно такое преобразование, которое выровняет ориентацию двух объектов. Поэтому нам не нужно беспокоиться о поиске самого короткого.

Пусть объект, который будет вращаться, будет назван a и назовите объект, который остается неподвижным b , Позволять x а также y быть нормальными и восходящими векторами соответственно для a и так же пусть u а также v быть эти векторы для b , Я приду x , y , u , а также v единица длины, и это x ортогонально y , а также u ортогонально v , Если что-то из этого не так, может быть написан код дела, чтобы исправить это (посредством планарной проекции и нормализации).

Теперь давайте построим матрицы, определяющие «мировое пространство» ориентацию a а также b , (позволять ^ обозначим перекрестное произведение) построить z как x ^ y и построить c как a ^ b , Пишу x , y , z а также a , b , c чтобы столбцы каждой матрицы давали нам две матрицы, назовите их A а также B соответственно. (перекрестное произведение здесь дает нам единичную длину и взаимно ортогональный вектор, поскольку то же самое верно для операндов)

Изменение преобразования системы координат для получения B с точки зрения A является A^-1 (обратная матрица A , где ^ обозначает обобщение показателя степени), в данном случае A^-1 может быть вычислено как A^T Позади, так как A является ортогональной матрицей по построению. Затем физическое преобразование в B это просто матрица B сам. Таким образом, преобразование объекта A^-1 а затем B даст желаемый результат. Однако эти преобразования могут быть объединены в одно преобразование путем умножения B справа в A^-1 налево.

В итоге вы получите эту матрицу (при условии отсутствия арифметических ошибок):

🌟 Видео

Самопересекающиеся вектора в ArtCam. Как их победить?Скачать

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Как притягивать внимание окружающихСкачать

Разложить вектор m по векторам a,b,cСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Линейная зависимость векторовСкачать

Коллинеарные вектораСкачать

Математика это не ИсламСкачать