Как найти высоту в правильном четырехугольнике

Одной из объемных фигур, изучаемых в курсе пространственной геометрии, является пирамида. Важной характеристикой этой фигуры является ее высота. В статье дадим определение высоты пирамиды и приведем формулы, через которые она связана с другими линейными характеристиками.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Что собой представляет пирамида

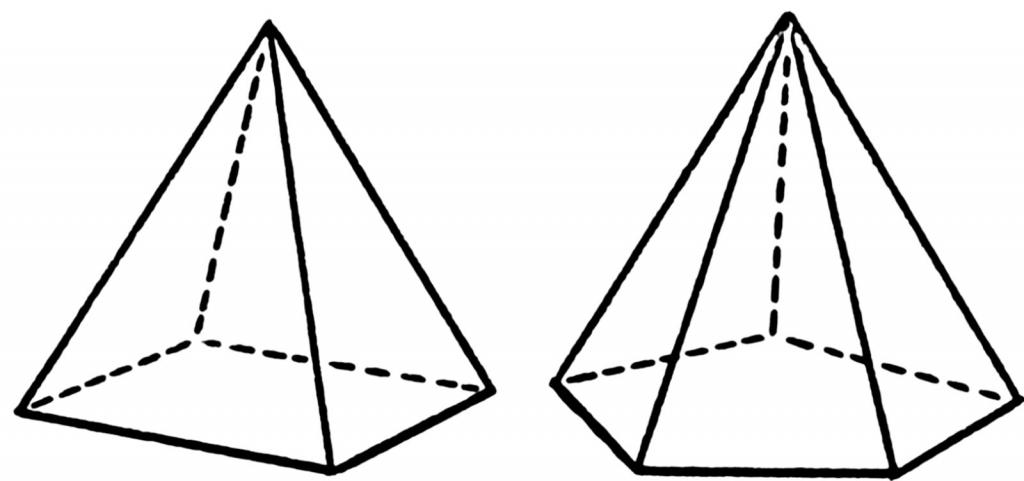
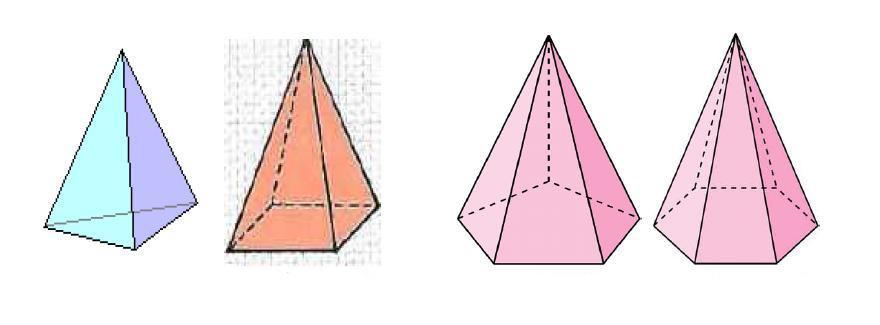
Под пирамидой понимают геометрическую фигуру пространственную, которая получается в результате соединения всех углов многоугольника с одной точкой пространства. Рисунок ниже демонстрирует расположение линий (ребер) для четырехугольной и пятиугольной пирамид.

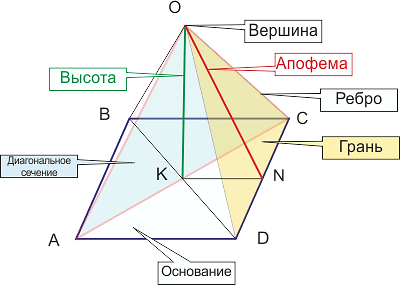
Многоугольная грань фигуры называется ее основанием. Точка, где все треугольные грани соединяются, называется вершиной. Для определения высоты пирамиды отмеченные элементы являются важными.

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Высота фигуры

Высотой пирамиды называется перпендикуляр, который из ее вершины опущен на плоскость основания. Важно понимать, что из каждой вершины, принадлежащей основанию фигуры, тоже можно провести перпендикуляр к соответствующей треугольной грани, однако он высотой не будет являться. Высота пирамиды — это единственный перпендикуляр, который является одной из важных ее линейных характеристик.

Каждому школьнику известно, что любая плоская фигура обладает геометрическим центром (в физике ему соответствует центр масс). Например, геометрический центр для произвольного треугольника определяется точкой пересечения его медиан, для параллелограмма — точкой пересечения диагоналей. Если высота пирамиды пересекает ее основание в геометрическом центре, то фигура называется прямой. Пирамида прямая, имеющая в основании многоугольник с одинаковыми сторонами и углами, называется правильной.

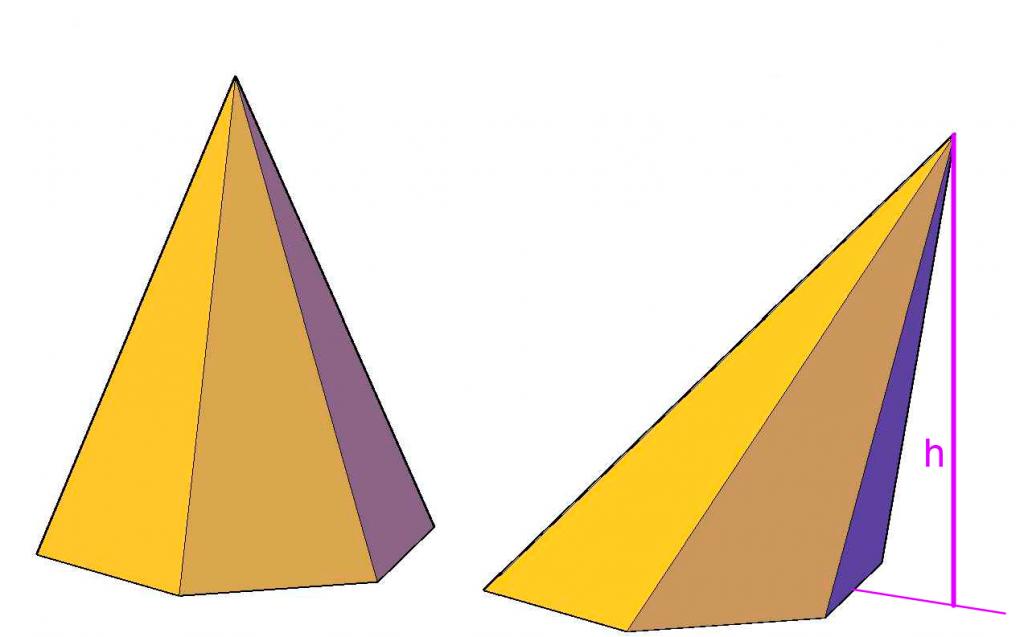
Рисунок выше показывает, чем отличается неправильная пирамида от правильной. Видно, что высота неправильной фигуры лежит за пределами ее основания, в то время как у правильной шестиугольной пирамиды высота находится внутри фигуры, пересекая ее основание в центре геометрическом.

Важными свойствами всех правильных пирамид являются следующие:

• все боковые грани представляют собой равнобедренные треугольники и равны друг другу;
• длины боковых ребер и апофем являются одинаковыми.

Видео:Нахождение высоты в правильной пирамидеСкачать

Формулы для высоты правильной пирамиды

Существует четыре основных линейных характеристики для любой пирамиды правильной:

• сторона основания;
• боковое ребро;
• апофема боковой грани;
• высота фигуры.

Все они связаны математически друг с другом. Обозначим длину стороны основания символом a, высоту — h, апофему — h_b и ребро — b. Формулы, которые эти величины связывают, имеют индивидуальный вид для соответствующей n-угольной пирамиды. Например, для правильной пирамиды четырехугольной высоту можно определить по формулам:

Эти формулы следуют из теоремы Пифагора при рассмотрении соответствующих прямоугольных треугольников внутри пирамиды.

Если рассматривается фигура с треугольным основанием, тогда справедливы следующие формулы для высоты правильной пирамиды:

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Решение задачи с шестиугольной пирамидой

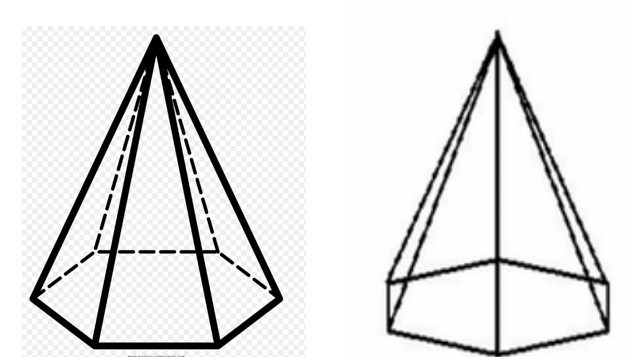
Предположим, что нам дана пирамида правильная с шестиугольным основанием. Известно, что высота основания пирамиды равна 13 см. Зная, что длина ее бокового ребра равна 10 см, необходимо вычислить объем и высоту правильной шестиугольной пирамиды.

Рисунок ниже показывает, как выглядит правильный шестиугольник.

Расстояние между любыми его двумя параллельными сторонами называется высотой. Не сложно показать, что эта высота h_a связана с длиной стороны фигуры следующей формулой:

Подставляя в выражение значение h_a, находим, что сторона основания a равна 7,51 см.

Высоту h фигуры можно определить, если рассмотреть прямоугольный треугольник, находящийся внутри пирамиды и состоящий из двух катетов (высота пирамиды и половина диагонали шестиугольного основания) и гипотенузы (боковое ребро). Тогда значение h будет равно:

Объем пирамиды определяется как третья часть от произведения высоты фигуры на площадь ее основания. Площадь правильного шестиугольника равна:

S₆ = n/4*a 2 *ctg(pi/n) = 6/4*a 2 *ctg(pi/6) = 3*√3/2*a 2 = 3*√3/2*56,4 ≈ 146,53 см 2 .

Использованная для вычисления S₆ формула является универсальной для произвольного правильного n-угольника.

Для определения объема фигуры остается подставить в соответствующую формулу найденные параметры:

Мы получили значение высоты пирамиды и рассчитали ее объем. Таким образом, поставленная задача решена.

Видео:Задача на нахождение высоты параллелограммаСкачать

Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида

Когда человек слышит слово «пирамида», то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Что такое пирамида в общем случае?

В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

Мы видим что первая фигура имеет треугольное основание, вторая — четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

• в основании должен находиться правильный многоугольник;
• боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Правильная четырехугольная пирамида

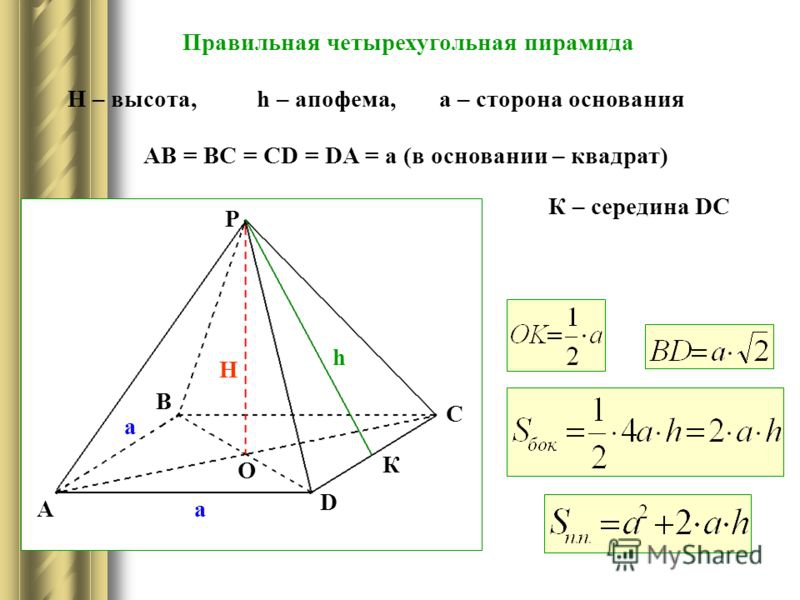
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Видео:Как разметить фундамент / Быстрая и точная разметка / Способ на раз,два,три /диагональ фундамента /Скачать

Площадь и объем фигуры

Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

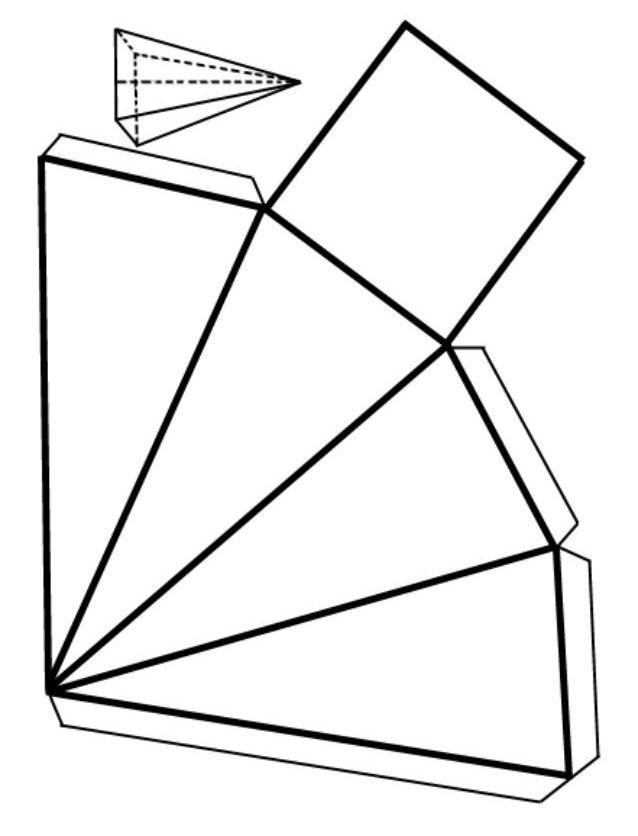
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

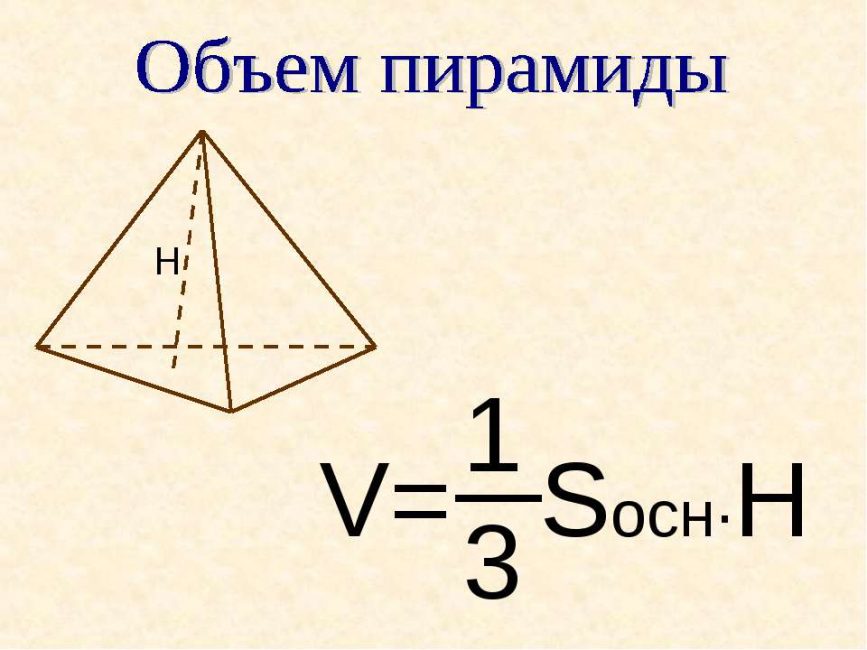
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Свойства правильной усеченной четырехугольной пирамиды

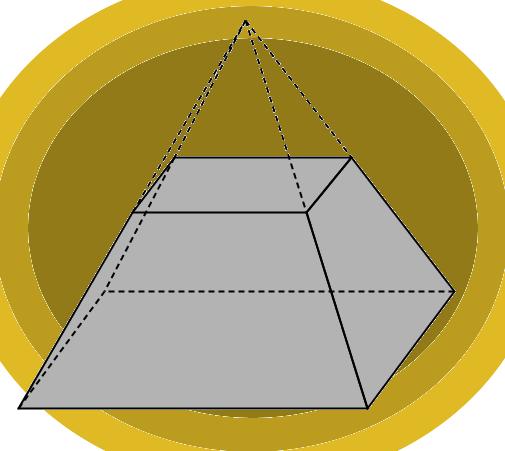
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание — это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Здесь h — расстояние между основаниями фигуры, So1, So2 — площади нижнего и верхнего оснований.

Видео:How to properly file rafters in a hip roof./ Как правильно запиливать стропила в вальмовой крыше.Скачать

Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.

В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.

Содержание этой статьи:

Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Теория

Правильная пирамида

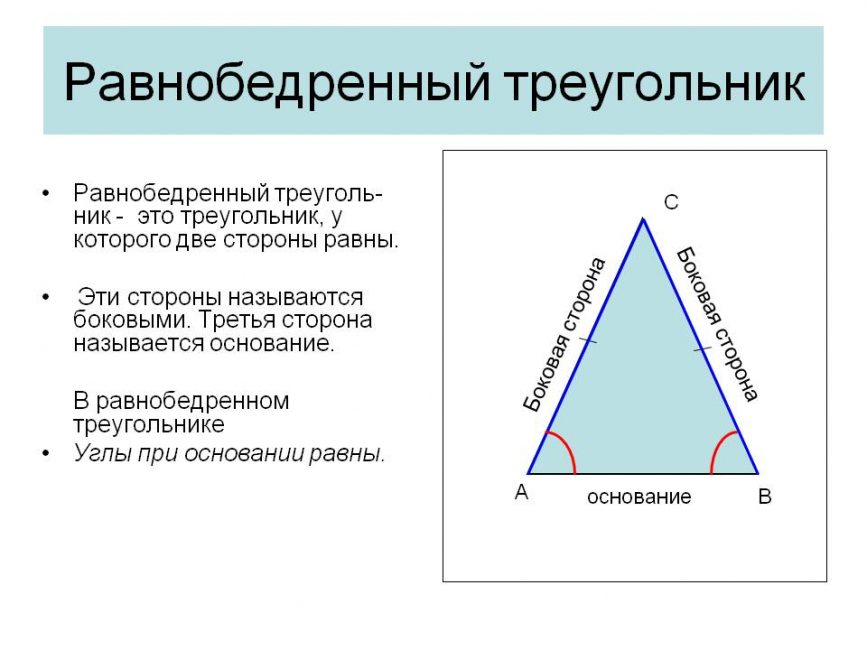
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.

Для решения задач понадобится знать теоремы равнобедренного треугольника:

Основные свойства

Четырехугольная пирамида

В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

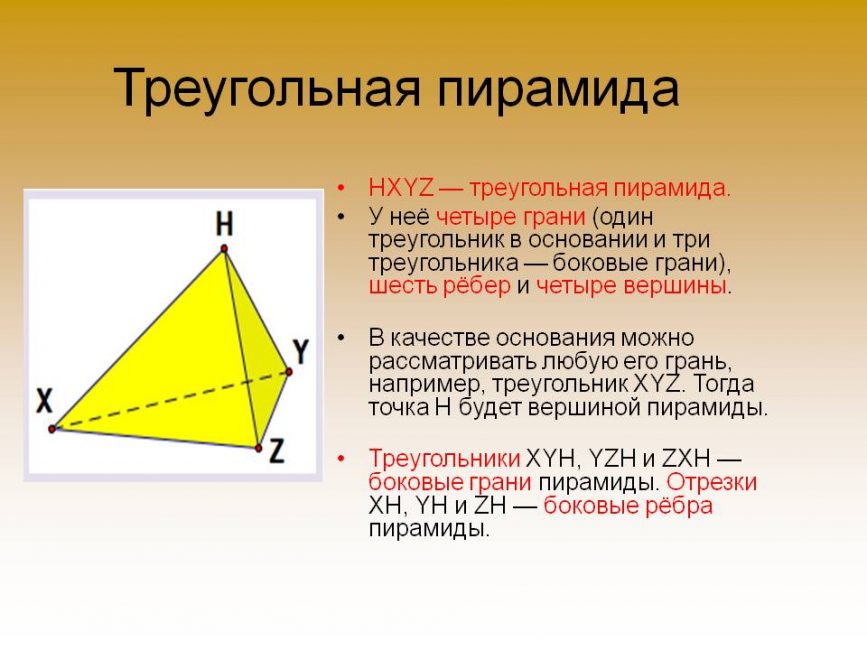
Треугольная пирамида

В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

Необходимые знания для нахождения высоты

Когда теория закреплена, можно переходить к формулам.

Формулы для нахождения высоты

Запомните, что маленькая буква h – это апофема, а большая H – высота.

В некоторых задачах, высоту можно найти через объем:

ВИДЕО: Примеры решения задач

Нахождение высоты в правильной пирамиде

Нахождение высоты в правильной пирамиде

Ниже будут представлены текстовые решения часто встречающихся задач.

Треугольная пирамида

Задача 1

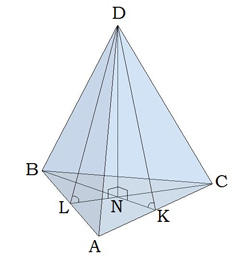
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.

DN – высота, следовательно, объем фигуры можно выразить по формуле:

DN = 3V/S основания = 3*12/4 = 9

Задача 2

DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.

Пользуясь формулой объема, получается:

DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6

Четырехугольная пирамида

Задача 1

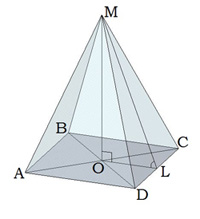
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.

ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:

Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:

MO ² = √ML ² — √OL ² = √100- √36 = √64

Задача 2

Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.

Найдем OL

В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).

Пользуясь теоремой Пифагора, находим OL:

OL² = √OC² — √LC² = √100 – √36 = √64 = 8

Задача 3

Ищем MO

Пользуясь той же теоремой, находим высоту:

MO² = √ML² – √OL² = 100 – 64 = 36

Задача 4

Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.

Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.

Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.

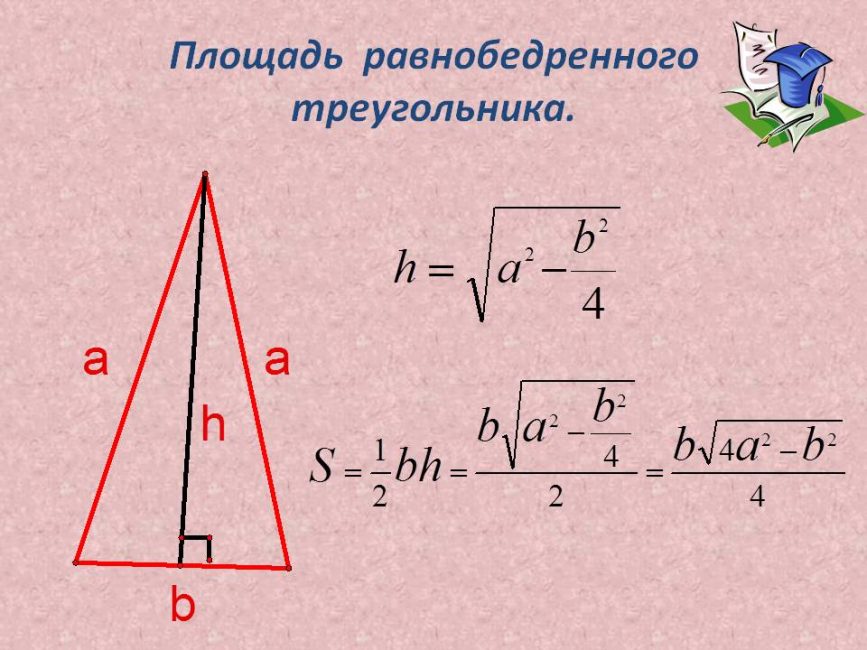
Площадь равнобедренного треугольника

Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.

MO = ML – OL = 18 – 6 = 12

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Часто задаваемые вопросы

Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.

Зная определения и свойства, определить тип фигуры очень легко.

Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.

Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.

Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.

Если выразить высоту через формулу объема, то получится следующее:

Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²

Видео:Разметка участка под постройку своими рукамиСкачать

Типичные ошибки на ЕГЭ

Видео:Нахождение высоты правильной четырехугольной пирамидыСкачать

Полезные советы

• Если в задаче указан объем – ищите высоту через него.
• Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
• Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
• Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
• Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.

Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи! Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!

📽️ Видео

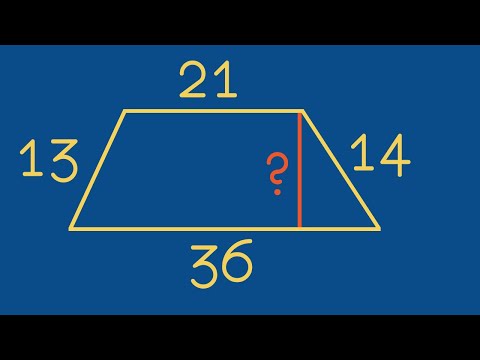
Как найти высоту трапеции, зная все стороны?Скачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

как найти высоту крыши и длину стропило по углу наклонаСкачать