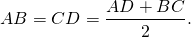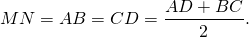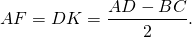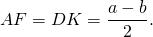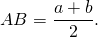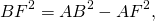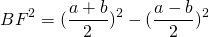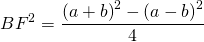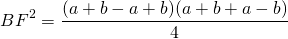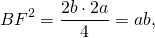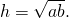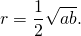Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники 
и 
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия – 
Отношение площадей этих треугольников есть 
.
4. Треугольники 
и 
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:Задача про трапецию, описанную около окружностиСкачать
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Окружность, вписанная в трапециюСкачать
Вписанная окружность
Если в трапецию вписана окружность с радиусом 
и она делит боковую сторону точкой касания на два отрезка — 
и 
, то 
Видео:Вписанная и описанная трапеции. КлассикаСкачать
Площадь
или 
где 
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Трапеция и вписанная окружностьСкачать
Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
По свойству равнобедренной трапеции,
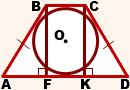
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
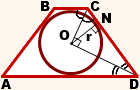
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
Окружность вписанная в трапецию касается оснований в их серединах
Вопрос по математике:
Доказать, что окружность, вписанная в равнобокую трапецию, касается оснований в их серединах.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
🎬 Видео
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
ОГЭ ЗАДАНИЕ 16 РАДИУС ОКРУЖНОСТИ ВПИСАННОЙ В ТРАПЕЦИЮ РАВЕН 18. НАЙДИТЕ ВЫСОТУ ЭТОЙ ТРАПЕЦИИСкачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
Радиус описанной окружности трапецииСкачать
ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать
ОГЭ Задание 24 Вписанная трапецияСкачать
Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать
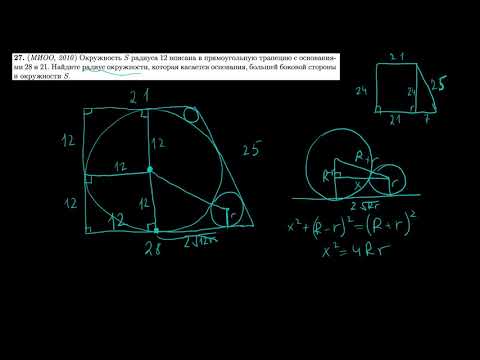
Математика ОГЭ Задание 24 Описанный вписанная окружность, трапецияСкачать
Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Планиметрия 3 | mathus.ru | трапеция и окружностьСкачать
Трапеция, решение задач. Вебинар | МатематикаСкачать
Вебинар №64. Математика. Планиметрия. №16 из ЕГЭ. Убийство трапеции. Дополнительные построенияСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
