Начертите остроугольный разносторонний треугольник и описать около него окружность

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Площадь треугольника
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

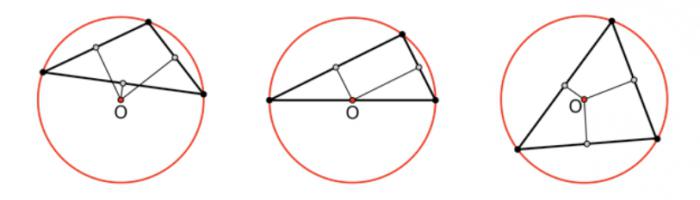
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

l = 2Rsin φ .

(1)

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Построй окружность, описанную около треугольника ABC, если треугольник ABC: а) остроугольный; б) прямоугольный; в) тупоугольный.

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Тупоугольный разносторонний треугольник и вписать в него окружность

Тупоугольный треугольник: длина сторон, сумма углов. Описанный тупоугольный треугольник

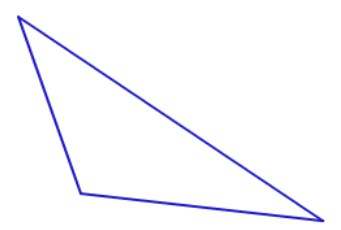
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является тупым углом.

Разбираемся с понятиями

В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.

Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения площади треугольника математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.

Правильное начертание

Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о .

Основные линии

Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.

Так, биссектрисы делят угол пополам, а противоположную сторону – на отрезки, которые пропорциональны прилегающим сторонам.

Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2 : 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.

Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.

Серединный перпендикуляр – это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.

Работа с окружностями

В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.

Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.

Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.

Вписанные треугольники

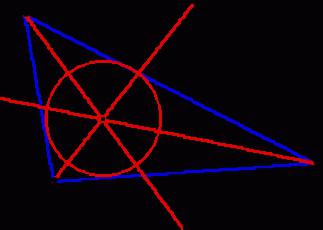
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном – за его пределами.

Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R – это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о .

Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.

Описанные треугольники

Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.

Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.

Радиус такой окружности, вписанной в тупоугольный треугольник, равняется квадратному корню из частного (p-c) х (p-v) х (p-b) : p. При этом p – это полупериметр треугольника, c, v, b – его стороны.

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

l = 2Rsin φ .

(1)

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

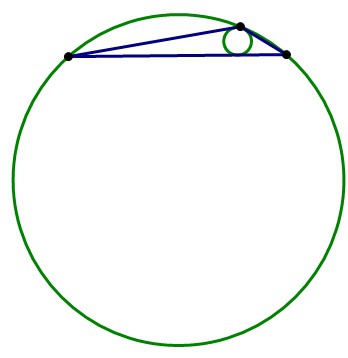
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .