Тупоугольный треугольник формула площади

Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Что такое тупоугольный треугольник

Тупоугольный треугольник — геометрическая фигура на плоскости, которая представляет собой треугольник, один из углов которого является тупым, то есть больше 90º.

Такой треугольник не может быть прямоугольным и равносторонним, но может быть равнобедренным.

Сумма углов треугольника равна 180º. Именно поэтому только один из них может быть больше 90º, два других всегда острые. Это единственная особенность данной фигуры. Подход к решению задач с такой фигурой не отличается от решения задач с треугольниками других типов.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Элементы тупоугольного треугольника

Помимо сторон и углов, тупоугольный треугольник имеет следующие элементы:

1. Внешний угол — тот, который смежен с внутренним, всего их шесть, по два на один внутренний. Внешний угол тупого всегда будет острым, острого — тупым.
2. Медиана — отрезок, который соединяет вершину треугольника с противолежащей стороной и делит ее пополам. Все медианы пересекаются друг с другом в одной точке (центроиде). Эта точка делит медианы в соотношении 2:1, считая от вершины.
3. Высота — перпендикуляр, который проведен из высоты треугольника на противоположную сторону. В тупоугольном треугольнике может лежать за пределами фигуры.
4. Биссектриса — прямая, делящая угол пополам. Делит противоположную сторону на отрезки, которые пропорциональны прилежащим сторонам фигуры. Точка, которая является пересечением биссектрис, также является центром вписанной окружности.

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Формулы площади тупоугольного треугольника

Для нахождения площади, периметра и других показателей тупоугольного треугольника используются те же формулы, что и для вычисления любого произвольного треугольника.

Площадь данной фигуры можно найти при помощи следующих формул:

S = ½ * x * h , где х — сторона;

S = √ p * ( p — x ) * ( p — y ) * ( p — z ) ,

p — полупериметр, p = ( x + y + z ) / 2

S = x * y * z / 4 * R , R — радиус описанной окружности;

S = p * r , p — полупериметр, r — радиус вписанной окружности.

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Пример решения задачи

Найти площадь тупоугольного треугольника, у которого стороны равны x=9, y=5, z=6.

Для решения задачи стоит использовать формулу площади с полупериметром.

p = ( x + y + z ) / 2 , p = ( 9 + 5 + 6 ) / 2 = 20 / 2 = 10 .

S = √ p * ( p — x ) * ( p — y ) * ( p — z ) , S = √ 10 * ( 10 — 9 ) * ( 10 — 5 ) * ( 10 — 6 ) = √ 10 * 1 * 5 * 4 = √ 200 = 10 √ 2

Видео:Тупоугольный треугольник для острого умаСкачать

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

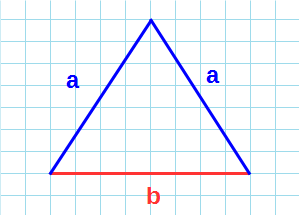
Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

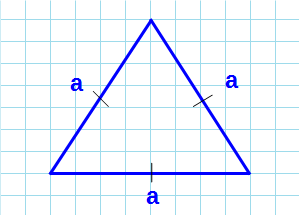
Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

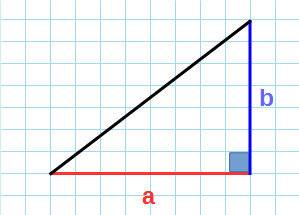
Если известна сторона и высота

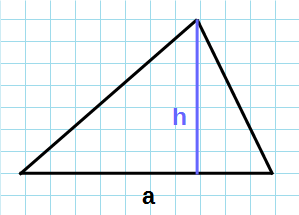
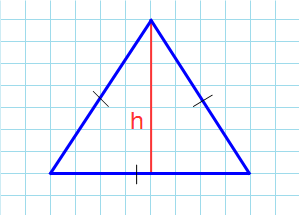
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

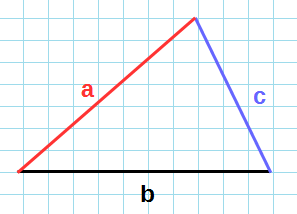
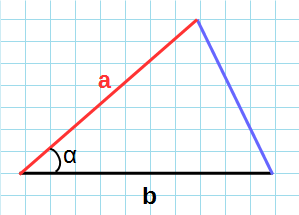
Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:11 класс, 47 урок, Формулы площади треугольникаСкачать

Если известны три стороны и радиус описанной окружности

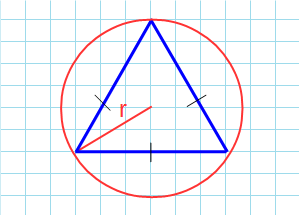
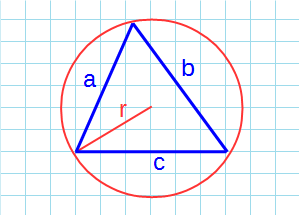
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:Найти площадь треугольника АВС. Задачи по рисункамСкачать

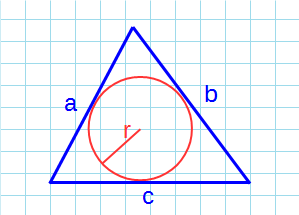
Если известны три стороны и радиус вписанной окружности

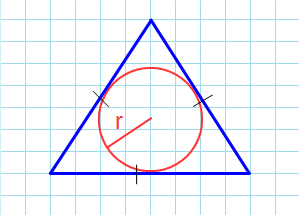
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

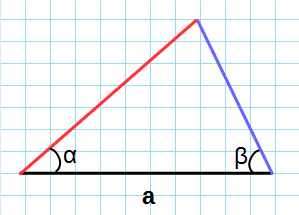
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

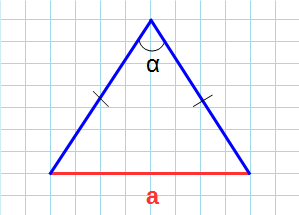
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

📸 Видео

Секретные формулы площади треугольникаСкачать

100. Теорема о площади треугольникаСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Виды треугольниковСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать