Какие из следующих утверждений верны?
1) Около любого ромба можно описать окружность.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
Проверим каждое из утверждений.
1) «Около любого ромба можно описать окружность.»— неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.
2) «В любой треугольник можно вписать не менее одной окружности.» — верно, в любой треугольник можно вписать окружность.
3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.
4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
- Описанная окружность
- Доказательство
- Доказательство
- Доказательство
- Доказательство
- Доказательство
- Ромб. Формулы, признаки и свойства ромба
- Признаки ромба
- Основные свойства ромба
- Сторона ромба
- Формулы определения длины стороны ромба:
- Диагонали ромба
- Формулы определения длины диагонали ромба:
- Периметр ромба
- Формула определения длины периметра ромба:
- Площадь ромба
- Формулы определения площади ромба:
- Окружность вписанная в ромб
- Формулы определения радиуса круга вписанного в ромб:
- 📹 Видео
Видео:Вписанная и описанная окружность - от bezbotvyСкачать
Описанная окружность
Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.
Теорема
| Около любого треугольника можно описать окружность. |
Доказательство
Дано: произвольный 
АВС.
Доказать: около АВС можно описать окружность.
Доказательство:
1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).
Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.
Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
| В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 . |
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).
Углы В и D — вписанные, тогда по теореме о вписанном угле: 
В = 
АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 
360 0 = 180 0 . Что и требовалось доказать.
Верно и обратное утверждение:
| Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность. |
Доказательство
Дано: четырехугольник АВСD, BАD + BСD = 180 0 .
Доказать: около АВСD можно описать окружность.
Доказательство:
Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).
ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)
Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСD
ВАD.
BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).
Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .
Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.
Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)
В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)
F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)
Подставим (3) и (4) в (2), получим:
С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, С
ВАD.
А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.
Примечание:
Окружность всегда можно описать:
Поделись с друзьями в социальных сетях:
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Ромб. Формулы, признаки и свойства ромба
 |  |
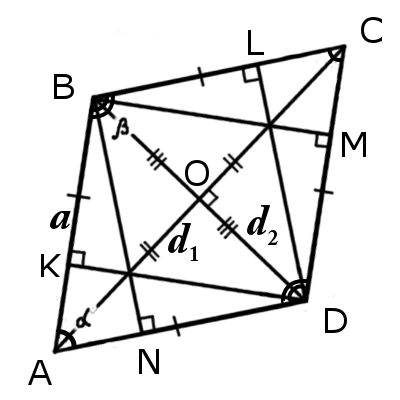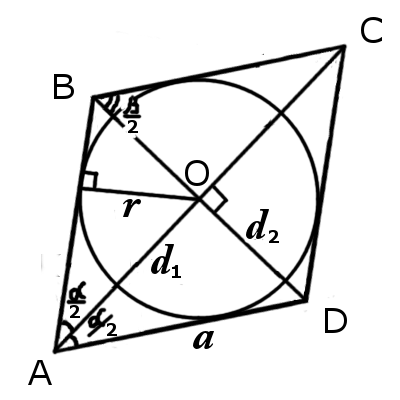| Рис.1 | Рис.2 |
Видео:Радиус вписанной в ромб окружности (6701)Скачать
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Видео:Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
4. Формула стороны ромба через две диагонали:
| a = | √ d 1 2 + d 2 2 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
| a = | d 1 |
| √ 2 + 2 cosα |
| a = | d 2 |
| √ 2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 — 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 — 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
| S = | 1 | d 1 d 2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4 r 2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
📹 Видео
Радиус описанной окружностиСкачать
Геометрия Докажите, что если около ромба можно описать окружность, то этот ромб является квадратомСкачать
Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать
№700. Докажите, что в любой ромб можно вписать окружность.Скачать
Площадь ромба. Легче понять...Скачать
ОГЭ ЗАДАНИЕ 16 ЦЕНТР ОКРУЖНОСТИ ОПИСАННОЙ ОКОЛО ТРЕУГОЛЬНИКА АБС ЛЕЖИТ НА СТОРОНЕ АБ РАДИУС 14,5Скачать
8. Ортоцентр и центр описанной окружности. РасстоянияСкачать
ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать
Вписанная и описанная около равнобедренного треугольника, окружностьСкачать
