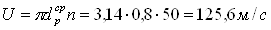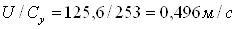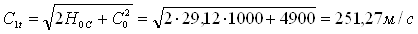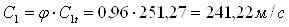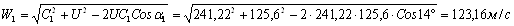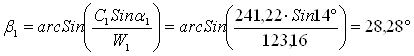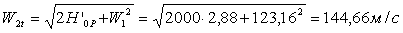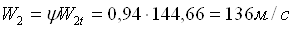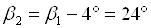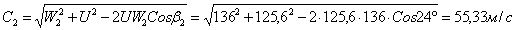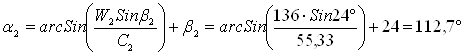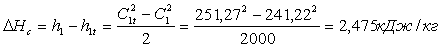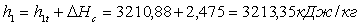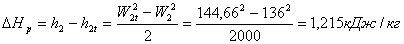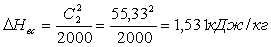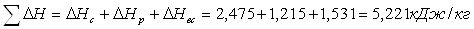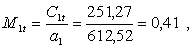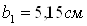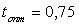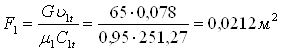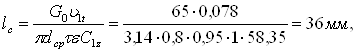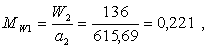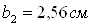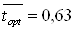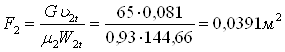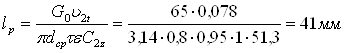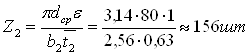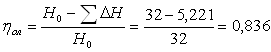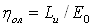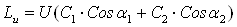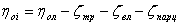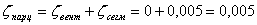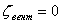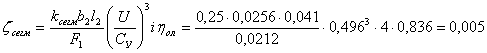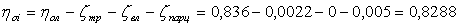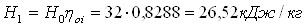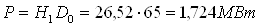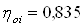Построение векторного треугольника скоростей (5 видео)

Использование радиолокатора для расхождения

Обработка радиолокационной информации включает определенную последовательность действий:

• наблюдение и обнаружение целей;
• глазомерную оценку опасности радиолокационной ситуации сближения и отбор целей для радиолокационной прокладки;
• радиолокационную прокладку — определение элементов движения цели и параметров ситуации сближения;
• расчет маневра расхождения;
• контроль за изменением радиолокационной ситуацией во время маневра до полного расхождения судов.

Наблюдение и обнаружение целей. Использование РЛС наиболее эффективно, если радиолокационное наблюдение ведется постоянно. В открытом море постоянное наблюдение следует вести на шкалах среднего масштаба 8—16 миль с периодическим осмотром обстановки на шкалах как более мелкого, так и более крупного масштабов. В стесненных водах постоянное наблюдение обычно ведется на шкалах крупного масштаба с периодическим обзором обстановки на мелкомасштабных шкалах.

Глазомерная оценка радиолокационной ситуации. Глазомерная оценка является обязательным этапом обработки радиолокационной информации и позволяет при большом количестве целей отобрать для прокладки опасные и потенциально опасные цели. Глазомерная оценка производится по следу послесвечения, который остается на экране РЛС за эхо-сигналом цели и представляет собой предыдущую траекторию относительного сближения судов. Мысленным продолжением следа послесвечения за эхо-сигналом цели получается линия относительного сближения (ЛОД), по которой определяют дистанцию кратчайшего сближения Дкр.

Глазомерную оценку опасности столкновения можно использовать только тогда, когда судоводитель понимает принцип построения треугольника скоростей, т.е. имеет достаточный навык работы на маневренном планшете.

При глазомерной оценке радиолокационной ситуации для выделения потенциально опасных целей, которые становятся опасными при маневре собственного судна и цели, чрезвычайно важно четко представлять направление разворота ЛОД, которое происходит в результате этих маневров.

Все возможные схемы перемещения эхо-сигналов охватывают следующие три начальные ситуации.

1. Эхо-сигнал перемещается параллельно курсовой черте нашего судна — это может быть встречное судно, обгоняемое судно, обгоняющее судно или неподвижная цель:
• при изменении скорости одного или обоих судов параллельность перемещения эхо-сигнала сохраняется;
• при изменении курса нашего судна ЛОД разворачивается в сторону, противоположную стороне разворота;
• разворот ЛОД (следа послесвечения), если наше судно не маневрировало, указывает на изменение курса цели в сторону разворота;
• эхо-сигнал неподвижной цели всегда перемещается параллельно линии курса нашего судна.

2. Эхо-сигнал перемещается не параллельно курсовой черте:
— через начало развертки — существует опасность столкновения;
— через курсовую линию нашего судна — цель пересекает нашкурс;
— по линии, проходящей по корме нашего судна, — наше судно пересечет или уже пересекло курс цели:
• при изменении направления или скорости перемещения эхосигнала, если наше судно не маневрировало, глазомерно нельзя сделать однозначного вывода о виде маневра цели. Вид маневра можно установить только с помощью радиолокационной прокладки;
• разворот нашего судна в сторону эхо-сигнала цели приводит к развороту ЛОД от кормы к носу нашего судна;
• уменьшение скорости нашего судна приводит к развороту ЛОД от кормы к носу нашего судна;
• увеличение скорости нашего судна приводит к развороту ЛОД от носа к корме нашего судна;
• отворот нашего судна от эхо-сигнала не позволяет глазомерно оценить эффективность этого маневра (уменьшается относительная скорость сближения, увеличивается tкр и в результате может произойти резкое изменение направления ЛОД, определяемое только при радиолокационной прокладке).

3. Эхо-сигнал не перемещается — судно-сателлит:
• появление следа послесвечения параллельно курсовой черте —изменение скорости одного или обоих судов;
• изменение курсов одного или обоих судов вызывает появление следа послесвечения, не параллельного курсовой черте.

Радиолокационная прокладка. Относительная прокладка — выполняется на маневренном планшете путем построения векторного треугольника скоростей. С использованием относительной прокладки легко можно определить элементы движения цели и параметры ситуации сближения. Поэтому она является основным методом, используемым на практике.

Главное, что интересует судоводителя при обнаружении объекта на экране радиолокатора – насколько опасна наблюдаемая цель.

Степень опасности оценивается по двум критериям:
1. Дкр – дистанция кратчайшего сближения – минимальное расстояние, на которое цель может приблизиться к нашему судну, если
никто не будет изменять элементы своего движения (курс и скорость);
2. tкр – интервал времени до точки кратчайшего сближения – интервал времени от момента получения последней точки цели, на основании которой строится линия относительного движения ЛОД, до момента приближения цели на кратчайшее расстояние к нашему судну.

Чем меньше Дкр, тем более опасной является приближающаяся цель. Но нельзя оценивать степень опасности только по дистанции
кратчайшего сближения. Не менее важными факторами являются скорость сближения и запас времени, которым располагает судоводитель, чтобы предпринять маневр и разойтись на безопасном расстоянии. Так ситуация обгона, как правило, менее опасна чем расхождение на встречных (пересекающихся) курсах, даже если Дкр в первом случае меньше, чем во втором.

Построение треугольника скоростей

Суть относительной прокладки заключается в том, что за центр системы координат мы принимаем наше судно, которое помещаем в центр планшета, а цели наносим на планшет в соответствующие точки по пеленгу и дистанции, измеренных при помощи РЛС.

Пошаговые действия для оценки ситуации:

1. в центр планшета наносится вектор скорости нашего судна, равный 6-ти минутному отрезку (например, скорость нашего судна 15 узлов, откладываем по курсу 1, 5 мили);
2. делаются замеры пеленга и дистанции встречного судна;
3. в таблицу записываются данные измерения и на планшет наносится первая точка – А1;
4. в полученную точку параллельно переносится и “втыкается” вектор скорости нашего судна;
5. через 3 минуты повторяются пункты 2-3, наносится вторая точка А2. Приближенно оценивается ситуация сближения;
6. еще через 3 минуты повторяются пункты 2-3, наносится третья точка А3;
7. соединив точки А1 – А2 – А3, получаем линию относительного движения – ЛОД;
8. из начала нашего вектора скорости строим вектор Vв, который является вектором истинной скорости и курса встречного судна;
9. перпендикуляр, проведенный из центра планшета к ЛОД определяет Дкр (в нашем случае Дкр = 1,7 мили). Величину tкр находим, откладывая по ЛОД отрезки, равные V0 до Дкр (здесь, примерно, укладывается 1,5 V0, т.е. tкр = 1,5 х 6 мин = 9 мин);
10.принимается решение по выбору маневра расхождения.

Построение треугольника скоростей

Содержание

Маневр расхождения курсом
Маневр расхождения скоростью
ЗАКОНОМЕРНОСТИ СБЛИЖЕНИЯ СУДОВ
Построение треугольников скоростей
📺 Видео

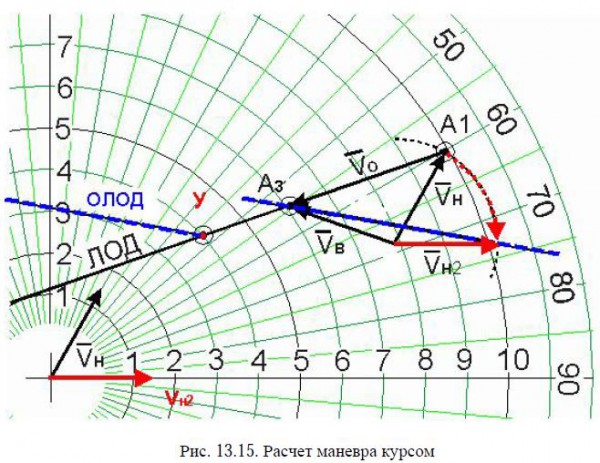
Маневр расхождения курсом

1. Необходимо на ЛОД нанести упреждающую точку У положения цели в момент начала нашего маневра. Обычно это 3-х минутный интервал (расстояние А1 – А2).
2. Из этой точки У проводим касательную к окружности, величина которой соответствует заданной дистанции расхождения (здесь 3 мили).
3. Полученную прямую ожидаемой линии относительного движения ОЛОД переносим параллельно самой себе в точку А3.
4. Вектор нашего судна Vн при помощи циркуля разворачиваем до тех пор, пока он не пересечется с ОЛОД.
5. Полученный вектор Vн2 переносим в центр планшета и определяем новый курс нашего судна, который необходим для расхождения с целью на расстоянии в 3 мили.

Расчет маневра курсом

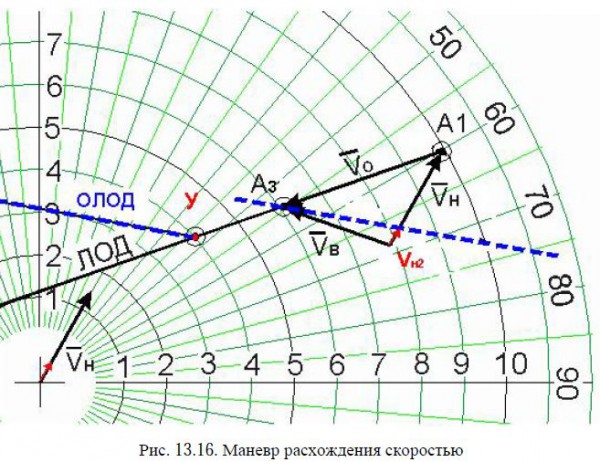
Маневр расхождения скоростью

1. Необходимо на ЛОД нанести упреждающую точку У – положение цели в момент начала нашего маневра. Обычно это 3-х минутный интервал (расстояние А1 – А2).
2. Из точки У проводим касательную к окружности, величина которой соответствует заданной дистанции расхождения (здесь 3 мили).
3. Полученную прямую ожидаемой линии относительного движения ОЛОД переносим параллельно самой себе в точку А3.
4. ОЛОД «отсекает» часть вектора нашего судна. Отрезок от начала вектора до точки пересечения с ОЛОД откладываем на векторе в
центре планшета. Это и есть новая скорость нашего судна, необходимая для расхождения на заданной дистанции.
5. Снижение скорости необходимо начинать заранее – до наступления момента У, с тем, чтобы в этот момент судно уже имело новую скорость.

Маневр расхождения скоростью

Маневр расхождения скоростью применим для судов водоизмещением до 20000 тонн. В любом случае, при выполнении маневра расхождения необходимо учитывать маневренные характеристики судна.

При выборе маневра расхождения с опасной целью, когда на экране наблюдаются эхо-сигналы других судов, необходимо учитывать те из них, ситуация сближения с которыми может ухудшиться в результате выбранного маневра. Такие опасные суда определяются глазомерно по направлению разворота ЛОД при предполагаемом маневре. Особенность радиолокационной прокладки в этом случае заключается в необходимости одновременного ее ведения для всех потенциально опасных судов. Как правило, на планшет наносится полный анализ ситуации до момента окончания маневра и возвращения к исходным параметрам движения вашего судна.

Видео:Сложение векторов. 9 класс.Скачать

ЗАКОНОМЕРНОСТИ СБЛИЖЕНИЯ СУДОВ

Треугольник скоростей, ведение относительной прокладки на маневренном планшете

Обработка радиолокационной информации при использовании любых технических средств, сводится к решению векторного треугольника скоростей.

Основным элементом векторного треугольника скоростей является вектор относительной скорости перемещения эхо-сигнала цели Vo, направление и величина которого обусловлены векторами скоростей нашего судна Vn и судна-цели Vu, т.е. Vo = Vn — Vu .

В свою очередь, вектор относительной скорости определяет направление ЛОД и величину относительной скорости v.

В геометрическом плане безопасность расхождения с целью достигается таким разворотом ЛОД за счет изменения вектора относительной скорости, в результате которого D кр станет не менее заданной величины, т.е. D кр >= D зад.

Поскольку вектор скорости цели от нас не зависит, изменение вектора относительной скорости может быть достигнуто только изменением вектора нашего судна, т.е. маневром курсом и/или скоростью.

НАЧАЛЬНЫЕ ПОСТРОЕНИЯ И ОЦЕНКА СИТУАЦИИ

Главное, что интересует судоводителя при обнаружении объекта на экране радиолокатора — насколько опасна наблюдаемая цель. Степень опасности оценивается по двум критериям:

1. Дк_Р — Дистанция кратчайшего сближения — минимальное расстояние, на которое цель может приблизиться к нашему судну, если никто не будет изменять элементы своего движения (курс и скорость);
2. t_Kp — Интервал времени до точки кратчайшего сближения —интервал времени от момента получения последней точки цели, на основании которой строится линия относительного движения ЛОД, до момента приближения цели на кратчайшее расстояние к нашему судну.

Чем меньше Д_кр, тем более опасной является приближающаяся цель. Но нельзя оценивать степень опасности только по дистанции кратчайшего сближения. Не менее важными факторами являются скорость сближения и запас времени, которым располагает судоводитель, чтобы предпринять маневр и разойтись на безопасном расстоянии. Так ситуация обгона, как правило, менее опасна чем расхождение на встречных (пересекающихся) курсах, даже если Д_Кр в первом случае меньше, чем во втором.

Использование маневренного планшета при расхождении судов сводится к ведению так называемой «относительной прокладки». Суть относительной прокладки заключается в том, что за центр системы координат мы принимаем наше судно, которое помещаем в центр планшета, а данные пеленгов и дистанций интересующих нас объектов наносим на планшет в соответствующие точки пересечения окружностей дальности и лучей пеленгов (рис. 13.).

Для оценки опасности наблюдаемого объекта необходимо построить линию относительного движения ЛОД (линию, по которой относительно нас будет двигаться встречное судно). Для построения ЛОД необходимо, как минимум, две последовательные во времени точки на планшете (рис. 14).

Проведя линию от точки А1 к точке А2 мы получим направление относительного движения встречного судна (вектор относительной скорости Vo). А если линию, проходящую через точки А1 и А2, продлить, то получим линию относительного движения. Вектор относительной скорости есть результат разницы векторов:

Резонно предположить, что если ни одно из судов нс изменит элементов своего движения (курса и скорости), то через такой же интервал времени встречное судно продвинется в том же направлении на такое же расстояние (рис. 15.).

Резонно предположить, что если ни одно из судов не изменит элементов своего движения (курса и скорости), то через такой же интервал времени встречное судно продвинется в том же направлении на такое же расстояние (рис. 16).

Из рисунка видно, что вектор относительной скорости V₀2 не отличается от Voi только в том случае, когда векторы скоростей обоих судов не меняются.

При ведении прокладки на планшете мы не знаем изначально, маневрирует ли встречное судно, но имеем векторы относительной скорости V₀2 и Voi. То есть, решаем обратную задачу: если вектор относительной скорости V₀2 не отличается от V_oi, и вектор скорости нашего судна V_H не менялся, то следовательно, вектор скорости встречного судна V_B гак же не менялся.

На планшете это выражается в том, что три последовательные точки Al, А2 и АЗ лежат на одной прямой, и расстояние [А1;А2] равно расстоянию [А2;АЗ].

ЛОД, построенная на двух последовательных точках, не гарантирует, что встречное судно не маневрирует.

Можно быть уверенным, что встречное судно не маневрирует, только в том случае, если его три последовательных точки, взятые через равные промежутки времени, лежат на планшете на одной прямой, и расстояние между ними одинаковое.

Встречное судно A меняет курс.

Встречное судно А меняет скорость.

Частный случай, когда в результате изменения встречным судном А своего курса и скорости ЛОД нс изменяется

Из рисунков видно, что если встречное судно изменило курс и/или скорость, то вектор относительной скорости V₀2 отличается от V_oi как минимум по величине (рис. 17.в), а как правило, и по величине, и по направлению.

Следует отметить, что на практике измерения пеленга и дистанции производятся с некоторой погрешностью, зависящей как от технических характеристик РЛС, так и от самого судоводителя. Поэтому, последовательные точки А1-АЗ могут и не лежать на одной прямой, даже если элементы движения обоих судов не меняются (рис. 18).

Следует помнить, что судоводители стремятся избегать несущественных изменений элементов движения судна (МППСС-72, Правило 8 Ь).

Следовательно, то, что через равные интервалы времени точки ложатся с небольшим отклонением по направлению и расстоянию между ними, как правило, связано именно с погрешностью определения пеленга и дистанции цели.

В этом случае ЛОД должна быть проведена на равноудаленном, по возможности, от точек расстоянии, нс превышающем срсднсквадратичсской погрешности Мо определения места судна данным способом.

Если через три точки (с учетом среднеквадратической погрешности их определения М_о) невозможно провести прямую, то это значит, что встречное судно в данное время изменяло свои элементы движения.

Краткий вывод по теме.

Пошаговые действия для оценки ситуации:

— наносится вектор скорости нашего судна
— делаются замеры пеленга и дистанции встречного судна
— в таблицу записываются соответствующие данные
— на планшете ставится точка, соответствующая положению встречного судна
— в полученную точку параллельно переносится и «втыкается» вектор скорости нашего судна
— через 6 мин. повторяются пункты 2-4
— еще через 6 мин. повторяются пункты 2-4
— по трем точкам строится ЛОД
— достраиваются векторы У_ои V_B
— оценивается ситуация и принимается решение

РАСЧЕТ МАНЕВРА РАСХОЖДЕНИЯ

Расчет маневра расхождения заключается в том, чтобы направить линию относительного движения на безопасное расстояние от нашего судна. Поскольку маневр невозможно предпринять мгновенно в момент получения последней точки наблюдения (на основе которой производится оценка ситуации), необходимо принять точку упреждения У — точку, в которой будет встречное судно в момент, когда вы предпримите маневр (рис. I).

Примечание. В принципе, точка У выбирается произвольно, однако, на практике удобнее се устанавливать через интервал времени, кратный интервалу времени между наблюдениями, т.к. в этом случае достаточно измерителем снять расстояние между точками наблюдения и отложить этот раствор от последней точки на продолжение ЛОД. Поскольку время между наблюдениями обычно принимается 6 мин., то и точка упреждения устанавливается через интервал, кратный 6 мин.

Мы знаем, что направление ЛОД (ОЛОД) определяется направлением вектора относительной скорости. А вектор относительной скорости мы можем изменить лишь изменив вектор собственной скорости (рис.20).

Предположим, что мы решили разойтись на дистанции 3 мили. Это значит, что Л ОД должна пройти по касательной к окружности, соответствующей 3-мильной дистанции. Проведя из точки У касательную к 3-мильной дистанции мы получим ОЛОД — ожидаемую линию относительного движения.

Но для получения необходимой ОЛОД нужно так изменить векторный треугольник, чтобы новый вектор V_o лежал на ОЛОД. Этого можно было бы добиться, построив новый векторный треугольник при точке У (рис.21)

1. переносим в т.У вектор скорости встречного судна V„ без изменения (поскольку оно нс маневрирует)
2. продляем ОЛОД вправо от т. У для построения вектора V₀2 из начала вектора V_B (точка 02) откладывает вектор нашей скорости V_H в таком направлении, чтобы сто конец ложился на ОЛОД

Полученное таким образом новое направление вектора скорости нашего судна и есть искомый курс расхождения на заданной дистанции.

Важно обратить внимание на соответствие длины вектора V_H , «воткнутого» в т.А1, интервалу времени между первой и последней точками встречного судна. Если этот интервал времени составляет 6 мин., то и длина вектора Vu должна соответствовать расстоянию, проходимому за 6 мин. Если этот интервал времени составляет, например, 9 или 12 мин., то и длина вектора V_H должна соответствовать расстоянию, проходимому за 9 или 12 мин. соотве гстве!11ю. Все векторы «скоростного треугольника» соответствуют одному и тому же временному интервалу.

Рассмотренное на рис.З построение загромождает планшет и требует выполнения построений, которых можно избежать. Более экономичным по времени решением является следующее (рис.22):

1.0Л0Д параллельно переносится в т.А2
2.вектор Ун поворачивается относительно т.0 таким образом, чтобы лечь острием на линию, параллельную ОЛОД

! Вектор Vh 2 — это вектор, показывающий курс и скорость, которые должно иметь наше судно после маневра чтобы разойтись со встречным судном на дистанции 3 мили, если маневр будет совершен в данной точке упреждения т.У.

Следует обратить внимание на то, что рассмотренный пример предусматривает маневр только путем изменения курса нашего судна. Если бы задача решалась только с точки зрения геометрии, то мы бы имели целый сектор возможных сочетаний курсов и скоростей, которые бы удовлетворяли поставленной задаче (ри.23).

Из рисунка видно, что любой вектор Vh, опирающийся острием на снесенную ОЛОД, задает нужное направление вектора относительной скорости (меняется только величина V02):

• изменение вектора Vh только по направлению соответствует маневру изменением только курса;
• изменение вектора V_H только по величине соответствует маневру изменением только скорости;
• изменение вектора Vh по величине и направлению соответствует маневру изменением курса и скорости.

На рис.5 рассмотрен только сектор возможных сочетаний курсов и скоростей, которые направят встречное судно точно по ОЛОД. Но обычно ставится задача не точного расхождения на заданной дистанции, а расхождение на дистанции не ближе заданной. Посмотрим, как будет проходить ОЛОД при различных курсах нашего судна (рис.24).

Примечание. Красным цветом обозначены варианты, когда ОЛОД проходит ближе заданной дистанции 3 мили.

! На основании вышеизложенного можно утверждать, что любое сочетание курса и скорости нашего судна обеспечит расхождение на дистанции, нс ближе заданной, если вектор V_H будет находиться в пределах заштрихованного сектора (рис.25).

Это был рассмотрен вариант, когда мы планируем расходиться со встречным судном левым бортом. Если делать сразу предварительную оценку возможности расхождения и правым бортом, то на планшете необходимо провести точно такие же построения и справа од нашего судна:

• провести ОЛОД справа;
• снести ОЛОД в точку А2;
• определить сектор возможных сочетаний курса и скорости.

Из множества возможных вариантов судоводитель должен выбрать оптимальный, руководствуясь рядом условий:

• соблюдение правил МППСС;
• наличие других судов;
• наличие навигационных опасностей;
• особенности своего судна;
• другие обстоятельства, могущие повлиять на безопасность маневра.

В общем случае маневр курсом предпочтительнее маневра скоростью. Дело в том, что на изменение скорости требуется больше времени, чем на изменение курса, и кроме того, потеря скорости превращает судно в пассивного наблюдателя за развитием ситуации. И если ситуация начнет развиваться в опасную сторону, то потерявшее скорость судно будет уже не в состоянии предотвратить столкновения поскольку на разгон судна уходит существенно больше времени, чем на торможение. Только для относительно небольших судов нет разницы как маневрировать при расхождении — курсом или скоростью.

И еще одно замечание. Обычно, при расчете маневра курсом просто поворачивают вектор своей скорости, как было рассмотрено в примере (рис.4). Правила МППСС требуют при расхождении избегать небольших изменений курса, чтобы другое судно могло однозначно понимать ваш маневр. Исходя из этого обычно рекомендуется в подобных случаях изменять курс не менее чем на 30°. Однако, выход судна на циркуляцию всегда приводит к падению скорости (так при повороте на контркурс падение скорости может достигать 50% от первоначальной скорости). Это не всегда может иметь существенное значение, но помнить об этом следует.

Краткий вывод по теме.

Пошаговые действия для расхождения с одним судном:

1 .наносится вектор скорости нашего судна
2. делаются замеры пеленга и дистанции встречного судна
3. в таблицу записываются соответствующие данные
4. на планшете ставится точка, соответствующая положению встречного судна
5. в полученную точку параллельно переносится и «втыкается» вектор скорости нашего судна
6.через 3 мин. повторяются пункты 2-4
7. еще через 3 мин. повторяются пункты 2-4
8. по трем точкам строится ПОД
9. достраиваются векторы У_ои V»
10. оценивается ситуация и принимается решение предпринять маневр
11. устанавливается точка упреждения
12. прокладывается ОЛОД
13. ОЛОД параллельно сносится в последнюю точку «скоростного треугольника» (треугольника, образованного векторами V_H. V_Bn V_o)

14. вектор V_H поворачивается (и/или изменяется его длина) таким образом, чтобы его острие легло на снесенную ОЛОД
15. снимается новое направление и величина вектора скорости нашего судна: новое направление соответствует новому курсу нашего судна, а величина — скорости для заданного расхождения.

РАСХОЖДЕНИЕ С НЕСКОЛЬКИМИ СУДАМИ

Расчет маневра для расхождения с несколькими судами до определенного этапа ведется точно так же, как и при расхождении с одним судном:

1 . наносится вектор скорости нашего судна
2. в таблицу записываются данные пеленгов и дистанций встречных судов, полученные на РЛС
3. на планшете ставятся точки, соответствующие положению встречных судов
4. в полученные точки параллельно переносится и «втыкается» вектор скорости нашего судна
5. через 6 мин, повторяются пункты 2, 3
6. еще через 6 мин, повторяются пункты 2, 3
7. по трем последовательным точкам строятся ЛОДы для всех судов
8. достраиваются векторы У_ои У_вдля всех судов
9.оценивается ситуация и принимается решение предпринять маневр
10. устанавливаются точки упреждения на ЛОДах (все они должны соответствовать одному и тому же судовому времени)
11. прокладываются ОЛОДы к заданной дистанции расхождения (в примере Д_кр=2мили)
12. ОЛОДы параллельно сносятся в последние точки соответствующих «скоростных треугольников»
13. в каждом скоростном треугольнике вектор Ун поворачивается (и/или изменяется ею длина) таким образом, чтобы его острие легло па снесенную ОЛОД
14. снимаются новые направления и величины вектора скорости нашего судна из которых выбирается то, которое обеспечит расхождение со всеми судами па безопасном расстоянии. Как правило, это соответствует варианту с наибольшим отклонением от первоначального курса.
15. выбранный новый вектор Ун сносится параллельно во все скоростные треугольники
16. достраиваются новые векторы Уо
17. определяются новые ОЛОДы, задаваемые соответствующими векторами Уо
18. в судовое время, соответствующее точке упреждения, совершается маневр и делаются контрольные определения местоположения судов с занесением в таблицу соответственных данных

Внимание! Часто встречающейся ошибкой является попытка решить задачу расхождения, производя построения только при встречном судне, являющимся наиболее опасным до начала маневрирования. Ситуация часто складывается таким образом, что судно, которое могло бы пройти на безопасном расстоянии, становится опасным из-за того, что наше судно начало маневрировать. Поэтому, во-первых, следует производить предварительный расчет при всех цслях/судах, а во-вторых, совершенно необходимо выполнить пункты 16-18, чтобы убедиться, что выбранный вами маневр обеспечивает безопасное расхождение со всеми судами.

ИСПОЛЬЗОВАНИЕ ЛОГАРИФМИЧЕСКОЙ ШКАЛЫ

1. Известны точки последовательных относительных местоположений встречного судна и соответствующий интервал времени между ними: необходимо найти относительную скорость.
2. Известна относительная скорость встречного судна: необходимо

определить точку, в которой оно окажется в заданное время.

3. Известна относительная скорость встречного судна: необходимо

определить время, через которое оно окажется в заданной точке.

1 Любая задача по определению элементов относительного движения начинается с измерения величины вектора относительной скорости, т.с. измеряется расстояние, пройденное встречным судном (целью) относительно нашего судна (рис.26):

о измерителем снимается расстояние между последовательными точками;

о полученный раствор измерителя переносится на оцифрованную шкалу, где и определяем расстояние между точками.

Примечание. Настоятельно рекомендуем не втыкать иголку измерителя в центр планшета, т.к. это слишком быстро приводит к образованию дырки в центре, что делает планшет неудобным в работе!

2. Теперь нам известно пройденное расстояние и время. Переходим к логарифмической шкале. За 6 минут пройдено 3,9 мили, поэтому одну ножку измерителя устанавливаем на цифру 6, а другую — на цифру 3,9.

Примечание. Важно сохранить полученный раствор измерителя, поскольку любые дальнейшие измерения производятся именно этим раствором. Этот раствор связывает проходимое расстояние за определенное время.

относительного движения, то переносим измеритель (сохраняя раствор) в отметку 60, а другая ножка нам покажет соответствующее этому времени расстояние 39 миль. Поскольку скорость -это количество миль за 60 минут, полученная величина и будет соответствовать относительной скорости 39 узлов.

будет встречное судно через 15 минут, то переносим измеритель (сохраняя

раствор) одной ножкой в отметку 15, а другая ножка нам покажет

соответствующее этому времени расстояние 9,7 мили. Делаем раствор циркуля 9,7 мили по шкале планшета и откладываем это расстояние от последней точки по ЛОД -получаем будущее

местоположение встречного судна через 15 минут.

Если до контрольной точки встречному судну осталось пройти 8 миль, то для нахождения времени

(сохраняя раствор) одной ножкой в отметку 8, а другая ножка нам покажет соответствующее этому расстоянию время 12,3 мин.

Использовать логарифмическую шкалу можно не только при определении элементов относительного движения, но и для решения тех же задач по истинному движению как своего судна, так и встречного. Только в этом случае в качестве первого шага измеряется вектор скорости своего судна или встречного соответственно.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Построение треугольников скоростей

2. Построение треугольников скоростей

Принимаем средный диаметр регулирующей ступени равному d_ср=0,8м

Тогда окружная скорость на среднем диаметру составляет

Отношение скорости U/C_у равняется

где 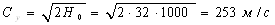— условная скорость, рассчитанная по изоэтропийному перепаду энтальпий на ступень.

Рассчитанное отношение скорости входит в диапазон , в котором находится максимальное значение η_oi для одновенечной ступени.

Теоретическая скорость истечения пара в сопловой решетке

Действительная скорость истечения пара в сопловой решетке

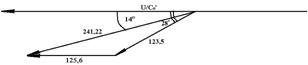
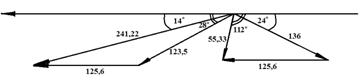
Построим треугольник скоростей для сопловой решетки. Принимаем угол выхода потока из сопловой решетки α₁=14°.

Рис.2. Треугольник скоростей сопловой решетки.

По треугольнику скоростей определили относительную скорость сопловой решетки W₁=123,5м/с и угол входа потока в рабочую решетку β=28°С.

Проверим эти значения расчетным путем. Относительная скорость пара на входе в рабочую решетку равна

Угол входа потока в рабочую решетку

Теоретическая относительная скорость пара на выходе из рабочей решетки

Действительная относительная скорость потока на выходе из рабочей решетки

Угол выхода потока пара из рабочей решетки

Действительная скорость на выходе из рабочей решетки

Угол входа потока в сопловую решетку второй ступени

Достроим треугольник скоростей

Рис.3 Треугольники скоростей сопловой и рабочей решеток

3. Расчет потери теплоперепада

Потеря теплоперепада в сопловой решетке составляет

Энтальпия пара после действительного расширения в сопловой решетке

Потеря теплоперепада в рабочей решетке составляет

Потеря с выходной скоростью в камере регулирующей ступени

Суммарная потеря составляет

4. Выбор тип профиля сопловой и рабочей решетки

Выбор профиля сопловой решетки

Теоретический удельный объем после расширения в сопловой решетке 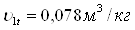по давлению р₁=3,7МПа и энтальпии h₁_t=3210,88кДж/кг.

Для подбора сопловой решетки исходными параметрами являются углы входа, выхода потока пара (α₁ и α₂) и также число Маха M_C₁. Число Маха составляет

где 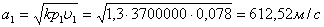— скорость звука в среде; k – показатель изоэнтропы (для перегретого пара k=1,3-1,34).

Выбираем профиль по /1/ С-90-15А

Хорда профиля

Шаг решетки

Площадь выходного сечения сопловой решетки

где 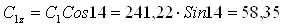— проекция на оси Z

Число сопловых лопаток

Выбор профиля рабочей решетки

Теоретический удельный объем отработавщего пара в рабочей решетке:

по давлению P₂=3,6МПа и энтальпии h₂_t=3208кДж/кг.

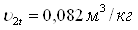
Для подбора рабочей решетки исходными параметрами являются углы входа, выхода потока пара (β₁ и β₂) и также число Маха M_W₁. Число Маха составляет

где 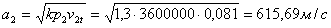— скорость звука в среде;

Выбираем профиль по /1/ Р-35-21А

Хорда профиля

Шаг решетки

Площадь выходного сечения рабочей решетки

Высота рабочих лопаток

где 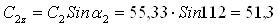— проекция на оси Z

Число рабочих лопаток

5. Расчет относительный лопаточный КПД

Относительный лопаточный КПД по потерям энергии

Для проверки правильности расчета η_ол определим относительный лопаточный КПД по треугольникам скоростей

— работа 1кг пара с учетом потерь в сопловом аппарате, на рабочей лопатке и с выходной скоростью, кДж/кг; кДж/кг – распологаемая энергия ступени при промежуточной ступени равно распологаемому теплоперепаду.

Относительный лопаточный КПД η_ол равняется

Погрешность относительного лопаточного КПД составляет

Для определения эффективности турбинной ступени определим внутренний относительный КПД :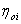

Потери от влажности составляет .

Потери от трения составляет

где 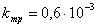— коэффициент трения; F₁=0,022м 2 – площадь выходного сечения сопловой решетки

Вентиляционные потери:

где 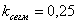— коэффициент сегмента; i=4 — число групп сопел

Внутренный относительный КПД равняется

Действительный теплоперепад ступени

Мощность регулируещей ступени

В данной курсовой работе был произведены расчет промежуточной (регулирующей) ступени турбоустановки. Определили углы входа и выхода турбинных решетек по треугольником скоростей. По полученными значениями углы выбирали профиль С-90-15А.

Были получены следующие результаты:

Относительный лопаточный КПД турбины

Внутренный относительный КПД турбины

Действительный теплоперепад ступени

Мощность регулирующей ступени

1. Тепловой расчет паровой турбины: учебное пособие для студентов теплоэнергетических специальностей / Под редакцией А.Н. Кудрящов, А.Г. Фролов. –Иркутск, – 2004. – 87с.

2. Паровые и газовые турбины / Под ред. А. Г. Костюка и В.В. Фролова, 4-е изд., стереотипное. М.: Энергоавтомиздат, 1985. – 351с.

3. Трухный А. Д. Стационарные паровые турбины: учебник для студентов технических вузов. Изд. 2-е, перераб. М.: Энергия, 1981. – 456 с.

4. Лекции по курсу «Тепловые двигатели», 2010г.

5. Диаграмма h,s для водяного пара.

6. Александров А. А., Григорьев Б. А. Таблицы теплофизических свойств воды и водяного пара: Справочник. Рек. Гос. службой стандартных справочных данных. ГСССД Р-776-98. – 2-е изд., стереот. – М.: Издательский дом МЭИ, 2006. – 168 с.