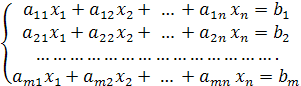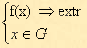Видео:Как разложить вектор по базису - bezbotvyСкачать
Проверить образуют ли вектора базис онлайн калькулятор
Базисом в -мерном пространстве называется упорядоченная система из линейно-независимых векторов.
Введём также некоторые дополнительные понятия, необходимые для дальнейшего изложения.
, где − некоторые числа и называется линейной комбинацией векторов .
Если существуют такие числа из которых хотя бы одно не равно нулю (например ) и при этом выполняется равенство:
, то система векторов − является линейно-зависимой.
Если же указанное равенство выполняется лишь при условии, что все числа , тогда система векторов − является линейно-независимой.
Базис может образовывать только линейно-независимая система векторов. Понятие линейной зависимости/независимости системы векторов, тесно связано с понятием ранга матрицы .
Наш онлайн калькулятор позволяет проверить образует ли система векторов базис. При этом калькулятор выдаёт подробное решение на русском языке.
Видео:Решение "базисной системы векторов" (2)Скачать
Алгоритм нахождения базиса системы векторов
Для того чтобы найти базис системы векторов Av А2. А , необходимо:
1) составить соответствующую системе векторов однородную систему уравнений
2) привести эту систему к равносильной разрешенной системе вида
- 3) записать базис системы векторов Б = (АрА2, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
- 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора
в разрешенной системе уравнений, т.е.
Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г. 
Пример 3.3. Найти ранг и базис системы векторов
разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.
Решение. Составим систему уравнений A t ay + А2х2 + . + А„хп = 0, которая в координатной записи имеет вид
Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.
Разрешенная система имеет вид
В базис системы векторов включаем 1-й и 2-й векторы Б: = (AVA2), которые соответствуют разрешенным неизвестным х1 и х2. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.
Запишем разложения векторов по базису. Коэффициентами разложения вектора А3 являются координаты вектора А’3 = (3, -2), т.е. коэффициенты при х3 в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х3 А3 = ЗЛ1 — 2Аг Аналогично, коэффициентами разложения вектора А4 являются координаты вектора А’4 = (4, 1) А4 = 4Ау + 1 Ат
Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я94 = 1.
Видео:Образуют ли данные векторы базисСкачать
Как найти базис данной системы векторов
Определение базиса.Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример 1.Базис пространства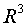 
: 
.
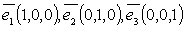
2. В системе векторов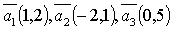 
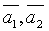
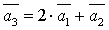
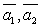
базисом являются векторы: 
, т.к. 
линейно выражается через векторы 
.
Замечание.Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
Теорема Кронекера-Капелли
Теорема Кронеккера–Капелли дает исчерпывающий ответ на вопрос о совместности произвольной системы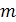 
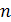
линейных уравнений с 
неизвестными
Теорема Кронеккера–Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы,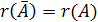 
.
Алгоритм отыскания всех решений совместной системы линейных уравнений вытекает из теоремы Кронеккера–Капелли и следующих теорем.
Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Алгоритм решения произвольной системы линейных уравнений:
1. Найдем ранги основной и расширенной матриц системы. Если они не равны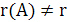 
( 
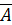
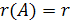
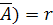
), то система несовместна (не имеет решений). Если ранги равны 
( 
, то система совместна.
2. Для совместной системы найдем какой-нибудь минор, порядок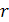 
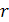
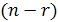
которого определяет ранг матрицы (такой минор называют базисным). Составим новую систему из уравнений, в которых коэффициенты при неизвестных, входят в базисный минор (эти неизвестные называют главными неизвестными), остальные уравнения отбросим. Главные неизвестные с коэффициентами оставим слева, а остальные 
неизвестных (их называют свободными неизвестными) перенесем в правую часть уравнений.
3. Найдем выражения главных неизвестных через свободные. Получаем общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образомнаходим частные решения исходной системы уравнений.
Линейное программирование. Основные понятия
Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.
Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.
Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующихсистему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называетсядопустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.
Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).
В общей постановке задача линейного программирования выглядит следующим образом:
Имеются какие-то переменные х = (х1 , х2 , … хn ) и функция этих переменных f(x) = f (х1 , х2 , … хn ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х1 , х2 , … хn
б) область G определяется системой линейных равенств или неравенств.
Математическая модель любой задачи линейного программирования включает в себя:
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать
Алгоритм нахождения базиса системы векторов
Для того чтобы найти базис системы векторов Av А2. А , необходимо:
1) составить соответствующую системе векторов однородную систему уравнений
2) привести эту систему к равносильной разрешенной системе вида
- 3) записать базис системы векторов Б = (АрА2, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
- 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора
в разрешенной системе уравнений, т.е.
Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.
Пример 3.3. Найти ранг и базис системы векторов
разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.
Решение. Составим систему уравнений A t ay + А2х2 + . + А„хп = 0, которая в координатной записи имеет вид
Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.
Разрешенная система имеет вид
В базис системы векторов включаем 1-й и 2-й векторы Б: = (AVA2), которые соответствуют разрешенным неизвестным х1 и х2. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.
Запишем разложения векторов по базису. Коэффициентами разложения вектора А3 являются координаты вектора А’3 = (3, -2), т.е. коэффициенты при х3 в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х3 А3 = ЗЛ1 — 2Аг Аналогично, коэффициентами разложения вектора А4 являются координаты вектора А’4 = (4, 1) А4 = 4Ау + 1 Ат
Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я94 = 1.
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
| Вход Регистрация | Donate FAQ Правила Поиск |
Правила форума
Видео:Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать
Основы линейной алгебры
 |
05/12/06
126
Нижний Новгород
 |
21/12/05 |
| |||||||||||||||||||||||||||||||||||||
