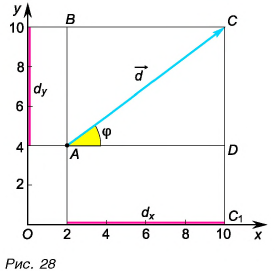
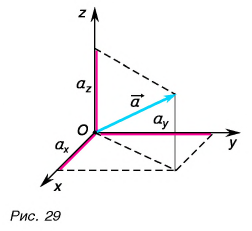
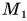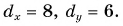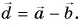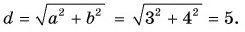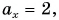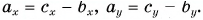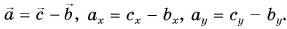Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).
Проекция вектора на ось
обозначается через al или
, а угол между осью
и вектором
будем обозначать так:
. Таким образом,
(2)
Если
— углы, образованные вектором
с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора
на координатные оси будут равны
(3)
В дальнейшем предполагается, что система координат — прямоугольная.
Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле
(4)
т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.
Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).
- Проекция вектора на ось в физике — формулы и определения с примерами
- Как определяют проекцию вектора на ось
- Можно ли найти модуль и направление вектора по его проекциям на координатные оси
- Пример №1
- Пример №2
- Проекция вектора на ось
- Как разложить вектор на проекции
- Алгоритм действий для разложения вектора на проекции
- Формулы разложения вектора на проекции
- 🌟 Видео
Видео:Угол между векторами | МатематикаСкачать

Проекция вектора на ось в физике — формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Видео:Угол между векторами. 9 класс.Скачать

Как определяют проекцию вектора на ось
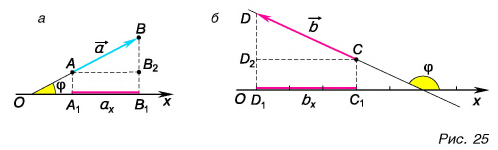
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 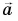
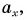
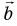
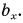
Проекция 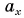
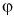
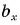
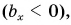
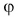
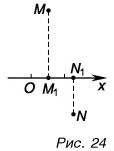
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 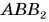
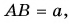
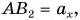
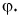
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
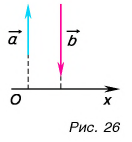
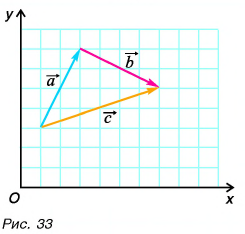
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 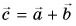
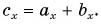
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 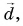
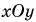
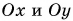
Модуль вектора 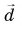
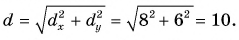
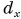
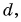
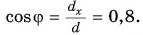
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 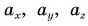
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
1. Определите сумму и разность взаимно перпендикулярных векторов 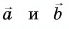
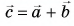
Решение
Сумму векторов 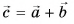
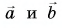
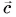
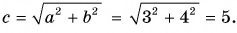
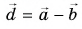
Модуль вектора 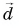
Ответ:
Пример №2
Выразите вектор 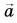
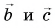
Решение
По правилу треугольника находим: 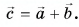
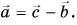
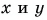
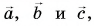
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Проекция вектора на ось
Вектор может отбрасывать тень (проекцию) на какую-нибудь ось
Если:
- вектор параллелен оси, то «его проекция = его длина», пример для вектора ( vec );
- вектор перпендикулярен оси, то его проекция равна нулю, пример для вектора ( vec );
- проекция направлена против оси, то её записывают со знаком «-», пример для вектора ( vec ).
- чем больше вектор наклоняется к оси, тем больше его проекция на эту ось. Сравните проекции векторов ( vec ) и ( vec ).
Примечание:
Длина вектора – это положительная величина, а проекция вектора может быть отрицательной
Видео:Как находить угол между векторамиСкачать

Как разложить вектор на проекции
Мы уже находили длину и направление вектора по его координатам.
Теперь решим обратную задачу: пользуясь длиной и направлением вектора, найдем его координаты.
На плоскости (две оси) легко разложить вектор на проекции, если известны:
- длина вектора и
- угол между вектором и какой-либо осью (угол обозначается дугой).
Алгоритм действий для разложения вектора на проекции
- Проводим прямоугольник так, чтобы вектор стал его диагональю.
- Диагональ разделит прямоугольник на треугольники. Эти два треугольника прямоугольные.
- Выберем треугольник, в котором угол отмечен дугой.
- Дуга одним своим концом всегда касается гипотенузы, а вторым концом – одного из катетов.
Важно! Вектор, который мы раскладываем, всегда является гипотенузой.
Формулы разложения вектора на проекции
Формулы разложения легко запомнить с помощью фразы:
Гипотенузу умножаем на косинус (угла), получаем катет, который касается (дуги).
На языке математики эта фраза запишется так:
[ |vec| cdot cos(alpha) = m_ ]
Катет ( m_ ) – это «x» координата вектора.
Если длину вектора умножим на синус, то получим второй катет:
[ |vec| cdot sin(alpha) = m_ ]
Катет ( m_ ) – это «y» координата вектора.
Обе формулы запишем в виде системы:
[ large boxed <beginleft|vecright| cdot cos(alpha) = m_ \ left|vecright| cdot sin(alpha) = m_ end> ]
Величина ( |vec| ) — это длина вектора ( vec )
🌟 Видео
Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Найти угол между лучом ОА и осью ОХ, если А(-1,1)9 класс геометрияСкачать

Урок 9. Проекции вектора на координатные осиСкачать

Построение проекции вектора на осьСкачать

найти угол между единичными векторамиСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

21. Угол между прямой и плоскостьюСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

100 Угол между векторамиСкачать

№1019. Найдите угол между лучом ОА и положительной полуосью Ох, если точка А имеет координатыСкачать

11 класс, 5 урок, Угол между векторамиСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Координаты точки и координаты вектора 1.Скачать

Косинус угла между векторами. Коллинеарность векторовСкачать