Как найти площадь четырехугольника на клетчатой бумаге 1х1

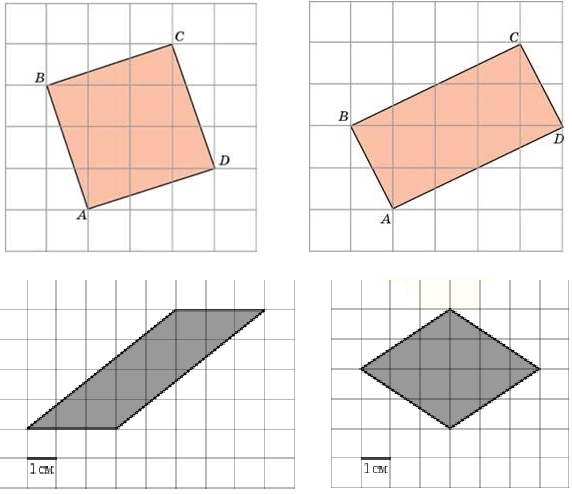
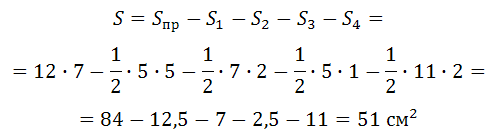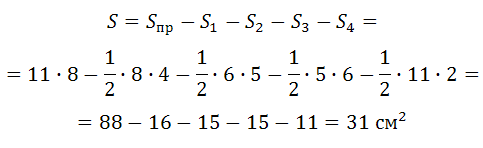Площадь четырёхугольника на клетчатой бумаге. В статье « Нахождение площади треугольник а » я обещал рассмотреть задачи на вычисление площади четырёхугольника, построенного на листе в клетку. Как вы знаете, к четырёхугольникам относятся: прямоугольник , квадрат , параллелограмм , трапеция , ромб , а также произвольный четырёхугольник (выпуклый или вогнутый).

Мы с вами рассмотрим единый подход к решению всех типов таких заданий. Вот примеры рисунков из интересующих нас задач:

Фигуры построенные на листе в клетку (1×1 см)

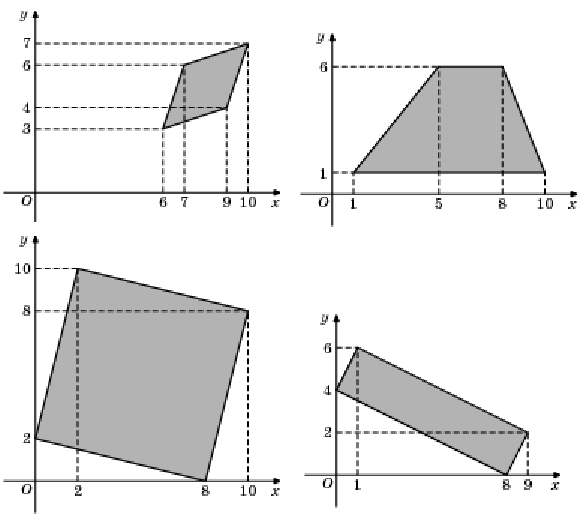
Фигуры построенные на координатной плоскости

Запомните! Вокруг любого выпуклого четырёхугольника мы можем описать прямоугольник. А далее для решения необходимо воспользоваться всего двумя формулами: площади прямоугольника и площади треугольника.

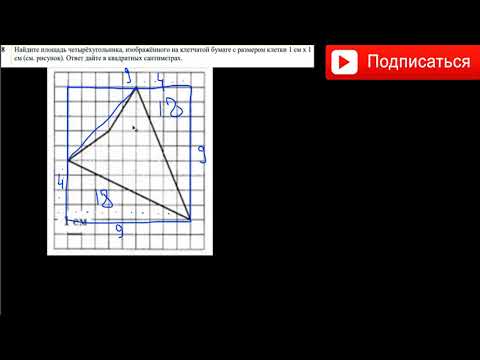
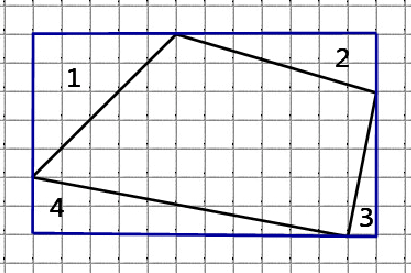
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Около данного четырёхугольника описываем прямоугольник:

Из площади построенного прямоугольника вычтем площади четырёх прямоугольных треугольников:

Рассмотрим пример вогнутого четырёхугольника:

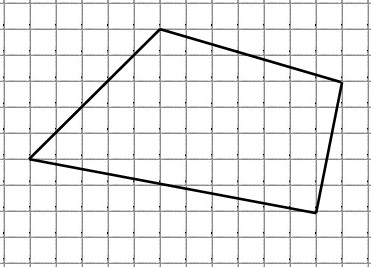
Найдите площадь четырёхугольника , изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Также описываем прямоугольник, но здесь ещё строим дополнительный отрезок, соединяющий левый верхний угол прямоугольника с вогнутым углом данного четырёхугольника:

Из площади построенного прямоугольника вычтем площади четырёх треугольников:

Если четырёхугольник задан на координатной плоскости, то его легко можно построить на листе в клетку по заданным координатам вершин и применить изложенный выше подход к решению.

Конечно, данный способ нерационален абсолютно для всех задач. Но в вашем арсенале он быть должен, и им владеть необходимо, его удобно использовать во многих задачах

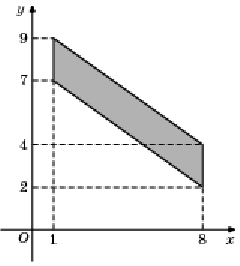
Например, для нахождения представленного четырёхугольника

целесообразно воспользоваться формулой площади параллелограмма, где основание будет равно 2, а высота 7. Но и представленным способом её также решать можно .

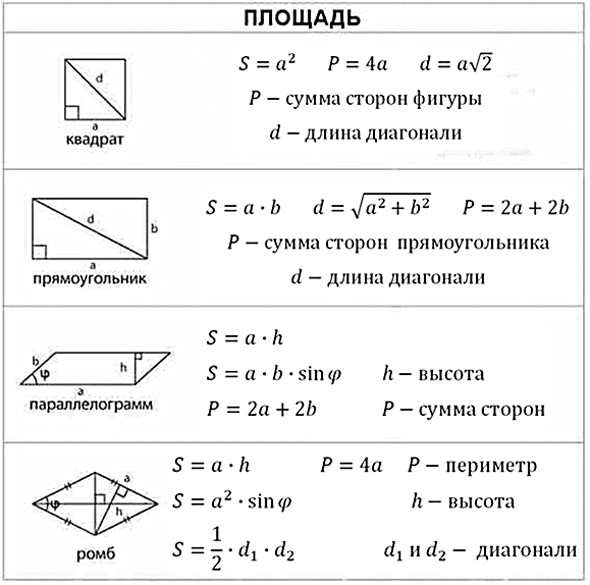
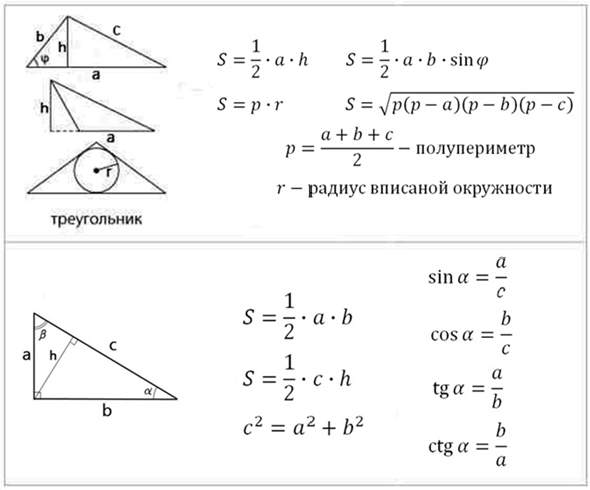
Напомню формулы площадей фигур, которые необходимо знать:

На этом всё. Надеюсь, информация была полезной. В будущем рассмотрим с вами задачи на нахождение площади круга, площади части круга и другие, где используются формулы площади круга и окружности. Также есть ещё один интересный приём, который целесообразно использовать для нахождение площади четырёхугольников вида (взяты из прототипов задач):

Видео:Самый простой способ нахождения площадиСкачать

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

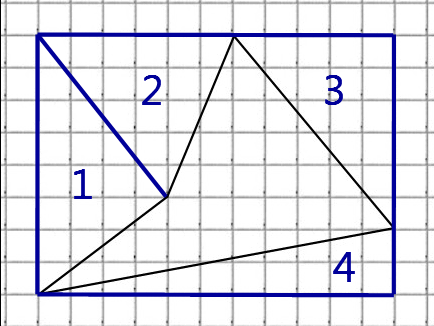
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Видео:ОГЭ по математике На клетчатой бумаге с размером 1х1 изображен параллелограммСкачать

Вычисление площади многоугольников изображённых на клетчатой бумаге.

Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

1 способ: Площадь фигур по формулам.

рис 1

S=

S = S =

2 способ: Площадь фигуры как сумма площадей её частей

Задача 1. Найдём площадь фигуры АВС D (см.рис.4). Если клетки размером 1х1см.

Разобьем фигуру АВС D на части (1, 2, 3 и 4).

о свойству площадей:

S = S 1 + S 2 + S 3 + S 4 =

= (1∙4):2 + (1∙3):2 + 1∙1 + (1∙2):2 =

2 + 1,5 + 1 + 1 = 5,5 см²

3 способ: Площадь фигуры как часть площади прямоугольника

Конечно, есть ещё способы нахождения фигур на клеточной бумаге. Например, можно просто считать количество целых клеток внутри фигуры, а из оставшихся кусочков «складывать» целые клетки, но это довольно долго и трудно, особенно если фигура сложной формы.

Задача 2. Найдём площадь фигуры АВС D (см.рис.5). Если клетки размером 1х1см.

Опишем около фигуры АВС D прямоугольник.

И

з площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2, 3 и 4):

S = S пр – S1 – S2 – S3 – S4 =

=

4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 – (3∙1):2 = 16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см ²

4 способ :Формула Пика

Есть такие фигуры на клеточной бумаге, для которых эти формулы применить очень трудно, да и эта работа занимает много времени. А на экзамене по математике в 9-м и в 11-м классе каждая минута дорога! Площади многоугольников, вершины которых расположены в узлах решетки, можно вычислять очень быстро.Есть интересная формула, которая связывает их площадь с количеством узлов, лежащих внутри и на границе данного многоугольника. Эта замечательная и простая формула называется формулой Пика. Знакомство с формулой Пика особенно актуально накануне сдачи ЕГЭ и ОГЭ. С помощью этой формулы можно без проблем решать большой класс задач, предлагаемых на экзаменах,—это задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге. Маленькая формула Пика заменит целый комплект формул, необходимых для решения таких задач. Формула Пика будет работать «одна за всех…»!

рис.6

Пусть В – число узлов решетки, расположенных строго внутри многоугольника,

Г – число узлов решетки, расположенных на его границе , включая вершины,

S — его площадь. Тогда справедлива формула Пика: S = В + – 1.

Эта формула не является секретной. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. Автор этой формулы австрийский математик Георг Пик (приложение 1). [8]

Формула Пика верна для всех рассмотренных выше примеров. Теперь мы знаем, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Рассмотрим применение формулы Пика на примерах:

Найдем площадь треугольника (см.рис.7. Отметим узлы (пересечение линий) на границе треугольника и внутри треугольника:

В = 34 (обозначены синим), Г = 15 (обозначены оранжевым).

S = 34 + 15/2 – 1 = 40,5 ед²

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. [9]

Задача 4. Найдем площадь пятиугольника

Отметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:

В = 43 (обозначены синим),

Г = 14 (обозначены оранжевым).

S = 43 + 14/2 – 1 = 49 ед²

Кто же такой Георг Александер Пик?

Австрийский математик Георг Александер Пик родился 10 августа 1859 году в Вене. Его отец, будучи руководителем частного института, предпочел до 11 лет обучать мальчика на дому, а потом отдал его сразу в четвертый класс гимназии, которую он окончил в 1875 году.

В 16 лет Георг поступил в Венский университет. В 20 лет получил право преподавать физику и математику. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. [8]

Среди всего многообразия достижений австрийского математика выделяется формула для вычисления площадей многоугольников с вершинами в узлах клетки открытая им в 1899 году. Она стала широко известна только в 1969 году, после того, как Гуго Штейнгауз включил ее в свою знаменитую книгу «Математический калейдоскоп». В Германии эта теорема включена в школьные учебники.

После выхода в 1927 году на пенсию Пик вернулся в свой родной город Вену. Однако после аншлюса (присоединение) 12 марта 1938 года Австрии с Германией ему снова пришлось перебраться в Прагу. В сентябре 1938 года фашистская Германия вторглась на территорию Чехословакии. Г.А. Пик был брошен в концентрационный лагерь в Терзинштадте, где и умер две недели спустя.

Задачи с практическим содержанием

Поможет нам формула Пика и для решения геометрических задач с практическим содержанием, когда объект изображен на клетчатой бумаге в масштабе. [4]

Задача 5. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 200 м (рис. 9).

Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + – 1

S = 8 + 7/2 – 1 = 10,5 см²

Т.к. 1 см² — 200² м², то

S массива = 40000 · 10,5 = 420 000 м²

Рис. 9 Ответ: 420

Задача 6 . Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м (рис. 10).

Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + – 1. В = 7, Г = 4.

S = 7 + 4/2 – 1 = 8 см², т.к. 1 см² — 100² м², то

S поля = 10000 · 8 = 80 000 м²

Из всех задач по геометрии у нас вызывают интерес задачи на решётках. И это не случайно. Такие задачи в учебниках по геометрии не встречаются, а на экзаменах и в олимпиадных заданиях они есть. Вот такие задачки надо научиться решать. Существует достаточное количество способов нахождения площадей фигур на клетчатой бумаге.

Мы рассмотрели основные из них. Задачи, поставленные в самом начале нашей работой, выполнили. Все предложенные способы, нахождения площадей плоских фигур, на клетчатой бумаге нам очень интересны, но самым результативным оказался способ решения по формуле Пика.

Формула Пика — это настоящий клад для тех ребят, которые не могут выучить все формулы для вычисления площадей фигур, для тех, кто так и не уяснил до конца, как разбить фигуру на части или выполнить дополнительное построение. С другой стороны, для тех, кто площадь многоугольника, изображённого на клетчатой бумаге умеет находить с помощью вышеперечисленных приёмов, а формула Пика нужна, чтобы решить задачу ещё и этим способом , тем самым проверить правильность своего предыдущего решения, сверив полученные ответы.

Анализ решений показал, что применение формулы Пика даёт возможность решать задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге очень быстро и легко. Это позволяет экономить время на экзамене Эта работа была нам интересна, и мы надеемся, что результаты наших исследований, помогут учащимся при сдаче экзамена по математике.

Георг Александр Пик ( нем. Georg Alexander Pick ; 10 августа 1859 г. – 13 июля 1942 г. ) – австрийский математик . В 16 лет Георг окончил школу и поступил в Венский университет . В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсберга Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете . Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию . Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну . Там он познакомился с другим учеником Клейна, Давидом Гильбертом . Позже, в 1885 г., он вернулся в Прагу , где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифференциальный геометрии , эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа , всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца-Пика . Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [8]

Видео:Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см.Скачать

Исследование площадей многоугольников, изображенных на клетчатой бумаге.

Найдите площадь окрашенной фигуры, изображенной на чертеже. Размер каждой клетки равен 1 см * 1 см . Ответ дайте в квадратных сантиметрах.

Дано:

🎦 Видео

САМОЕ ПОНЯТНОЕ РЕШЕНИЕ. Найдите площадь четырехугольникаСкачать

На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

ОГЭ 2019 Задание 19. Геометрия на клетчатой бумаге. Площади.Скачать

Площадь четырёхугольника на клетчатой бумагеСкачать

Формула Пика или Как найти площадь любой фигуры на клетчатой бумагеСкачать

На клетчатой бумаге с размером клетки 1 × 1 изображена ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Вычисление площадей на клетчатой бумагеСкачать

Как найти площадь фигуры#математика #площадьфигуры #геометрия #формулапика #репетиторСкачать

18 ЗАДАНИЕ ОГЭ НАЙДИТЕ ПЛОЩАДЬ ТРАПЕЦИИСкачать

Как найти площадь произвольного четырехугольника, изображенного на клетчатой бумагеСкачать

18 ЗАДАНИЕ ОГЭ НАЙТИ ПЛОЩАДЬ ТРЕУГОЛЬНИКАСкачать

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.Скачать

Вычисление площади треугольника.задача на клетчатой бумагеСкачать

На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Площадь одной клетки равна 1. Найдите площадь фигуры ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1смСкачать